Аксиоматический метод
Для древних греков объекты математики имели реальное существование в «мире идей». Некоторые свойства этих объектов представлялись умственному взору совершенно неоспоримыми и объявлялись аксиомами, другие — неочевидные — следовало доказывать, опираясь на аксиомы. При таком подходе не было большой необходимости в точной формулировке и полном перечне всех аксиом: если в доказательстве используется какое-то неоспоримое свойство объектов, то не так уж важно, занесено оно в список аксиом или нет — истинность доказываемого свойства от этого не страдает. Хотя Евклид в своих «Началах» и приводит список определений и аксиом (включая постулаты), он, как мы видели в главе 10, сплошь и рядом использует положения, интуитивно совершенно очевидные, но не входящие в число аксиом. Что же касается его определений, то число их больше, чем число определяемых объектов, и они совершенно непригодны для использования в процессе доказательства. Список определений в первой книге «Начал» начинается следующим образом.
Точка есть то, что не имеет частей. Линия есть длина без ширины. Концы линий суть точки. Прямая линия есть та, которая одинаково лежит относительно всех своих точек.И так далее, всего 34 определения. Швейцарский геометр Ж.Ламберт (1728–1777) заметил по этому поводу: «То, что Евклид предпосылает в таком изобилии опеределения, есть нечто вроде номенклатуры. Он, собственно говоря, поступает так, как поступает, например, часовщик или другой ремесленник, начиная знакомить учеников с названиями орудий своего мастерства».
Тенденция к формализации математики породила тенденцию к уточнению определений и аксиом. Уже Лейбниц обратил внимание на то, что построение Евклидом равностороннего треугольника опирается на положение, которое из определений и аксиом не вытекает (мы разбирали это построение в главе 10). Однако лишь создание неевклидовой геометрии Н.Лобачевским (1792–1856), И.Больяи (1802–1860) и К.Гауссом (1777–1855) повлекло за собой всеобщее признание аксиоматического подхода к математическим теориям как основного метода математики.
Первоначально «воображаемая» геометрия Лобачевского, как и все «воображаемые» явления в математике, была встречена с недоверием и враждебностью. Но вскоре неопровержимый факт существования этой геометрии стал менять точку зрения математиков на отношение между математической теорией и действительностью. Математик не мог отказать геометрии Лобачевского в праве на существование, ибо была доказана ее непротиворечивость. Правда, геометрия Лобачевского противоречила нашей геометрической интуиции, но при достаточно малом параметре кривизны пространства она в малых объемах пространства была неотличима от геометрии Евклида. Что же касается космических масштабов, то совершенно не очевидно, что мы можем и здесь довериться нашей интуиции, сформировавшейся под воздействием опыта, ограниченного малыми объектами. Итак, мы имеем перед собой две конкурирующие геометрии, и возникает вопрос, какая же из них «истинная»?
Стоит задуматься над этим вопросом, как становится ясным, что слово «истинная» не зря взято в кавычки. Строго говоря, эксперимент может дать ответ не на вопрос об истинности или ложности геометрии, а лишь на вопрос о ее полезности или бесполезности, а точнее, о степени полезности, ибо совсем бесполезных теорий, пожалуй, не существует. Эксперимент имеет дело не с геометрическими, а с физическими понятиями. При обращении к эксперименту мы вынуждены как-то интерпретировать геометрические объекты, например, считать, что прямые линии реализуются световыми лучами. Если мы обнаружим, что сумма углов треугольника, образованного световыми лучами, меньше 180, то это вовсе не значит, что геометрия Евклида «ложна». Быть может, она «истинна», но свет распространяется не по прямым, а по дугам окружностей или каким-либо другим кривым линиям. Выражаясь более точно, эксперимент этот покажет, что лучи света нельзя рассматривать как евклидовы прямые. Сама евклидова геометрия этим опровергнута не будет. То же относится, конечно, и к неевклидовой геометрии. Эксперимент может дать ответ на вопрос, является ли луч света воплощением прямой Евклида или прямой Лобачевского, и это, конечно, важный аргумент при выборе той или другой геометрии в качестве основы для физических теорий, но права на существование у той геометрии, которой «не повезло», он не отнимает.
Быть может, ей повезет в следующий раз, и она окажется весьма удобной для описания какого-то другого аспекта действительности.
Подобные соображения привели к переоценке относительной важности природы математических объектов и их свойств (включая отношения как свойства пар, троек и т. д. объектов). Если прежде объекты представлялись имеющими независимое реальное существование, а их свойства — чем-то вторичным и производным от природы, то теперь именно свойства объектов, зафиксированные в аксиомах, стали той основой, которая определяет специфику данной математической теории, а объекты утратили всякую специфику и вообще утратили свою «природу», т. е. связываемые с ними в обязательном порядке интуитивные представления; в аксиоматической теории объект это нечто, удовлетворяющее аксиомам. Аксиоматический подход окончательно утвердился на рубеже XIX и XX вв. Интуиция, конечно, сохранила свое значение основного (и, пожалуй, единственного) инструмента математического творчества, но окончательным результатом творчества стала считаться полностью формализованная аксиоматическая теория, которая путем интерпретации может применяться к другим математическим теориям или к неязыковой действительности.
Архимед и Аполлоний
В Александрийскую эпоху (330–200 до н. э.) живут два великих ученых, в работах которых греческая математика достигает своей высшей точки, — Архимед (287–212 до н. э.) и Аполлоний (265?–170? до н. э.). Архимед в своих геометрических трудах уже далеко выходит за пределы фигур, образованных прямыми и окружностями. Он развивает теорию конических сечений, исследует спирали. Главная заслуга Архимеда в геометрии — многочисленные теоремы о площадях, объемах и центрах тяжести фигур и тел, образованных не только прямыми линиями и не только плоскими поверхностями. Он использует «метод исчерпывания». Чтобы проиллюстрировать круг задач, решаемых Архимедом, перечислим задачи, вошедшие в его сочинение «Метод», цель которого, как это видно из заглавия, не полная сводка результатов, а освещение метода работы. «Метод» содержит решение следующих 13 задач: площадь параболического сегмента, объем шара, объем сфероида (эллипсоида вращения), объем сегмента параболоида вращения, центр тяжести сегмента параболоида вращения, центр тяжести полушария, объем сегмента шара, объем сегмента сфероида, центр тяжести сегмента шара, центр тяжести сегмента сфероида, центр тяжести сегмента гиперболоида вращения, объем сегмента цилиндра, объем пересечения двух цилиндров (последняя задача — без доказательства).
Не меньшее значение, чем работы по геометрии, имели исследования Архимеда в области механики. Он открыл свой знаменитый «закон Архимеда», занимался законами равновесия тел. Он был необыкновенно искусен в изготовлении различных механических устройств и приспособлений. Благодаря машинам, сделанным под руководством Архимеда, жители его родного города Сиракузы отразили первый штурм города римлянами. Механические соображения часто использовались Архимедом в качестве подспорья при выводе геометрических теорем. Однако было бы ошибкой полагать, что Архимед хотя бы в чем-то отклонялся от традиционного греческого образа мышления. Он считал задачу решенной только тогда, когда находил безупречное с логической точки зрения геометрическое доказательство.
Свои механические изобретения он рассматривал как забаву или же, как житейские занятия, не имеющие никакого научного значения. Плутарх пишет:
Хотя эти изобретения прославили его сверхчеловеческую мудрость, тем не менее он ничего не писал по таким вопросам, ибо полагал, что сооружение всякого рода машин и вообще всех приспособлений для практического употребления — дело низкое и неблагородное; сам же он стремился лишь к тому, что по красоте своей и совершенству находится далеко от царства необходимости.
Из всех своих достижений сам Архимед больше всего гордился доказательством того, что объем шара, вписанного в цилиндр, составляет две трети объема цилиндра. Он завешал изобразить на своей могильной плите цилиндр с вписанным в него шаром. Римский полководец Марцелл, солдат которого убил Архимеда после взятия Сиракуз, (как утверждают, вопреки распоряжению Марцелла), разрешил родственникам Архимеда выполнить завещание покойного.
Аполлоний прославился, главным образом, своей работой по теории конических сечений. Фактически эта работа — последовательное алгебраическое исследование кривых второго порядка, выраженное на геометрическом языке. В наше время все результаты, полученные Аполлонием, может легко проверить любой студент, используя методы аналитической геометрии. Но, чтобы сделать то же в рамках чисто геометрического подхода, Аполлонию потребовалось проявить чудеса математической интуиции и изобретательности.
Арифметическая алгебра
Успехи геометрии оттеснили на задний план искусство решения уравнений. Однако оно продолжало развиваться и породило арифметическую алгебру. Возникновение алгебры из арифметики — это типичный метасистемный переход. Когда ставится задача о решении уравнения — независимо от того, формулируется ли она на обычном разговорном языке или на специализированном, — это еще задача арифметическая. И когда указывается общий метод решения — на примерах, как это делается в начальной школе, или даже в виде формулы, мы все еще не выходим за пределы арифметики. Алгебра начинается тогда, когда сами уравнения становятся объектом деятельности, когда изучаются свойства уравнений и правила их преобразования. Наверно, каждый, кто помнит, как он познакомился с алгеброй в школе (если только это было на уровне понимания, а не зазубривания), помнит и то радостное чувство изумления, которое испытываешь, когда оказывается, что разнотипные арифметические задачи, приемы решения которых представлялись друг с другом совершенно не связанными, решаются путем однотипных преобразований уравнений по нескольким простым и понятным правилам. Все ранее известные методы вписываются в стройную систему, открываются новые методы, вводятся в рассмотрение новые уравнения и целые классы уравнений (закон разрастания предпоследнего уровня), появляются новые понятия, не имеющие решительно никакого смысла в рамках собственно арифметики: отрицательные, иррациональные и мнимые числа.
Принципиальной необходимости создания специализированного языка для развития алгебры нет. Однако на деле только созданием специализированного языка завершается метасистемный переход в головах людей. Специализированный язык дает возможность убедиться, что мы имеем дело с некоей новой реальностью — в данном случае с уравнениями, которые можно рассматривать как объект выкладок, подобно объектам предыдущего уровня — числам. Людям свойственно не замечать воздуха, которым они дышат, и языка, которым все время пользуются. Созданный же вновь специализированный язык выпадает из сферы естественного языка и представляется частью неязыковой действительности.
Это способствует метасистемному переходу. И, конечно, огромную роль играют практические удобства использования специализированного языка: обозримость выражений, уменьшение затрат на переписывание и т. п.
Арабский ученый Мухаммед ибн Муса ал-Хорезми (780–850) написал несколько сочинений по математике, которые в XII в. были переведены на латынь и на протяжении четырех столетий служили в Европе важнейшими учебными пособиями. Одно из них — «Арифметика» — донесло до европейцев десятичную систему счисления и правила (алгоритмы — от имени ал-Хорезми) выполнения четырех действий арифметики над числами, записанными по этой системе. Другое сочинение называлось «Книга об ал-джебр и ал-мукабала». Оно имело целью обучить искусству решения уравнений, которое необходимо, по словам автора, «в случаях наследования, раздела имущества, торговли и во всех деловых взаимоотношениях, а также при измерении земель, проведении каналов, геометрических вычислений и в других случаях...» «Ал-джебр» и «ал-мукабала» – два приема, которые ал-Хорезми использует для решения уравнений. Эти приемы он придумал не сам, они описываются и используются уже в «Арифметике» позднегреческого математика Диофанта (III в.), прославившегося своими методами решения целочисленных (диофантовых) уравнений. В той же «Арифметике» Диофанта встречаются и зачатки буквенной символики. Поэтому если считать кого-то родоначальником арифметической алгебры, то, очевидно, это будет Диофант. Однако в Европе об алгебраических приемах узнали впервые от ал-Хорезми, а труды Диофанта стали известны гораздо позже. Никакой специальной алгебраической символики, даже в зачаточном состоянии, у ал-Хорезми нет. Уравнения фигурируют в виде записи на естественном языке. Но мы для краткости опишем эти приемы и приведем пример, пользуясь современной символикой.
Ал-джебр — это перенесение вычитаемых членов из одной части уравнения в другую; ал-мукабала — вычитание из обеих частей уравнения одинакового члена. Эти приемы ал-Хорезми рассматривает как различные, ибо понятие об отрицательном числе у него отсутствует.
Возьмем для примера уравнение
7x - 11 = 5x - 3.
Применяя прием ал-джебр два раза — для вычитаемого 11 и для вычитаемого 3, получаем
7x + 3 = 5x + 11.
Теперь применим два раза прием ал-мукабала — для члена 3 и для члена 5х. Получаем
2x = 8.
Отсюда х = 4.
Итак, хотя ал-Хорезми не использует специального алгебраического языка, его книга содержит первые наметки алгебраического подхода. Европейцы по достоинству оценили этот подход и дали ему дальнейшее развитие. Само слово «алгебра» происходит от названия первого из приемов ал-Хорезми.
Арифметика с птичьего полета
Ситуации и представления в нервной системе человека моделируют смену состояний окружающей среды. Языковые объекты моделируют смену ситуаций и представлений. В результате теория является «двухэтажной» языковой моделью действительности (рис. 9.5). Схема использования теории такова. Ситуация Si кодируется языковым объектом Li. Этот объект, конечно, может состоять из множества других объектов и иметь сколь угодно сложную структуру. Объект L1 есть имя для S1. Некоторое время спустя ситуация S1 сменяется ситуацией S2. Осуществляя некоторую языковую деятельность, мы преобразуем L1 в другой объект L2, и, если наша модель правильна, L2 есть имя S2. Тогда, не зная реальной ситуации S2, мы можем получить о ней представление путем декодирования языкового объекта L2. Языковая модель определяется, очевидно, как семантикой объектов Li («материальная часть» по военной терминологии), так и видом языковой деятельности, превращающей L1 в L2.
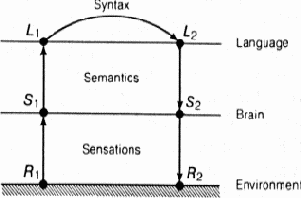
Рис. 9.5. Двухэтажная языковая модель действительности
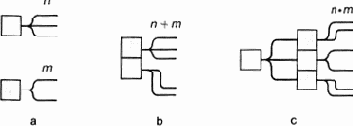
Рис. 9.6. Действия над целыми числами
Заметьте, что мы ничего не сказали о «выделении существенных сторон явления», о «причинно-следственной связи» и прочих подобных вещах, которые обычно красуются на почетных местах при описании сущности научного моделирования. И ситуация S1 у нас «не порождает» ситуацию S2, а лишь «сменяется» ею. Это, конечно, не случайно. Нарисованная нами схема логически предшествует упомянутым философским понятиям. Если у нас есть языковая модель, и лишь постольку, поскольку она у нас есть, мы можем говорить о существенных сторонах явления, об идеализации, о причинно-следственной связи и т. п. Все эти понятия, хотя они по внешности предстают как условия создания языковой модели, на самом деле являются лишь описанием в общих терминах (конечно, очень важным и нужным) уже существующих моделей. Хотя эти понятия как-будто бы «объясняют», почему вообще может существовать языковая модель, на самом деле они сами являются элементами языковой модели следующего уровня (иерархии по управлению) и исторически, конечно, появляются позже, чем первичные языковые модели (например, арифметические).
Поэтому, прежде чем использовать эти понятия, мы должны констатировать, что языковые модели вообще существуют. И на этом уровне описания нам нечего добавить к схеме на рис. 9.5. «Так бывает» — вот и все.
Как же создаются и развиваются теории? Как и все в мире, по методу проб и ошибок. Если есть отправная точка, то, начиная от нее, человек принимается сооружать языковые конструкции и исследовать, что у него получилось. Фазы конструирования и исследования постоянно сменяют друг друга: конструкция порождает исследование, исследование порождает новые конструкции.
Отправной точкой арифметики является понятие числа (целого). Аспект действительности, который отражает это понятие таков: отношение целого к его частям, способ разложения целого на части. Ту же самую мысль можно выразить и с противоположной стороны: число — способ объединения частей в целое, т. е. в некое множество (конечное). Два числа считаются тождественными, если части (элементы множества) можно поставить во взаимно однозначное соответствие; в установлении этого соответствия и состоит счет. Очевидно, однако, что одних чисел мало для теории, необходимы еще действия над ними — элементы функционирования модели, преобразования L1 > L2. Возьмем два числа n и m и представим их схематически как два способа разложения целого на части (рис. 9.6,a).
Как из этих двух чисел получить третье, т. е. третий способ разложения целого на части? Сразу приходит на ум два способа, которые можно назвать параллельным и последовательным соединением разложений. При параллельном способе оба целых образуют в качестве частей новое целое (рис. 9.6,b). Это разложение (число) мы назовем суммой двух чисел. При последовательном способе мы берем одно из разложений и каждую его часть разлагаем в соответствии с другим разложением (рис. 9.6,c). Новое число называется произведением. Оно не зависит от порядка производящих чисел. Это очень хорошо видно, если интерпретировать действия над числами не как соединение разложений, а как образование нового множества.
Сумма есть, очевидно, результат слияния двух множеств в одно (объединение множеств). Произведение имеет своим прообразом множество сочетаний любого элемента первого множества с любым элементом второго (такое множество называется в математике прямым произведением множеств). Связь этого определения с предыдущим можно проследить таким образом. Пусть первое разложение делит целое A на части a1, a2, ..., an, второе делит B на части b1, b2, …, bm. Сделав первое разложение, пометим буквами ai полученные части. Разлагая каждую часть второго на части bi сохраним первую букву и добавим вторую. Значит, на каждой части результата будет стоять aibj
и все эти сочетания будут разные. Подходы от целого к части и от части к целому дополняют друг друга. Из рис. 9.6,c легко увидеть также, что умножение можно свести к повторному сложению.
Конечно, древний человек, создавая арифметику, был далек от этих рассуждений. Но ведь и лягушка не знала, что ее нервная система должна быть устроена по иерархическому принципу! Важно, что это знаем мы.
Имея языковые объекты, изображающие числа, и умея производить над ними сложение и умножение, мы уже получаем теорию, дающую нам работающие модели действительности. Разберем простейший пример, поясняющий схему на рис. 9.5.
Пусть некий земледелец засеял пшеницей поле длиной в 60 шагов и шириной 25 шагов. Допустим, что он ожидает урожая в одну кружку пшеницы с квадратного шага. Прежде чем приступать к уборке, он хочет знать, сколько он получит кружек пшеницы. Здесь S1 — ситуация перед уборкой пшеницы, включающая, в частности, результат измерения длины и ширины поля в шагах и ожидаемую урожайность; S2 — ситуация после уборки, включающая, в частности, результат измерения количества пшеницы кружками; L1
— языковый объект 60 ×25 (знак умножения является таким же отражением ситуации S1, как числа 60 и 25: он отражает структуру множества квадратных шагов на плоскости как прямого произведения множеств линейных шагов в длину и ширину); L2 — языковый объект 1500.
Терминологическое замечание. Под теорией мы понимаем просто языковую модель действительности, дающую нечто новое по сравнению с нейронными моделями. В этом определении не учитывается, что теории могут образовывать иерархию по управлению, да этот факт и трудно отразить без введения математического аппарата. Более общие модели могут порождать более частные модели. Теорию и языковую модель мы будем считать синонимами, но все же, когда речь идет о порождении одной модели другой моделью, мы более общую будем называть теорией, а более частную — моделью.
Аристотелевская логика
Понятия, выражающие свойства ситуации в целом, мы будем называть аристотелевскими, ибо логика Аристотеля есть как раз не что иное, как последовательная теория правильного использования таких понятий. Каждому аристотелевскому понятию соответствует определенное множество ситуаций, а именно тех ситуаций, когда свойство, выражаемое этим понятием, имеет место. Поэтому аристотелевское понятие можно также описать как некое множество или класс ситуаций (явлений, объектов — в том предельно общем смысле, в котором эти термины здесь употребляются, все они равнозначны друг другу и термину «нечто», который из них самый точный, но и самый неудобный из-за необходимости считаться с грамматикой). Поэтому же все законы аристотелевской логики легко выводятся из простейших свойств операций над множествами.
Рассмотрим классический пример силлогизма.
|
Все люди смертны. |
|
Сократ — человек. |
|
Следовательно, Сократ смертен. |
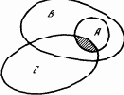
В этом рассуждении участвуют три аристотелевских понятия: «человек», «смертен» и «Сократ». Понятие «человек» характеризуется множеством ситуаций, в которых мы говорим: это — человек. То же относится и к остальным понятиям. Чтобы сделать наглядными свойства множеств, представим каждую ситуацию в виде точки внутри некоторого квадрата (рис. 6.3). Тогда этот квадрат будет олицетворять множество всех мыслимых ситуаций, что соответствует предельно общему понятию «нечто». Остальные понятия, которым соответствуют различные множества точек, будут изображаться различными областями в квадрате. Утверждение «все люди смертны», иначе говоря «каждый человек смертен», означает, что каждая точка, входящая в область «человек», входит также в область «смертен» («смертное существо»), т. е. область «человек» находится целиком в области «смертен». Точно так же вторая посылка силлогизма означает, что область «Сократ» находится целиком внутри области «человек». Отсюда следует, что область «Сократ» находится внутри области «смертен», т. е. верно утверждение «Сократ смертен».
 Нечто |
 Нечто |
На рис. 6. 4 продемонстрирована справедливость следующей схемы умозаключения (disamis по логической терминологии).
|
Все A суть B. |
|
Некоторые A суть C. |
|
Следовательно, некоторые B суть C. |
|
Иван — брат Петра. |
|
Следовательно, Петр — брат Ивана. |
Если х — брат у, то у — брат х.
Здесь буквами x и у обозначаются любые лица мужского пола. Однако такая символика выходит за пределы логики Аристотеля.
Можно ли на языке логики Аристотеля выразить этот силлогизм? Можно, если не рассматривать отдельных людей, а пары людей, точнее, упорядоченные пары, т. е. такие пары, где одному лицу приписывается номер один, а другому — номер два.
Вот этот силлогизм совершенно законный с точки зрения аристотелевской логики.
|
Пара (Иван, Петр) обладает свойством: первый — брат второго. |
|
Каждая пара, обладающая свойством: первый — брат второго, обладает свойством: второй — брат первого. |
|
Следовательно, пара (Иван, Петр) обладает свойством: второй — брат первого. |
Мы не случайно начали кибернетическое исследование понятий с аристотелевских понятий. Они проще, ибо допускают определение исключительно в терминах входных и выходных состояний, без обращения к внутренней структуре распознающей системы. Так было и в истории человеческой мысли. Сначала было осознано наличие аристотелевских понятий и только гораздо позже — отношений.
Так как в математике главное — это исследование отношений между объектами, аристотелевская логика совершенно недостаточна для выражения математических доказательств. Это было замечено давно; примеры из математики, которыми пользуется традиционная логика, говорят сами за себя, они чрезвычайно примитивны и неинтересны. До самого конца XIX в., когда началось создание новой («математической») логики, математика и логика развивались независимо.
Буквенная символика
Зачатки алгебраической буквенной символики встречаются впервые, как уже говорилось, у Диофанта. Диофант обозначал неизвестное знаком, напоминающим греческую букву ? или латинскую S. Есть предположение, что это обозначение происходит от последней буквы греческого слова ??????? — число. Были у него также сокращенные обозначения для квадрата, куба и других степеней неизвестной величины. Знака сложения не было, складываемые величины писались подряд. Знаком вычитания служило нечто вроде перевернутой греческой буквы ? знаком равенства — первая буква греческого слова ???? — равный. Все остальное выражалось в словесной форме. Известные величины всегда записывались в конкретной числовой форме, обозначений для известных, но произвольных чисел нет.
«Арифметика» Диофанта стада известна в Европе в 1463 г. С конца XV – начала XVI вв. сначала итальянские, а затем и другие европейские математики начинают пользоваться сокращенными обозначениями. Постепенно эти сокращения перекочевывают из арифметической алгебры в геометрическую — буквами начинают обозначать также неизвестные геометрические величины. В конце XVI в. француз Виет (1540–1603) делает следующий важнейший шаг — вводит буквенные обозначения для известных величин и получает тем самым возможность записывать уравнение в общем виде. Он же вводит термин «коэффициент». По внешнему виду символика Виета еще довольно далека от современной. Например, Виет пишет
|
вместо нашего |
|
К началу XVII в. ситуация в европейской математике была такова. Существовало две алгебры: первая — арифметическая, основанная на символике, созданной самими европейцами, и сделавшая существенный шаг вперед по сравнению с арифметикой древних; вторая — алгебра геометрическая — входила в состав геометрии. Она была почерпнута, как и геометрия в целом, от греков: основы — из «Начал» Евклида, дальнейшее развитие — главным образом из трудов Паппа Александрийского и Аполлония, которые к тому времени были хорошо изучены.
Ничего существенно нового в ней сделано не было. Нельзя сказать, что между этими двумя алгебрами совсем не было связи: уравнения степени выше первой могли получить только геометрическую интерпретацию, ибо где еще могли возникнуть квадраты, кубы и высшие степени неизвестного числа, как не при вычислении площадей, объемов или при манипуляциях над отрезками, связанными сложной системой пропорций. Сами названия второй и третьей степени — квадрат и куб — говорят об этом весьма красноречиво. Тем не менее, разрыв между понятиями величины и числа оставался и в полном соответствии с греческим каноном настоящим доказательством считалось только геометрическое. Когда в уравнениях появлялись геометрические объекты — длины, площади, объемы, то они выступали либо как геометрические величины, либо как именованные числа. Геометрические величины мыслились обязательно как нечто пространственное и из-за наличия несоизмеримости не сводимое к числу.
В этой обстановке и сказал свое слово один из величайших мыслителей, когда-либо живших на земле, Ренэ Декарт (1596–1650).
Цель и регулирование
Мы описали первую половину действия сложного рефлекса, которая состоит в анализе ситуации с помощью иерархии классификаторов. Бывают случаи, когда вторая — исполнительная — половина рефлекса чрезвычайно проста и сводится к возбуждению какой-то локальной группы эффекторов, например, эффекторов, активизирующих деятельность определенной железы. Именно в таких условиях поставлено большинство опытов И.П.Павлова, которые сыграли важную роль в исследовании высшей нервной деятельности животных и привели к созданию им широко известного учения о безусловных и условных рефлексах. Однако элементарные наблюдения над поведением животных в естественных условиях показывают, что оно не может быть сведено к совокупности рефлексов, которые никак не связаны между собой, а связаны только с состоянием внешней среды. Всякое сколь-нибудь сложное действие состоит из последовательности более простых действий, объединенных общей целью. Часто бывает, что отдельные компоненты в этой совокупности действий не только бесполезны, но и вредны животному, если они не сопровождаются другими компонентами. Например, чтобы прыгнуть, надо предварительно присесть, чтобы схватить добычу удобнее, надо на какое-то время ее выпустить. Две фазы действия — подготовительная и исполнительная, которые мы видим в этих примерах, — не могут явиться следствием независимых рефлексов, так как первое действие само по себе бессмысленно и, значит, такого рефлекса выработаться не могло.
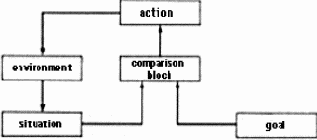
Рис. 2.6. Схема регулирования
Понятие о рефлексе при описании поведения должно быть дополнено понятием о цели и о регулировании. Схема регулирования изображена на рис. 2.6. Действие, которое предпринимает система, зависит не только от ситуации самой по себе, но также и от цели, т. е. от той ситуации, которую система стремится достигнуть. Действие системы определяется в результате сравнения ситуации и цели и направлено к устранению несоответствия между ситуацией и целью. Через блок сравнения ситуация определяет действие. Через изменение среды действие оказывает обратное влияние на ситуацию. Эта петля обратной связи является характерной чертой схемы регулирования, отличающей ее от схемы рефлекса, где ситуация просто вызывает действие.
Человек и машина
Но машинизация нижних этажей науки должна захватить и уже захватывает не только языковую деятельность, но и непосредственное манипулирование изучаемыми природными объектами. Собственно говоря, каждое исследование современной автоматики в научных экспериментах есть как раз такой «выход машины на исследование». Повышение уровня автоматизации в той или иной частной сфере исследований означает полную формализацию соответствующей части научного языка. Прообразом будущих достижений в этом направлении является, например, автоматический просмотр фотографий со следами (треками) элементарных частиц и отбор заданных конфигураций треков. Глобальный выход машин на непосредственный контакт с природой потребует глобальной формализации языка науки. Следующий этап, который можно предвидеть, — самостоятельная постановка машинами экспериментов в соответствии с метанаучными рекомендациями.
Общий смысл машинизации науки, как и машинизации производства, — это освобождение человека от нетворческой деятельности, потребность в которой, как это ни парадоксально, возникает именно благодаря успехам творческой деятельности! Ибо что такое творчество? Прежде всего, творчество — это конструктивное действие, т. е. действие, приводящее к увеличению организованности в мире. Но характеристика действия как творческого не есть характеристика по одним лишь его результатам, рассматриваемым без всякой связи с механизмом действия, с отношением между этим действием и породившей его системой. Одно и то же действие может быть творческим актом, когда оно совершается впервые, и механическим повторением пройденного, когда оно совершается по уже сложившимся, известным правилам, путем применения стандартных приемов. Все, что производится в рамках уже существующей системы управления, будь то работа вычислительной машины или сочинение трафаретных статей, — уже не творчество.
Творчество — это всегда выход за рамки системы, это свободное действие. Творчество — это метасистемный переход. Эволюция Вселенной есть непрерывное творчество.
Одно из проявлений этого процесса — творческие акты в культуре, которые создают новые уровни управления и тем самым лишают действия нижнего уровня их творческого характера. Чтобы построить пирамиду, надо было согнать тысячи рабов; чтобы рассчитать на бумаге точные положения планет, надо было выполнить тысячи арифметических действий. Машинизация призвана избавить человека от такого сорта работ и перенести его деятельность на тот уровень иерархии, где она в настоящий момент еще является творческой. Со временем и этот уровень перестанет быть творческим — граница между нетворческим и творческим трудом непрерывно ползет вверх.
В идеале должно было бы быть так, чтобы немедленно вслед за осознанием наличия системы в какой-то деятельности эта деятельность в той части, в которой она подчиняется обнаруженной системе, могла быть передана машине. Но пока это далеко не так. Существует весьма значительный разрыв между появлением нетворческой компоненты в реальной деятельности и практической возможностью передачи ее машине. Развитие автоматизации в сфере неязыковой деятельности, сопровождаемое формализацией языка в сфере языковой деятельности, сокращает этот разрыв, но он все еще остается большим.
Информационная проблема в науке, необходимость рутинных, стереотипных исследований, необходимость преодоления организационных трудностей для проведения экспериментов — все это свидетельствует о наличии этого разрыва в научной деятельности. О производственной деятельности и говорить нечего. До заводов-автоматов, которые по заложенным в них чертежам выпускали бы автомобили и телевизоры, пока еще далеко. Еще дальше до ситуации, когда никаких других заводов, кроме таких заводов-автоматов, не будет, но рано или поздно такая ситуация возникнет. Разрыв, о котором идет речь, будет ликвидирован или сведен к минимуму. Формализация языка и автоматизация избавят человека от нетворческой работы, как использование механической энергии избавило его (в массе) от тяжелой физической работы.
Человек во Вселенной
Критика теории естественных ценностей ясно показывает тот элемент научной картины мира, отправляясь от которого мы можем прийти к определенным нравственным принципам или хотя бы к определенным критериям оценки нравственных принципов. Этот элемент — учение об эволюции Вселенной и роли в ней человека. Итак, отправимся в путь.
Утверждение о непрерывном развитии — эволюции Вселенной — является важнейшей из всеобщих истин, установленных наукой. Всюду, куда только может проникнуть наш взор, мы наблюдаем необратимые изменения, подчиненные величественному общему плану, или основному закону эволюции, который проявляется как усложнение организации материи. Как часть этого плана на Земле возникает разум. И хотя нам известна ничтожная малость сферы влияния человека в космосе, мы все же считаем его венцом творения природы. Опыт исследования самых различных развивающихся систем показывает, что новое качество появляется сперва в небольшом объеме, но благодаря заключенному в нем потенциалу захватывает со временем максимум жизненного пространства и создает плацдарм для нового, еще более высокого уровня организации. Поэтому мы верим, что человечество ожидает великое будущее, превосходящее все, что только может породить самое смелое воображение.
Но ни один человек не есть человечество. Что же может человек сказать о себе самом, о месте во Вселенной своей собственной смертной личности? Что доступно человеку? Как входят его воля и его сознание в научную картину мира?
Сто лет назад картина мира, которую рисовала наука, была полностью детерминистической. Если принимать ее всерьез, можно было стать законченным фаталистом. Но теперь мы знаем, что эта картина была ошибочной. Согласно современным представлениям законы природы носят исключительно вероятностный характер. Это значит, что в мире есть нечто, что делает те или иные события более или менее вероятными (вплоть до полного запрещения), но нет ничего, что могло бы принудить события течь строго определенным образом. Законы природы таковы, что они чаще дают определенный ответ о невозможности чего-либо, чем о необходимости чего-либо, и не случайно, что наиболее общие законы носят запрещающий характер (закон сохранения энергии, закон возрастания энтропии, соотношение неопределенностей и др.).
Случаи, когда можно на длительное время вперед достаточно точно предсказать течение событий, скорее, являются исключением, нежели правилом. Сюда относятся, например, астрономические предсказания. Но ведь они возможны только потому, что здесь мы сталкиваемся с огромной разницей в масштабах времени: астрономическом и человеческом. Если подходить к движениям небесных тел с присущими им временными масштабами, то окажется, что можно сделать лишь такие же ограниченные предсказания, как по отношению к молекулам воздуха, которым мы дышим. Таким образом, успехи небесной механики, которые вдохновили Лапласа на его формулировку детерминизма, представляют собой весьма специальный случай.
Неопределенность глубоко заложена в природе вещей. Эволюция Вселенной есть непрерывное и повсеместное снятие этой неопределенности, непрерывный и повсеместный выбор одной возможности из некоторой совокупности. Мы можем сравнить две ситуации выбора, являющие собой два предельных случая и достаточно хорошо изученные нами.
Первая ситуация — столкновение элементарных частиц, являющееся объектом изучения физики. Зная начальные условия столкновения, мы можем указать вероятность тех или иных его результатов. Но и только. Если, например, вероятности отклонения налетающей частицы вверх и вниз одинаковы, то мы никак не можем предсказать, какой из этих двух случаев осуществится. И никто никогда не сможет. Это принципиально непредсказуемо.
И, однако, природа делает свой выбор. Этот акт выбора принадлежит к числу самых элементарных. Согласно современным представлениям он слеп. Сдвиги в эволюции Вселенной происходят лишь благодаря переплетению, игре бесчисленного множества подобных актов.
Вторая ситуация — волевой акт человеческой личности. Мы можем изучать этот акт извне, подобно тому, как мы изучаем столкновение частиц. Этим занимается психология в ее бихевиористической части. Зная условия, в которые поставлен человек, и какие-то его психологические свойства, мы можем сделать кое-какие предсказания — также чисто вероятностные.Но эта ситуация знакома каждому из нас и с другой точки зрения — изнутри, как наш собственный свободный выбор, как акт проявления нашей личности. Итак, то, что представляется извне как принципиальная непредсказуемость, изнутри является свободой воли.
Природа непредсказуемости в этих актах одинакова — невозможно подсмотреть за системой, не повлияв на нее, но как сильно отличаются они по своей значимости! Во-первых, волевой акт охватывает огромную по сравнению с актом рассеяния пространственно-временную область. Во-вторых, волевой акт может быть творческим актом — не слепым, косным материалом космической эволюции, а ее непосредственным выразителем, ее движущей силой.
Четыре типа языковой деятельности
Язык можно характеризовать не только степенью его формализованности, но и степенью его абстрактности, которая измеряется обилием и сложностью используемых языковых конструктов. Как мы отмечали в главе 7, правильнее было бы говорить не об абстрактности, а о «конструктности» языка, но термин этот пока не принят, поэтому мы пользуемся термином «абстрактность», который в обычном употреблении чаще обозначает именно конструктность, чем абстрактность в точном смысле слова. Язык, не использующий конструктов или использующий лишь конструкты самого низкого уровня, назовем конкретным. Язык, использующий сложные конструкты, назовем абстрактным. Деление это, хотя оно является условным и относительным, имеет, тем не менее, вполне ясный смысл. И оно не зависит от деления языков на формализованные и неформализованные — это два разных аспекта языка. Комбинируя эти аспекты, мы получаем четыре типа языков, используемых в четырех важнейших сферах языковой деятельности. Их можно расположить в следующую табличку:
|
Конкретный язык |
Абстрактный язык |
|
|
Неформализованный язык |
Искусство |
Философия |
|
Формализованный язык |
Описательные науки |
Теоретические науки (математика,…) |
Ни вертикальное, ни горизонтальное деление не является строгим, однозначным, а носит, скорее, характер количественных различий. На границах между этими «чистыми» типами языков располагаются переходные типы.
Для искусства характерен язык неформализованный и конкретный. Слова важны лишь как символы, вызывающие определенные комплексы представлений и переживаний. Эмоциональная сторона имеет, как правило, решающее значение. Однако и познавательная сторона весьма существенна; в наиболее значительных произведениях искусства эти стороны неразделимы. Основным выразительным средством является образ, который может быть синтетичен, но всегда остается конкретным.
Двигаясь по горизонтали, мы переходим от искусства к философии, которая характеризуется абстрактным неформальным мышлением. Сочетание чрезвычайной конструктности используемых понятий с незначительной степенью формализации, требующее напряженной работы интуиции, делает философский язык, без сомнения, самым трудным типом языка из всех четырех видов.
Когда искусство затрагивает абстрактные идеи, оно смыкается с философией. С другой стороны, и философия для поощрения интуиции сплошь и рядом использует художественный образ и здесь она граничит с искусством.
Перемещаясь в нашей табличке вниз, мы из области философии попадаем в область теоретических наук с языком абстрактным и формализованным. Науке вообще свойственен формализованный язык; различие между описательными и теоретическими науками заключается в различной степени использования понятий-конструктов. Язык описательной науки должен быть конкретным и точным, формализованность синтаксиса сама по себе большой роли не играет, она выступает как критерий точности семантики (логическая согласованность определений, полнота классификаций и т. п.). Модели мира, даваемые описательными науками, выражаются в терминах обыденных нейронных понятий или понятий низкой конструктности и собственно как модели они банальны и однотипны: если сделать то-то и то-то (например, поехать в Австралию, вскрыть брюшную полость лягушки и т. п.), то можно увидеть то-то и то-то. Напротив, вся суть теоретических наук в том, что они дают принципиально новые модели действительности — научные теории, основанные на понятиях--конструктах, отсутствующих на нейронном уровне. Формализованность синтаксиса играет здесь решающую роль. Предельную точку в этом квадрате нашей таблички образует математика, содержащая самые сложные конструкты и использующая полностью формализованный язык. Собственно говоря, математика — это и есть язык: формализованный язык, используемый теоретическими науками.
Перемещаясь от описательных наук вверх, мы снова оказываемся в сфере искусства. Где-то на грани между описательными науками и искусством лежит деятельность журналиста или писателя-натуралиста.
Число и величина
Во времена Пифагора и ранних пифагорейцев руководящую высоту в греческой математике занимало понятие числа. Пифагорейцы считали: Бог положил числа в основу мирового порядка. Бог — это единство, а мир — множественность. Божественная гармония в устройстве Космоса проявляется в виде числовых отношений. Немалую роль в этом убеждении сыграло открытие пифагорейцами того факта, что сочетания звуков, приятные для слуха (гармонические), создаются в том случае, когда струна укорачивается в отношениях, образуемых минимальными целыми числами: 1:2 (октава), 2:3 (квинта), 3:4 (кварта) и т. д. Числовая мистика пифагорейцев отражала их веру в то, что, в конечном счете, все закономерности природных явлений вытекают из свойств целых чисел.
Мы видим здесь проявление человеческой склонности к переоценке только что сделанных открытий. Физики конца XIX в. полагали подобно пифагорейцам, что они имеют универсальный ключ ко всем явлениям природы и что при надлежащем усердии с его помощью можно раскрыть секрет любого явления. Этот ключ — представление о пространстве, заполненном частицами и полями, которые подчиняются уравнениям Ньютона и Максвелла. Однако с открытием радиоактивности и дифракции электронов высокомерие физиков разлетелось в пух и прах.
В случае с пифагорейцами аналогичную роль сыграло открытие существования несоизмеримых
отрезков, т. е. таких отрезков, что отношение их длин не выражается никаким отношением целых чисел (рациональным числом). Не соизмеримы, например, сторона квадрата и его диагональ. Это утверждение легко доказать, опираясь на теорему Пифагора. В самом деле, допустим противное, т. е. что диагональ квадрата находится в некотором отношении m:n к его стороне. Если числа m
и n имеют общие множители, их можно сократить, поэтому будем считать, что общих множителей у m и п нет. Значит, при измерении длины некоторым единичным отрезком длина стороны есть n, а диагонали m. Из теоремы Пифагора следует, что должно иметь место равенство m2
= 2n2. Следовательно, m2 должно делиться на 2, а, следовательно, 2 должно быть в числе делителей m, т.
е. m = 2m1. Делая эту подстановку, получаем 4m12
= 2n2, т. e. 2m12 = n2. Значит, n также должно делиться на 2, что противоречит предположению об отсутствии у m и n общих множителей. На это доказательство часто ссылается Аристотель. Полагают, что оно было обнаружено еще пифагорейцами.
Если существуют величины, которые при заданном масштабе не выражаются числами, то число не может больше считаться основой основ, оно низвергается со своего пьедестала. Математикам приходится теперь пользоваться более общим понятием геометрической величины, и изучать отношения между величинами, которые иногда (скорее, в виде исключения, чем правила) могут выражаться отношением целых чисел. Такой подход лежит в основе всей греческой математики, начиная с классического периода. Соотношения, которые мы знаем как алгебраические равенства, были известны грекам в геометрической формулировке как отношения между длинами, площадями, объемами построенных определенным образом фигур.
Что мы знаем о мышлении?
Для правильного подхода к проблеме языка и мышления надо прежде всего четко отделить то, что мы знаем о мышлении, от того, что мы не знаем.
Мы знаем, что мышление — это процесс, происходящий в нервных сетях мозга. Поскольку термин «представление» у нас означает состояние какой-то подсистемы мозга, можно сказать, что мышление — это процесс изменения совокупности представлений. Но в каждый данный момент времени только какая-то (очевидно, небольшая) часть этих представлений доступна, как мы говорим, нашему сознанию. Эти представления можно объединить в одно представление (ибо несколько подсистем составляют в совокупности новую подсистему), которое есть состояние сознания в данный момент. Что такое сознание с точки зрения кибернетической, мы не знаем; есть только ряд отрывочных сведений (в частности, что сознание тесно связано с деятельностью так называемой ретикулярной формации мозга).
Итак, у мышления есть внешняя, проявляющаяся сторона — поток сознательных представлений. Этот поток поддается фиксации и изучению, из него мы пытаемся косвенным образом делать выводы о тех процессах в мозгу, которые не освещаются сознанием. Кое-что о потоке сознания мы знаем довольно твердо. Мы знаем, что в значительной степени он регулируется ассоциациями представлений, которые образуются под воздействием опыта и отражают свойства среды, в которой мы живем. В частности, благодаря ассоциации представлений мы получаем способность в той или иной степени предвидеть будущие ситуации. Мы знаем также, что человек в отличие от животных обладает способностью управлять ассоциированием, которая проявляется как воображение, кодирование, сознательное запоминание. Но мы не знаем конкретного кибернетического механизма этой способности, как, впрочем, и механизма ассоциации представлений. Эти механизмы не даны нам также и субъективно; в потоке сознания мы наблюдаем лишь их проявление, результат их действия. Наконец, субъективно нам дано ощущение свободы выбора своих поступков — свободы воли. Свобода воли проявляется и в мышлении. Мы можем по желанию переключать мысли, думать о том или ином предмете. Кибернетического истолкования свободы воли мы также не знаем, и здесь дело обстоит, пожалуй, хуже всего.
Что сделал Декарт?
Роль Декарта как философа общепризнанна. Но, говоря о Декарте как о математике, обычно указывают, что он «усовершенствовал алгебраические обозначения и создал аналитическую геометрию». Иногда к этому добавляют, что примерно в то же самое время основные положения аналитической геометрии были выдвинуты независимо от Декарта его соотечественником Пьером Ферма (1601–1665), а что касается алгебраической символики, то ее уже вовсю использовал Виет. Выходит, что в области математики Декарту особенно похвастаться нечем, и, действительно, далеко не все авторы, пишущие об истории математики, отдают ему должное. Между тем Декарт произвел революцию в математике, он создал нечто несравненно большее, чем аналитическая геометрия (понимаемая как теория кривых на плоскости), а именно: новый подход к описанию явлений действительности — современный математический язык.
Иногда говорят, что Декарт «свел геометрию к алгебре», понимая под алгеброй, конечно, алгебру числовую, арифметическую. Это грубая ошибка. Верно, что Декарт преодолел пропасть между величиной и числом, между геометрией и арифметикой, но достиг он этого не сведением одного языка к другому, а созданием нового языка — языка алгебры. По синтаксису новый язык совпадает с арифметической алгеброй, но по семантике — с геометрической. Символы в языке Декарта обозначают не числа и не величины, а отношения величин. В этом — вся суть переворота, произведенного Декартом.
Современный читатель, пожалуй, недоуменно пожмет плечами: какая разница? Неужели этот логический нюанс мог иметь серьезное значение? Оказывается, мог. Именно этот нюанс помешал грекам сделать следующий шаг в своей математике.
Мы настолько привыкли ставить иррациональные числа на одну доску с рациональными, что перестали отдавать себе отчет в том, какое глубокое различие лежит между ними. Мы пишем v2 точно так же, как пишем 4/5, и называем v2 числом, а когда нужно, заменяем на приближенное значение, и мы никак не можем понять, почему древние греки так болезненно реагировали на несоизмеримость отрезков.
Но если немного подумать, то нельзя не согласиться с греками, что v2 — это не число. Его можно представить как бесконечный процесс, порождающий последовательные знаки разложения в десятичную дробь. Можно представить его также в виде сечения в области рациональных чисел, т. е. как некое правило, которое делит все рациональные числа на два класса: те, которые меньше v2 и которые больше v2. В данном случае правило весьма простое: рациональное число a относится к первому классу, если a2
< 2 и ко второму — в противном случае. Можно, наконец, представить v2 в виде отношения между двумя отрезками; в данном случае — между диагональю квадрата и его стороной. Эти представления эквивалентны между собой, но никак не эквивалентны представлению о целом или дробном числе.
Значит ли это, что мы совершаем ошибку или нестрогость, обращаясь с корнем из двух как с числом? Отнюдь нет. Цель математики — создание языковых моделей действительности, и хороши все средства, ведущие к этой цели. Почему бы нашему языку наряду со знаками типа 4/5 не содержать и знаки типа v2? «Мой язык — что хочу, то и делаю». Важно только, чтобы мы умели интерпретировать эти знаки и совершать над ними языковые преобразования. Но интерпретировать v2 мы умеем. В практических вычислениях основой интерпретации может служить первое из приведенных выше представлений, в геометрической теории — третье. Умеем мы и производить выкладки с ними.
Теперь осталось только уточнить терминологию. Условимся то, что мы раньше называли числами, называть рациональными числами, новые объекты называть иррациональными числами, а просто числами (действительными
числами по современной математической терминологии) называть и те и другие.
Итак, в конечном счете никакой принципиальной разницы между v2 и 4/5
нет и мы оказались мудрее греков. Эту мудрость протаскивали контрабандой все те, кто оперировал со знаком v2 как с числом, признавая вместе с тем, что оно «иррационально». Обосновал и узаконил эту мудрость Декарт.
Что такое математика?
Для нас математика — это прежде всего язык, позволяющий создавать определенного рода модели действительности — математические модели. Как и в любом другом языке (или ответвлении языка), языковые объекты математики — математические объекты — суть материальные предметы, фиксирующие определенные функциональные единицы — математические понятия. Когда мы говорим, что объекты «фиксируют функциональные единицы», мы понимаем под этим, что человек, используя распознающие способности своего мозга, совершает над этими объектами или в связи с ними определенную языковую деятельность. Ясно, что не конкретный вид (форма, вес, запах) математического объекта играет роль в математике, а именно языковая деятельность, с ним связанная. Поэтому термины «математический объект» и «математическое понятие» часто употребляют как синонимы. Языковая деятельность в математике естественным образом распадается на две части: установление связи между математическими объектами и неязыковой реальностью (эта деятельность определяет семантику математических понятий) и преобразования внутри языка — математические выкладки и доказательства. Математической деятельностью обычно называют только вторую часть, а первую называют приложением математики.
Точки, линии, прямоугольные треугольники и прочее — все это математические объекты, это предметы, которые образуют наши геометрические чертежи или стереометрические модели: пятна краски, шарики из пластилина, проволочки, куски картона и т. п. Семантика этих объектов известна: точка, например, это объект, размерами и формой которого можно пренебречь. Таким образом, «точка» — это просто абстрактное понятие, характеризующее отношение объекта к его окружению. В некоторых случаях мы всю нашу планету рассматриваем как точку. Но когда мы строим математическую (геометрическую) модель, мы обычно наносим на бумагу маленькое пятнышко краски и говорим: «пусть дана точка A». Это пятнышко краски и есть языковый объект Li, а планета Земля может оказаться в роли соответствующего объекта Ri.
Никаких других, «настоящих» или «идеальных», т. е. не имеющих размеров, точек нет. Часто говорят, что «настоящих» точек нет в природе, но они существуют в нашем воображении. Это ходячее высказывание либо абсолютно бессмысленно, либо ложно — в зависимости от того, как его толковать. В любом случае оно приносит вред, так как затемняет суть дела. Никаких «настоящих» точек в нашем воображении нет и быть не может. Когда мы говорим, что представляем себе точку, мы просто представляем очень маленький предмет. Можно вообразить только то, что можно составить из данных чувственного опыта. Да и то далеко не все. Число тысяча, например, вообразить нельзя. И большие числа, и идеальные точки, и линии существуют не в нашем воображении, а в нашем языке — как языковые объекты, с которыми мы обращаемся определенным образом. В этих правилах обращения и проявляется сущность математических понятий, в частности «настояшесть» точки: размеры точек на чертеже не влияют на ход доказательства, а если надо поставить две точки так близко, что они сольются в одну, мы можем увеличить масштаб.
Но разве не свойственна утверждениям математики абсолютная точность и достоверность, резко отличающая их от содержания эмпирического знания, по преимуществу приблизительного и гипотетического? Путем измерения мы можем обнаружить, что два отрезка примерно равны, но никогда, что они равны в точности; такие утверждения — привилегия математики. На основании многовекового опыта человечества мы каждый вечер после захода Солнца можем предсказать, что завтра рано утром оно взойдет вновь. Но это предсказание — всего лишь гипотеза, хотя и весьма вероятная. Не исключена возможность, что где-то в недрах Солнца или вне его назревает космическая катастрофа неизвестной природы, в результате которой Солнце погаснет или развалится на части. Когда же мы говорим, что если к двум прибавить два, то будет четыре, или что уравнение x2 = 2 не имеет рациональных решений, мы убеждены, что эти предсказания абсолютно достоверны и будут верны всегда и всюду, если даже не только Солнце, но и вся Галактика развалится на кусочки.Мы просто не можем представить себе, чтобы было иначе. Существует, следовательно, различие между математическими моделями действительности и другими моделями, составляющими содержание нашего житейского опыта и естественных наук. Какова же природа этого различия?
Декарт и Ферма
Очень поучительно сравнить математические работы Декарта и Ферма. Как математик Ферма был не менее, а, пожалуй, более одаренным, чем Декарт. Это видно из его замечательных работ по теории чисел. Но он был восхищенным поклонником греков и продолжателем их традиций. Свои открытия по теории чисел Ферма изложил в замечаниях на полях «Арифметики» Диофанта. Его работы по геометрии возникли в результате усилий доказать некоторые положения, на которые Папп ссылался как на принадлежащие Аполлонию, не приводя, однако, доказательства. Размышляя над этими проблемами, Ферма стал систематически использовать представление положения точки на плоскости длинами двух отрезков — абсциссы и ординаты и представление кривой в виде уравнения, связывающего эти отрезки. Идея эта с геометрической точки зрения отнюдь не была новой: она является стержневой не только у Аполлония, но уже у Архимеда и восходит к еще более древним авторам. Архимед описывает конические сечения через их «симптомы», т. е. пропорции, связывающие абсциссы и ординаты точек. Возьмем, например, эллипс с большой осью AB (рис. 11.3). Перпендикуляр PQ, опущенный из некоторой точки эллипса Р на ось AB, называется «ординатой», а отрезки AQ и QB — «абсциссами» этой точки (оба термина — латинские переводы греческих терминов Архимеда). Отношение площади квадрата, построенного на ординате, к площади прямоугольника, построенного на двух абсциссах, одинаково для всех точек Р, лежащих на эллипсе. Это и есть «симптом» эллипса, т. е. по существу уравнение. Его можно записать в виде
y2 : (x1 × x2) = const.
Аналогичные симптомы устанавливаются для гиперболы и параболы. Чем это не система координат?
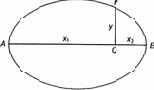
Рис. 11.3. Ордината и абсциссы эллипса
Ферма в отличие от древних формулирует симптомы не в виде словесно описанных пропорций, а в виде уравнений на языке Виета. Это облегчает преобразования; в частности, сразу видно, что вместо двух абсцисс удобнее оставить одну. Но подход остается чисто геометрическим, пространственным.
Ферма изложил свои идеи в трактате «Введение в изучение плоских и телесных мест».
Он был опубликован только в 1679 г. уже после смерти автора, но стал известен французским математикам еще в 30-х годах, несколько раньше, чем математические работы Декарта.
Знаменитая «Геометрия» Декарта вышла в свет в 1637 г. Никакого влияния со стороны Ферма Декарт, конечно, не испытал (неизвестно даже, читал ли он трактат Ферма); метод Декарта сложился задолго до выхода «Геометрии», еще в 20-х годах. Тем не менее, собственно геометрические идеи Декарта и Ферма практически тождественны. Но Декарт создал новую алгебру, основанную на понятии отношения геометрических величин. У Виета можно складывать и вычитать только однородные величины и в коэффициенты обязательно включается указание на их геометрическую природу. Например, уравнение, которое мы записали бы в виде
A3 + BA = D,
Виет записывал так:
A cubus +B planum in A aequatur D solido,
т. е. к кубу с ребром A прибавить площадь B, помноженную на A, равно объему D. Виет и Ферма идейно находятся в плену геометрической алгебры греков. Декарт решительно порывает с ней. Отношения, с которыми имеет дело алгебра Декарта, не геометрические пространственные объекты, а умозрительные понятия — «числа». Он не стеснен требованием однородности слагаемых и вообще требованием пространственной интерпретации; возведение в степень он понимает как многократное умножение и указывает число множителей маленькой цифрой выше и правее переменной. Символика Декарта практически совпадает с современной.
Диалектика Гегеля
В философии решающий удар аристотелевской логике нанес Гегель. Он показал своей диалектикой, что мир надо рассматривать не как совокупность объектов, обладающих некоторыми свойствами, а как совокупность объектов, находящихся в некоторых отношениях друг к другу. При этом свойства не исключаются, конечно, из рассмотрения, ибо понятие отношения является более общим, чем понятие свойства. Отношение может быть определено для произвольного числа объектов. В частности, число объектов может быть равно единице; такое отношение и есть свойство. Наиболее ясными интуитивно и в то же время наиболее важными являются парные отношения, т. е. отношения между двумя объектами. Два — минимальное число объектов при котором отношение перестает быть свойством и становится собственно отношением. Число два лежит в основе гегелевского метода что отражено в самом термине «диалектика».
Важнейшие черты диалектики Гегеля непосредственно вытекают из описания явлений в терминах отношений, а не свойств. Из такого подхода прежде всего следует учение о взаимодействии, взаимосвязанности всего сущего. Далее. Если два элемента находятся в соответствии, не противоречат друг другу, то они выступают как нечто целое и на первый план выходят их общие свойства, а взаимодействие, отношение между ними, отступает на второе место. Отношения между элементами, объектами проявляются постольку, поскольку они являются отношениями противоположности, противоречия, борьбы. Поэтому представление о борьбе противоположностей играет у Гегеля такую важную роль.
Рассматривая отношения между состоянием объекта в данный момент и состоянием этого же объекта в какой-то другой момент времени, мы приходим к понятию изменения. Изменение — это отношение между объектами, разделенными временным интервалом. На языке, оперирующем только со свойствами, но не с отношениями, изменение невыразимо. Самое большее, на что способен такой язык, это изобразить ряд никак не связанных друг с другом состояний объекта. Блестящим выражением этой неспособности является известная апория Зенона о летящей стреле.
Рассмотрим летящую стрелу. Возьмем определенный момент времени. В этот момент стрела занимает определенное положение в пространстве. Возьмем другой момент времени. Стрела опять занимает вполне определенное положение в пространстве. То же относится и к любому другому моменту времени. Значит, стрела всегда занимает определенное положение в пространстве. Значит, она всегда на месте.
В аристотелевских понятиях мир представляется чем-то статическим, застывшим или, в лучшем случае, механически размноженным с некоторыми вариациями. Диалектика, напротив, сделав своим предметом исследование отношений, изучает вещи с точки зрения их изменения, движения, развития. Она вскрывает историческую обусловленность и относительность (от слова «отношения»!) вещей, которые при описании в аристотелевских понятиях представляются безусловными и вечными. Комбинация понятия противоположности с понятием отношения между состояниями в последовательные моменты времени порождает понятие об отрицании и отрицании отрицания. Диалектика динамична и революционна.
По отношению к аристотелевской логике диалектика Гегеля выступила в качестве разрушительной силы, и не только по причине своей «общей» революционности, а еще и потому, что она указала на множество противоречий, которые возникают, когда описание явлений, которое требует языка отношений, втискивается в узкие рамки языка свойств. У Гегеля и его последователей эти противоречия окружались зачастую неким ореолом возвышенности и, можно сказать, полумистической значительности. Здесь сказалось, с одной стороны, идеалистическая направленность философии Гегеля, а с другой — то общее свойство новых учений, теорий, движений, что на начальных этапах своего развития они, стараясь высвободиться из рамок старого, предпочитают парадоксальную, преувеличенную форму, приобретают героический, романтический характер. Диалектика Гегеля — это героическая эпоха новой логики, когда старый логический формализм был сломан, а новый еще не создан, и поэтому противоречивым и не поддающимся формализации («диалектическим») казалось даже то, что впоследствии оказалось прекрасно упорядоченным и формализованным.
Современному мышлению, свободно пользующемуся языком отношений и вооруженному анализом логических понятий и конструкций, гегелевский стиль мышления представляется темным мудрствованием по поводу ясных вещей. Следующее рассуждение представляет собой грубо упрощенную, карикатурную схему гегелевского диалектического противоречия, показывающую, откуда это противоречие возникает.
Поставим вопрос: является ли число 1000 большим или маленьким? Оно большое, так как оно больше единицы. Оно маленькое, так как оно много меньше миллиона. Значит, оно и большое и небольшое одновременно. Диалектическое противоречие. Большое есть и в то же время небольшое, A есть не A.
Понятия «большое» и «маленькое» рассматривались здесь как свойства объектов (чисел). На самом же деле это не свойства, а замаскированные (с помощью грамматической категории прилагательного) отношения. Точный смысл можно вложить только в понятия «больше» и «меньше». Если с этой точки зрения разобрать приведенное выше рассуждение, то оно окажется просто бессмысленным. Эта карикатура направлена не против Гегеля — его заслуги в создании новой логики неоспоримы, а против тех, кто некритически относится к диалектическому методу Гегеля и во второй половине XX в. пропагандирует образ мышления первой половины XIX в., игнорируя огромный прогресс, достигнутый логикой за полтора столетия.
Дикость и цивилизация
В развитии культуры мы усматриваем прежде всего две четко различающиеся ступени: дикость (первобытная культура) и цивилизация. Четкость различия между ними не означает полного отсутствия переходных форм: переход от дикости к цивилизации не совершается, конечно, мгновенно. Но, раз начавшись, развитие культуры по пути создания цивилизации происходит так быстро, что очевидное и бесспорное отличие нового уровня культуры от старого проявляется за время, несравненно меньшее, чем время существования в состоянии дикости. Возникновение цивилизации носит характер качественного скачка. Все время существования цивилизации на Земле (не более 5 – 6 тыс. лет) составляет небольшую часть от того времени (не менее 40 тыс. лет), в течение которого человечество существует как неизменный в биологическом отношении вид. Таким образом, возникновение цивилизации — это явление, целиком принадлежащее к сфере культуры и никак не связанное с биологическим совершенствованием человека, что отличает его от возникновения языка и трудовой деятельности. Между тем последствия этого явления для биосферы поистине огромны, если даже измерять их не сложностью возникших структур, а простыми количественными показателями. За короткое время существования цивилизации человек в несравненно большей степени повлиял на облик планеты, чем за многие тысячелетия дикости. Особенно бурно растет численность человечества и его влияние на биосферу в течение последних трех столетий (срок совсем уж ничтожный), что является следствием успехов науки — любимого детища цивилизации.
Этот факт требует объяснения. Такой резкий качественный скачок в наблюдаемых проявлениях культуры должен быть связан с каким-то существенным, принципиальным изменением в ее внутренней структуре. Стержнем культуры, обеспечивающим ее единство, ее «нервной системой» является язык. Мы имеем в виду здесь не язык как абстрактную систему выражения мысли, обладающую теми или иными грамматическими особенностями, а язык как живую действительность, как общественную норму языковой деятельности.
Иначе говоря, мы имеем в виду всю наблюдаемую (материальную, если угодно) сторону мышления. Поэтому, говоря «язык», мы тут же добавляем «и мышление». Итак, язык (и мышление) — нервная система культуры, поэтому можно ожидать, что существует какое-то важное различие между языком и мышлением первобытных народов и народов, живущих в условиях современной цивилизации. И действительно, изучение культуры отсталых народов обнаруживает у них образ мышления, во многом отличный от образа мышления современного европейца. Это отличие отнюдь не исчерпывается различным уровнем знаний. Если поместить европейца в условия первобытной жизни, то вряд ли он сумеет использовать (и даже проявить!) свое знание закона Ома, или химической формулы воды, или того факта, что Земля вращается вокруг Солнца, а не наоборот. Но различие в образе мышления, в подходе к явлениям действительности останется и немедленно проявится в поведении.
Можно следующим образом суммировать отличие первобытного мышления от современного.
Первобытному человеку мир представляется наполненным всевозможными невидимыми сущностями, духами, которые выступают как причины явлений; чтобы задобрить или изгнать духов, существуют заклинания, ритуальные танцы, жертвоприношения, строго соблюдаемые запреты (табу) и т. п. Один из основоположников научного изучения первобытных культур Э. Тейлор дал этому воззрению наименование анимизма — одушевления всех предметов. Между различными предметами могут существовать, согласно представлению первобытных людей, некие таинственные связи и влияния («мистическое сопричастие» по терминологии французского этнографа Л.Леви-Брюля). Такие связи всегда существуют, в частности, между предметом и его изображением или именем. Отсюда — первобытная магия и вера в мистическую связь племени с определенным видом животных (тотем).
Но что больше всего поражает европейца, это не само содержание представлений первобытных людей, а их крайняя устойчивость, нечувствительность к данным опыта. Первобытное мышление невероятно консервативно и замкнуто.
Очевидные факты, которые, по мнению европейца, должны были неизбежно изменить представления первобытного человека, заставить его пересмотреть какие-то убеждения, не оказывают почему-то на него никакого действия. А попытки убеждать и доказывать приводят зачастую к результатам, диаметрально противоположным тем, которые ожидались. Именно в этом, а не в вере в существование духов и мистической связи между предметами состоит наиболее глубокое отличие первобытного мышления от современного. В конце концов, все в мире действительно взаимосвязано! Излагая закон всемирного тяготения, мы могли бы говорить, что в каждом теле сидит дух тяготения, и каждый дух стремится приблизиться к другому духу силой, пропорциональной массам двух тел и обратно пропорциональной квадрату расстояния между ними. Это нисколько не помешало бы нам правильно рассчитывать движение планет. Впрочем, если мы не пользуемся словом «дух», мы пользуемся словом «сила». А что такое, в сущности, сила ньютоновского притяжения? Тот же дух: нечто невидимое, неслышимое, неосязаемое, не имеющее вкуса и запаха, но, тем не менее, реально существующее и оказывающее воздействие на вещи.
Указанные особенности мышления первобытных людей обладают поразительной общностью. Можно сказать, что они общи всем без исключения первобытным народам, независимо от их расовой принадлежности и географических условий и несмотря на разнообразие конкретных форм культуры, в которых они проявляются. Это и дает основания говорить о первобытном мышлении, противопоставляя его современному мышлению и рассматривая как первую и исторически неизбежную фазу человеческого мышления. Разумеется, как и при всяком членении непрерывного процесса на отдельные фазы, существуют и переходные формы: в мышлении современного цивилизованного человека мы нередко усматриваем черты, восходящие к интеллектуальной деятельности охотников за мамонтами и пещерными медведями. Но это не уменьшает законности разделения на фазы и попыток объяснить переход от одной фазы к другой.
Итак, в чем основа различия между двумя фазами мышления: первобытной и современной?
Дискретные и непрерывные системы
Состояние системы определяется через совокупность состояний всех ее подсистем, т. е. в конечном счете элементарных подсистем. Элементарные подсистемы бывают двух типов: с конечным и бесконечным числом возможных состояний. Подсистемы первого типа называют также подсистемами с дискретными состояниями, второго типа — с непрерывными состояниями. Примером подсистемы с дискретными состояниями может служить колесико арифмометра или счетчика в такси. Нормально это колесико находится в одном из десяти положений, соответствующих десяти цифрам от 0 до 9. Время от времени оно поворачивается и переходит из одного состояния в другое. Этот процесс поворота нас мало интересует. Правильная работа системы (арифмометра, счетчика) зависит только от того, как связаны между собой «нормальные» положения колесиков, а как происходит переход из одного положения (состояния) в другое — несущественно. Поэтому мы и можем рассматривать арифмометр как систему, элементарные подсистемы которой могут находиться только в дискретных состояниях. Современная быстродействующая цифровая вычислительная машина также состоит из подсистем (триггерных схем) с дискретными состояниями. Все, что мы знаем в настоящее время о нервной системе животных и человека, указывает на то, что решающую роль в ее работе играет взаимодействие подсистем (нейронов) с дискретными состояниями.
С другой стороны, человек, катящийся на велосипеде, или аналогичная вычислительная машина дают нам примеры систем, которые описываются как состоящие из подсистем с непрерывными состояниями. В случае велосипедиста таковыми являются все движущиеся друг относительно друга части велосипеда и человеческого тела: колеса, педали, руль, ноги, руки и т. д. Их состояния — это их положения в пространстве, описывающиеся координатами (числами), которые могут принимать непрерывные множества значений.
Если система состоит исключительно из подсистем с дискретными состояниями, то и сама она может находиться лишь в конечном числе состояний, т. е. является системой с дискретными состояниями.
Такие системы мы будем называть просто дискретными
системами, а системы с непрерывным множеством состояний — непрерывными. Дискретные системы во многих отношениях проще для анализа, чем непрерывные. В частности, пересчет числа возможных состояний системы, который играет важную роль в кибернетике, требует в дискретном случае лишь знания элементарной арифметики. Пусть дискретная система A состоит из двух подсистем a1
и a2, причем подсистема a1 может иметь n2, а подсистема a2 — n2 возможных состояний. Допуская, что каждое состояние системы a1 может сочетаться с каждым состоянием системы a2, мы находим, что число N
возможных состояний системы A есть n1n2. Если система A состоит из m подсистем ai, где i
= 1, 2, ..., m, то
N = n1n2...nm.
В дальнейшем мы будем рассматривать только дискретные системы. Кроме того прагматического соображения, что они принципиально проще, чем непрерывные системы, существует еще два довода в пользу целесообразности такого ограничения.
Во-первых, все непрерывные системы можно, в принципе, рассматривать как дискретные системы с чрезвычайно большим числом состояний. В свете тех знаний, которые дала нам квантовая физика, такой подход даже следует рассматривать как теоретически более правильный. Причина, по которой непрерывные системы все же не исчезают из кибернетики, — это наличие весьма совершенного аппарата — математического анализа и, в первую очередь, дифференциальных уравнений для рассмотрения таких систем.
Во-вторых, самые сложные кибернетические системы, как возникшие естественным путем, так и созданные руками человека, неизменно оказываются дискретными. Особенно наглядно это видно на примере животных. Относительно простые биохимические механизмы, регулирующие температуру тела, содержание в крови различных веществ и т. п., являются непрерывными, но нервная система устроена по дискретному принципу.
Доказательство
Ни в египетских, ни в вавилонских текстах мы не находим ничего, что хотя бы отдаленно было похоже на математическое доказательство. Понятие о доказательстве ввели греки, и это является их величайшей заслугой. Какими-то наводящими соображениями при получении новой формулы люди, очевидно, пользовались и раньше, мы даже приводили пример грубо неверной формулы (для площади неправильных четырехугольников у египтян), явно полученной из внешне правдоподобных «общих соображений». Но только греки стали относиться к этим наводящим соображениям с той серьезностью, которой они заслуживают, стали анализировать эти соображения с точки зрения их убедительности и ввели принцип, согласно которому каждое утверждение, касающееся чисел и фигур (формула), за исключением лишь небольшого числа, должно быть доказано, выведено убедительным, не допускающим сомнений образом из этих «совершенно очевидных» истин. Неудивительно, что именно греки с их демократическим общественным строем создали учение о математическом доказательстве. Споры и доказательство играли важнейшую роль в жизни граждан греческого города-государства (полиса). Понятие о доказательстве уже существовало, оно было общественно значимой реальностью. Осталось только перенести его в область математики, что и было сделано, едва греки познакомились с достижениями древних восточных цивилизаций. Сыграло здесь роль, надо полагать, и то положение молодого любознательного ученика, в котором оказались греки по отношению к египтянам и вавилонянам — своим старшим и не всегда согласным друг с другом учителям. В самом деле, вавилоняне определяют площадь круга по формуле 3r2, а египтяне по формуле (8/9 2r)2 . Где же истина? Здесь есть о чем подумать и поспорить.
Творцы египетской и вавилонской математики остались безымянными. Греки сохранили имена своих мудрецов. Первое из них — имя Фалеса Милетского — является также первым именем, вошедшим в историю науки. Фалес жил в VI в. до н. э. в городе Милете на Малоазиатском побережье Эгейского моря.
Одна дата из его жизни установлена твердо: в 585 г. до н. э. он предсказал солнечное затмение. Этот факт, кстати, неоспоримо свидетельствует о знакомстве Фалеса с культурой древних цивилизаций, ибо, чтобы установить периодичность затмений, необходим опыт десятков и сотен лет. Так как у Фалеса не было греческих предшественников, он мог заимствовать свои познания по астрономии только у ученых Востока.
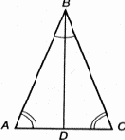
Рис. 10.1. Равнобедренный треугольник
Фалес, как утверждают греки, дал миру первые математические доказательства. В числе доказанных им положений (теорем) называют следующие:
Диаметр делит круг на две равные части.
Углы при основании равнобедренного треугольника равны.
Два треугольника, у которых одинаковы стороны и прилежащие к ней углы, равны.
Кроме того, он первый дал построение круга, описанного вокруг прямоугольного треугольника (и в честь этого открытия, как говорят, принес в жертву быка).
Простейший характер указанных теорем, их интуитивная очевидность показывают, что Фалес полностью осознавал значение доказательства как такового. Эти теоремы, явно доказывались не потому, что были сомнения в их истинности, а с целью положить начало систематическому нахождению доказательств, разработать технику доказательства. Имея такую цель, естественно начинать с доказательства самых простых предложений.
Пусть треугольник ABC равнобедренный (рис. 10.1), т. е. сторона AB равна стороне BC. Разделим угол ABC линией BD на две равные части. Перегнем мысленно наш чертеж по линии BD. Так как угол ABD равен CBD, линия BA ляжет на линию BC, а так как длины отрезков AB и BC равны, точка A ляжет на точку C. Поскольку точка D остается на месте, углы BCD и BAD должны быть равны. Если раньше нам только казалось, что углы BCD и BAD одинаковы (так, вероятно, говорил своим согражданам Фалес), то теперь мы доказали, что эти углы необходимо и с абсолютной точностью должны быть равны (тогда говорили «подобны») друг другу, т. е. совмещаться при наложении.
Задача на построение более сложна, здесь результат совсем не очевиден заранее.
Нарисуем прямоугольный треугольник (рис. 10.2). Можно ли провести окружность так, чтобы все три вершины треугольника оказались за ней? И как это сделать? Неясно. Но допустим, что интуиция подсказывает нам решение. Разделим гипотенузу BC точкой D на два равных отрезка. Соединим ее с точкой A. Если отрезок AD равен по величине отрезку DC (а следовательно, и BD), то мы легко проведем требуемую окружность, поставив ножку циркуля в точку D и взяв радиусом отрезок DC. Но верно ли, что AD = DC, т. е. треугольник ADC равнобедренный? Неясно. Это выглядит правдоподобно, но во всяком случае далеко не очевидно.
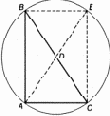
Рис. 10.2. Построение окружности, описанной вокруг прямоугольного треугольника
Теперь сделаем решающий шаг. Дополним треугольник точкой E до прямоугольника ABEC и проведем в нем вторую диагональ AE. И внезапно становится очевидной равнобедренность треугольника ADC. Действительно, из общей симметрии чертежа ясно, что диагонали равны и пересекаются в точке, которая делит их пополам, т. е. в точке D. Это еще не доказательство, но уже тот уровень ясности, когда формальное завершение доказательства не представляет труда. Например, опираясь на равенство противолежащих сторон прямоугольника (которое при желании можно вывести из еще более очевидных положений), мы завершим доказательство следующим рассуждением: треугольники ABC и AEC равны, так как сторона AC у них общая, стороны AB и ЕС равны, а углы BAC и ЕСА прямые; следовательно, угол ЕАС равен углу BCA, т. е. треугольник ADC равнобедренный, что и требовалось доказать.
Достоверность утверждений математики
Теперь о достоверности математических утверждений. Платон выводил ее из идеальности предмета математики, из того факта, что математика не опирается на призрачные и переменчивые данные чувственного опыта. Чертежи и символы, по Платону, являются лишь вспомогательным средством для математики, настоящие объекты, с которыми он оперирует, содержатся в его воображении и представляют собой результат восприятия разумом мира идей подобно тому, как чувственный опыт есть результат восприятия органами чувств материального мира. Нельзя не согласиться с тем, что воображение играет в работе математика решающую роль (как, впрочем, и во всех областях творческой деятельности). Правда, говорить, что математические объекты содержатся в воображении не совсем правильно: в основном они все-таки содержатся в чертежах и текстах, а воображение выхватывает их лишь небольшими частями. Мы не содержим, а, скорее, пропускаем математические объекты через воображение, и свойства нашего воображения определяют функционирование математического языка. Что же касается источника, определяющего содержание нашего воображения, то тут мы фундаментально расходимся с Платоном: источником является тот же чувственный опыт, что и в эмпирических науках. Поэтому математика создает — хотя и через посредство воображения — модели все того же, единственно существующего (насколько нам известно) мира, в котором мы живем.
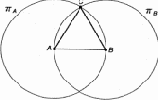
Рис. 10.3. Построение равностороннего треугольника
Надо сказать, что греческие математики, создав изумительное по красоте здание логически строгих доказательств, все же оставили в нем ряд дырок, причем дырки эти лежат, как мы уже отмечали, в самых нижних этажах здания — в области определений и элементарнейших свойств геометрических фигур. А это и свидетельствует о завуалированном обращении к столь презираемому платониками чувственному опыту. Математика времен Платона дает даже более яркий материал, чем современная математика, для опровержения тезиса о её независимости от опыта.
Первое доказываемое предложение первой книги Евклида содержит способ построения равностороннего треугольника по заданной его стороне.
Способ таков (рис. 10.3). Пусть AB — заданная сторона треугольника. Из точки A, взятой в качестве центра, опишем окружность ?A радиуса AB. Такую же окружность (?B) опишем из точки B. Обозначим через C любую из точек пересечения этих окружностей. Треугольник ABC равносторонний, ибо AC = CВ = AB.
В этом рассуждении есть логическая дырка: откуда следует, что построенные нами окружности вообще пересекутся? Вопрос этот чрезвычайно каверзный, ибо факт наличия точки пересечения C нельзя отнести ни к свойствам окружности, ни даже к свойствам пары окружностей (ибо они отнюдь не всегда пересекаются); мы имеем здесь дело с более специфическим свойством данной ситуации. Вероятно, Евклид чувствовал наличие здесь дырки, но не нашел, чем ее заткнуть.
Откуда же у нас уверенность, что окружности ?A и ?B
пересекаются? В конечном счете, разумеется, из опыта. Из опыта созерцания и рисования прямых, окружностей и линий вообще. Из безуспешных попыток провести окружности ?A и ?B таким образом, чтобы они не пересекались.
Итак, мнение Платона о полной независимости, современной ему математики от опыта нельзя признать обоснованным. Однако вопрос о природе математической достоверности требует дальнейшего исследования, ибо просто сослаться на опыт и приравнять тем самым математическую достоверность эмпирической достоверности значило бы броситься в крайность, противоположную платонизму. Ведь мы ясно ощущаем, что математическая достоверность чем-то отличается от эмпирической. Чем же?
Утверждение, что окружности радиуса AB с центрами в A и B
пересекаются (мы будем для краткости обозначать это утверждение через E1), представляется нам если не совсем, то почти абсолютно достоверным, мы просто не можем себе представить, чтобы они не пересеклись. Не можем себе представить... Этим-то и отличается математическая достоверность от эмпирической! Когда мы говорим о завтрашнем восходе солнца, мы можем представить, что солнце не взойдет. И только на основании опыта мы полагаем, что оно, вероятно, взойдет.Здесь есть две возможности, и предсказание, какая из них осуществится, имеет вероятностный характер. Когда же мы говорим, что дважды два — четыре и что окружности, построенные так, как было указано выше, пересекаются, мы не можем представить, чтобы было иначе. Мы не видим другой возможности, поэтому и утверждения эти воспринимаем как абсолютно достоверные и независимые от конкретных наблюденных нами фактов.
Духи и прочее
Теперь перейдем к «духам», которые играют такую важную роль в первобытном мышлении. Мы увидим, что появление «духов» — неизбежное следствие возникновения языка и что они исчезают (но зато с той же неизбежностью, с которой возникли) только с метасистемным переходом на уровень критического мышления.
Вдумаемся снова в ту ситуацию, когда язык уже существует, но его отношение к действительности еще не стало предметом изучения. Благодаря языку происходит нечто вроде удвоения предметов: вместо предмета Ri человек имеет дело с комплексом RiLi, где Li
— имя Ri. В этом комплексе языковый объект Li
представляет более доступную и в этом смысле более стабильную
компоненту. Произнести слово «солнце» можно независимо от того, видно ли в данный момент солнце или нет. Имя человека можно повторять сколько угодно раз, в то время как сам человек мог давно умереть. Но каждый раз его облик будет всплывать в воображении говорящего. В результате соотношение между именем и значением как бы переворачивается: объект Li приобретает признаки чего-то первичного, а объект Ri — вторичного. Нормальное отношение восстанавливается только после метасистемного перехода, когда Li наравне с Ri, а особенно связь между ними становятся объектом внимания. Пока же этого не произошло, слово Li
играет ведущую роль в комплексе RiLi, а услужливое воображение готово связать любые картины с каждым словом, употребляемым в общественной языковой практике. Одни слова языка первобытной культуры обозначают с нашей современной точки зрения реально существующие предметы, другие же обозначают с нашей точки зрения нечто реально не существующее (духи и т. п.). Но с точки зрения первобытного человека между ними нет никакой разницы, разве что чисто количественная. Обычные предметы могут быть видимы, или невидимы (когда они спрятаны или когда темно), или же видимы одними и невидимы другими. То же относится к духам, только увидеть их труднее. Их или никто не видит, или видят только колдуны. В Северной Америке у кламатов знахарь, позванный к больному, должен был совещаться с духами определенных животных.
Только тот, кто прошел пятилетний курс подготовки к знахарству, может видеть этих духов, но видит он духов так же ясно, как предметы вокруг себя. Тарагумары верили, что в реках живут большие змеи, имеющие рога и огромные глаза. Но видеть их способны только шаманы. Среди бурят было распространено мнение, что когда ребенок опасно болеет, причиной этого является маленький зверек «анокха», который поедает макушку ребенка. Анокха похож на крота или кошку, но видеть его могут только шаманы. У гуичолов есть ритуальный обряд, выполняя который они кладут головы оленьих самок рядом с головами самцов, причем считается, что у самок, как и у самцов, есть рога, хотя никто, кроме шаманов, их не видит.
Ассортимент невидимого в представлениях первобытных народов чрезвычайно широк. Здесь не только духи, представляемые как нечто бесформенное, но и предметы или существа, имеющие вполне определенный внешний вид с той лишь поправкой, что воспринимается он не всегда и не всеми. Язык в изобилии дает материал для создания воображаемых сущностей. Любое качество легко и непринужденно превращается в сущность. Отличие живого человека от мертвого дает душу, больного от здорового — болезнь. Представление о болезни как о чем-то вещественном, предметном, что может входить и выходить из тела, перемещаясь в пространстве, свойственно, пожалуй, всем первобытным народам. То же относится к душе. Любопытно, что подобно тому, как существуют различные болезни, у некоторых народов существуют и различные «души» в человеке. По наблюдениям А.Б.Эллиса, негры западно-африканского побережья различают два духа человека: «кра» и «сраман». «Кра» живет в человеке, пока он жив, отлучаясь, лишь когда человек спит: сновидения — это приключения «кра» во время сна. Когда человек умирает, его «кра» переселяется в тело другого человека или животного, а может и скитаться по свету в неприкаянном, так сказать, виде. «Сраман» же образуется лишь со смертью человека и продолжает в стране мертвых тот образ жизни, который вел покойный до смерти.
Еще ярче эта тенденция проявляется в верованиях индейцев. Манданы, например, полагают, что каждый человек носит в себе несколько духов: один из них белый, другой смуглый, третий — светлой окраски. Дакоты считают, что у человека четыре души: 1) телесная душа, которая умирает вместе с человеком; 2) дух, живущий с телом или вблизи него; 3) душа, которая ответственна за действия тела; и 4) душа, которая остается всегда возле пучка волос покойника, сохраняемого родственниками до того момента, когда его можно будет бросить на территорию врага, где он превращается в блуждающий призрак, несущий болезнь и смерть. Г.Джонс, занимавшийся исследованием верований в Корее, пишет:
Духи занимают все небо и каждую пядь земли. Они подстерегают человека на дорогах, среди деревьев, в горах, в долинах, в речках и ручьях. Они неустанно следят за ним днем и ночью... Даже в собственном доме человек не находит убежища от духов: они и здесь повсюду, они засели в штукатурке стен, повисли на балках, прилепились к перегородкам!
Духовные ценности
Прежде чем обсуждать проблему Высшего Блага и смысла жизни, надо приобрести уверенность, что обсуждать эту проблему стоит. Ибо есть много людей, стоящих на точке зрения, которую можно назвать теорией естественных ценностей, согласно которой создание этических учений — занятие пустое, если не вредное. Эта теория утверждает, что в природе человека наряду с потребностями и инстинктами, имеющими животное происхождение, заложено и стремление к специфически человеческим духовным ценностям, таким как знание, красота, справедливость, любовь к ближнему. Достижение этих ценностей доставляет высшее удовлетворение. Задача человека — развивать в себе и в других эти стремления и получать тем самым высшее удовлетворение от жизни — так сказать, максимизировать высшее удовлетворение. Это — единственная естественная цель человека, его единственное естественное назначение. Философские, религиозные и этические учения, исходящие из априорных и неизвестно откуда взятых принципов, могут только заглушить и извратить эти естественные, истинно человеческие стремления и заставить людей совершать гнусности во имя выдуманного ими Высшего Блага.
Что сказать об этой теории? Она удобна как предлог, чтобы отказаться от решения трудного вопроса. Есть у нее и то достоинство, что она оберегает от крайностей. Но, увы, она неверна. Она является в гораздо большей степени выдуманной, чем другие учения, открыто признающие свой догматический характер. Если утверждение о том, что стремление к высшим духовным ценностям заложено в природе человека, понимать в его буквальном, точном смысле, то оно приходит в противоречие с фактами. Дети, похищенные животными и выросшие вне человеческого общества, не обнаруживают понимания высших ценностей современного цивилизованного человека, они вообще не становятся полноценными людьми. Следовательно, в самой структуре развивающегося мозга нет ничего, что однозначно порождало бы те конкретные высшие устремления, о которых говорит теория естественных ценностей.
— Ах, нет! — скажет сторонник этой теории и страшно возмутится такой вульгаризации его взглядов.
Речь идет, конечно, не о конкретных формах проявления этих стремлений, а о некой их общей основе, которая для своего проявления нуждается в условиях, создаваемых обществом.
Но тогда теория естественных ценностей совершает грех подмены понятий. Сказать «общая основа» — значит ничего не сказать, если не конкретизировать сущность этой основы и ее связь с наблюдаемыми проявлениями. С точки зрения, развиваемой в настоящей книге, общая основа высших ценностей, признанных в настоящее время большей частью человечества, действительно существует, и она действительно является врожденной закодированной в структуре генов каждого человеческого существа. Это основа — способность управления ассоциированием. Условно ее можно назвать инстинктом познания (см. главу 4), но это только образное выражение. Глубокое отличие этой способности от инстинкта состоит в том, что инстинкт диктует формы поведения, а управление ассоциированием главным образом разрешает их, снимает старые запреты. Управление ассоциированием — способность чрезвычайно недифференцированная, многозначная, допускающая различные продолжения. Даже то, что мы называем мышлением, не является ее непременным следствием. А что говорить о более конкретных формах психической деятельности?
Управление ассоциированием — начало, скорее, разрушительное, чем созидательное, оно нуждается в созидательном дополнении. Таким дополнением является социальная интеграция индивидуумов — образование человеческого общества. В процессе развития общества и возникают духовные ценности. Они, конечно, далеко не случайны, но от общей основы, заложенной природой во все человеческие существа, до духовных ценностей — долгий путь, на котором руководит не логика индивидуума, а логика общества. Этот путь не однозначен и не закончен.
Теория естественных ценностей, говоря туманно об «общей основе» духовных ценностей, тем самым фактически отождествляет некоторые частные идеалы, признаваемые в настоящее время некоторыми (пусть многими) людьми, с этой самой «общей основой» — абсолютной, неизменной, заложенной в природе человека.
Из этой ошибки вытекают два следствия. Во-первых, теория естественных ценностей оказывает дурную услугу духовным ценностям, которые она выдвигает, ибо она выдвигает их на ложном основании. Она уподобляется тому доброжелателю, который стал отстаивать право крестьянского парня на человеческое достоинство не из общих принципов гуманизма, а пытаясь доказать его дворянское происхождение; обман может быть легко обнаружен, а несчастный юноша публично высечен. Во-вторых, эта теория не содержит никаких стимулов для развития духовных ценностей; она антиэволюционна, предельно консервативна.
Что мы имеем в виду, когда говорим, что те или иные ценности для человека естественны? Очевидно, что они диктуются, устанавливаются для него самой природой. Так, для животного инстинкты — это установки, которые дает ему природа, и то, что соответствует инстинктам, для него естественно. Но человеку природа не дает установок, он — высший уровень иерархии, над ним — пустое небо. Это медицинский факт, сказал бы Остап Бендер, — факт устройства человеческого мозга. Взять установки человеку неоткуда, он сам создает установки — себе и остальной природе. Для него нет ничего абсолютного, кроме отсутствия абсолютов, нет ничего естественного, кроме бесконечного развития. Все, что в данный момент представляется нам естественным, относительно и временно. И нынешние духовные ценности лишь вехи на пути человечества: не первые и не последние.
Думать о смысле жизни стоит. Думать о смысле жизни — значит создавать высшие установки и это высший вид творчества, доступный человеку. Этот вид творчества нужен всегда, ибо высшие установки должны меняться в процессе развития и всегда будут меняться. И каждый должен для себя этот вопрос как-то решить, раз уж природа предоставила ему такую возможность. Уверения, что этот вопрос надуман или неразрешим, — ложь, которую сознательно используют одни и на которую попадаются другие по умственной лени и малодушию. Он, разумеется, неразрешим на уровне чистого знания, он обязательно включает элемент свободного выбора, но одно дело — сознательный выбор, сопровождаемый изучением предмета и размышлением, и другое дело — слепое подражание навязанному кем-то образцу.Так или иначе, кто-то создает высшие установки, ибо вне общества — «в природе» — их нет. Каждый наделен этой способностью в той или иной мере; добровольно отказаться от ее использования — все равно, что здоровому животному добровольно отказаться от физического движения, от использования мышц.
Две системы
Мы имеем перед собой две кибернетические системы. Первая система — человеческий мозг. Ее функционирование — индивидуальное человеческое мышление. Ее задача — координация действий отдельных частей организма в целях сохранения его существования. Эта задача решается, в частности, путем создания моделей действительности, материальным телом которых являются нервные сети, и которые поэтому мы назовем нейронными моделями. Об устройстве мозга мы знаем, что оно основано на иерархическом принципе. Структурные элементы этой иерархии мы называем классификаторами. Функции классификаторов с учетом системного аспекта, т. е. их взаимосвязанности, — это отдельные понятия (в кибернетическом смысле слова, т. е. просто по кибернетическому определению понятия «понятие»), которые можно выделить в функционировании мозга как целого. Назовем их нейронными понятиями.
Вторая система — язык. Ее функционирование — общественная языковая деятельность. Ее задача — координация действий отдельных членов общества в целях сохранения его существования. Эта задача решается, в частности, путем создания моделей действительности, материальным телом которых являются языковые объекты и которые мы поэтому назовем языковыми моделями. Подобно мозгу язык устроен иерархически. Функциональные элементы этой иерархической системы суть логические (языковые) понятия.
Эти системы отнюдь не являются независимыми. Языковая система приводится в движение человеческим мозгом. Без мозга язык мертв. С другой стороны, и мозг находится под сильнейшим воздействием языка. Теперь проблему можно сформулировать так: какова связь между нейронными и логическими понятиями?
Обозрим источники информации об этих системах понятий. Логические понятия целиком у нас на виду; феноменологически мы знаем о них очень много, чуть ли не все, что только можно знать. О нейронных понятиях мы знаем очень мало. Нейрофизиологические исследования дают некоторую информацию только о самых нижних уровнях иерархии. О верхних уровнях никакой независимой от языка информации у нас нет.
Но мы знаем, что язык — порождение и в известном смысле продолжение мозга. Поэтому между верхними этажами нейронных понятий и нижними этажами логических понятий должна существовать тесная связь. В конце концов, взялись же откуда-то логические понятия! Логическое понятие предмета, несомненно, имеет весьма определенный нейронный коррелят, т. е. задолго до появления языка и независимо от него мир представлялся людям (и животным) в виде совокупности предметов. Из легкости, с которой люди и животные распознают некоторые отношения между предметами (в частности, трансформации во времени), можно заключить, что и для отношений между небольшим числом предметов есть специальный нейронный аппарат. Никак нельзя признать случайным, что в языках всех народов есть слова, обозначающие предметы, которые окружают человека, и простейшие отношения между ними типа отношения «внутри», которое мы использовали выше в качестве примера. Поэтому рис. 7.4 все-таки можно с известной вероятностью считать моделью устройства мозга!
Говоря о нейронных моделях и понятиях, мы имеем в виду не только врожденную основу этих понятий, но и те конкретные понятия, которые образуются на этой основе под действием потока ощущений. У высших животных и человека образование новых понятий в результате ассоциации представлений играет, как известно, огромную роль. Оно начинается с момента появления на свет и особенно интенсивно идет в молодом возрасте, образуя понятие «мясо», которое нарастает на врожденный понятийный скелет. Это обстоятельство вносит новый элемент в проблему взаимоотношения нейронных и логических понятий. Те начальные нейронные понятия, которые образуются у ребенка до того, как он начинает понимать речь и говорить, можно считать независимыми от языка и рассматривать логические понятия как их отражение. Но более сложные понятия образуются у ребенка под непосредственным и сильнейшим влиянием языка. Ассоциации представлений, лежащие в основе этих понятий, диктуются общественной языковой деятельностью, они в значительной степени навязываются ребенку взрослым в процессе обучения языку.Поэтому, анализируя взаимоотношения языковой деятельности и мышления и пытаясь оценить, сколь хорошо язык продолжает мозг, нельзя рассматривать нейронные понятия как нечто данное и сравнивать с ними логические понятия того или иного языка. Учитывая обратное влияние языковой деятельности на мышление, вопрос можно ставить только так: какие могли бы быть нейронные и логические понятия, если бы развитие языка пошло по тому или иному пути?
Феноменологическое определение семантики
Теперь нам нетрудно будет интерпретировать с точки зрения феноменологического («черноящичного») подхода основные понятия логики. Высказывание — это, очевидно, такой языковый объект, к которому относятся действия подтверждения и отрицания. Семантика языка представляется внешнему наблюдателю как функция двух аргументов — высказывания и действительного состояния вещей, принимающая одно из двух истинных значений: «верно» («да», «истина») и «неверно» («нет», «ложь»). Значение этой функции вырабатывается черным ящиком — мозгом человека, владеющего данным языком. Как это происходит, внешний наблюдатель не знает.
Высказывание — основная единица языка. Рассматривая язык как систему, мы должны поставить вопрос: как можно строить высказывание — систему из высказываний — подсистем. Так мы приходим к введению логических связок, о которых говорилось в предыдущей главе.
Реальная действительность воспринимается человеком через посредство органов чувств, она предстает перед ним как совокупность состояний рецепторов — ситуация. Если бы человек не умел управлять своими органами чувств и концентрировать внимание на каких-то частях ситуации, т. е. если бы ситуация всегда являлась для него чем-то целым и полностью заданным извне, то вся логика ограничивалась бы, вероятно, исчислением высказываний. Но на самом деле человек управляет органами чувств, например, может фиксировать зрение на том или ином предмете. Поэтому ситуация — это не просто действительность, а действительность с указателем внимания, т. е. с выделенной областью (определенной приблизительно), о которой мы говорим, что концентрируем на ней внимание.
У понятия внимание есть и психологический аспект, но мы постараемся обойтись без него. Так как, глядя на человека со стороны, можно определить, на что он смотрит (или что ощущает, нюхает и т. п.), действительность с указанием внимания можно рассматривать как аргумент функции при «.черноящичном» подходе. Чтобы уточнить положение выделенной области, люди прибегают к жестам (указывают пальцем) или к словесным пояснениям.
Результат в обоих случаях одинаков. Если вы скажете: «Я имею в виду толстую книгу, которую держит в руках девушка в розовом платье», то ваш собеседник будет переводить взгляд, пока он не примет необходимого направления.
Надо учесть и еще один аспект входных данных семантики — временной аспект. Если бы реакция мозга определялась только ситуацией в один определенный момент времени, без связи с близкими по времени ситуациями, то опять-таки логика ограничивалась бы, вероятно, одним исчислением высказываний. Однако в действительности мозг всегда хранит память о ряде прошедших ситуаций, т. е. реакция мозга — и, в частности, эталонное действие — есть всегда функция киноленты ситуаций. Мы часто не отдаем себе в этом отчета, ибо в окружающей нас среде существуют предметы, обнаруживающие относительную неизменность, и когда мы концентрируем внимание на неизменном предмете, нам кажется, что мы имеем дело не с кинолентой, а с одним кадром. На самом же деле, анализ понятия предмет, проведенный выше, показывает, что временной аспект играет в нем решающую роль. Теперь, когда мы ввели понятие указателя внимания, мы можем определить предмет как киноленту ситуаций с одной непрерывной линией указателя внимания.
До какой степени мы склонны игнорировать динамический аспект восприятия, видно из той ситуации, которую мы обычно описываем как наличие двух или нескольких выделенных предметов. Нам кажется, что мы воспринимаем каждый предмет как отдельный и вместе с тем выделяем все предметы, концентрируя на них внимание одновременно. Однако простейший психологический самоанализ убеждает, что на самом деле в такой ситуации внимание совершает быстрые перебежки с одного предмета на другой. На киноленте ситуаций линия указателя внимания будет разрывна, а именно такова, что ее можно легко дополнить до нескольких (по числу предметов) непрерывных линий (рис. 7.3).
Рис. 7.3. Разрывная линия внимания, которая может быть дополнена до двух непрерывных линий
Мы подошли вплотную к определению понятия объекта в логике.
Мы установили, что «неязыковая действительность» на рис. 7.2, которая подается на вход черного ящика, всегда частично расчленена, размечена в пространстве и времени. Ее можно представить как киноленту, на которой прочерчена линия перемещения указателя внимания. Причем оказывается, что эта-линия может быть разрывной, но допускать дополнение до нескольких непрерывных линий. Вот эти непрерывные линии и суть объекты.
Таким образом, объект логики полностью освобожден от предметного содержания, оно переносится в высказывания о данном объекте. Объект — это идентификатор, обладающий только свойством быть тождественным самому себе и обозначающий непрерывную линию внимания. Это положение было уже достаточно освещено в предыдущей главе.
Когда вместо нерасчлененной действительности мы подаем на вход черного ящика действительность, расчлененную на объекты, высказывание становится зависимым от способа расчленения, т. е. от объектов, которые мы выделяем: оно превращается в предикат.
Философия Платона
Что такое математика? О чем эта наука? Эти вопросы стали задавать греки, начав сооружать основанное на доказательствах здание математики, ибо ореол абсолютной достоверности, чуть ли не священности математического знания, который оно приобрело благодаря наличию доказательств, сразу же выделил его на фоне остальных, обыденных, житейских познаний. Ответ был дан платоновской теорией идей. Эта теория легла в основу всей греческой философии, определила стиль и образ мышления образованных греков и оказала огромное влияние на дальнейшее развитие философии и науки греко-римско-европейской культуры. Логику, которая привела Платона к его теории, установить нетрудно. О чем идет речь в математике? О точках, линиях, прямоугольных треугольниках и т. д. Но существуют ли в природе точки, не имеющие размеров. Или абсолютно прямые и бесконечно тонкие линии? Или в точности равные отрезки, углы, площади? Ясно, что нет. Выходит, что математика изучает несуществующие, воображаемые вещи, что это наука ни о чем. Но согласиться с этим было бы никак невозможно. Во-первых, математика приносила неоспоримую практическую пользу. Правда, Платон и его последователи относились к практике с презрением, но это было уже логическим следствием философии, а не ее посылкой. Во-вторых, всякий человек, изучающий математику, совершенно ясно чувствует, что имеет дело с реальностью, а не с фикцией, и никакими логическими доводами искоренить это ощущение невозможно. Следовательно, объекты математики реально существуют, но не как материальные предметы, а как образы, или идеи, потому что слово идея (??є?) по-гречески и означало образ, вид1. Идея существует вне мира материальных вещей и независимо от него. Чувственно воспринимаемые материальные вещи суть лишь несовершенные и временные копии (или тени) совершенных и вечных идей. Утверждение о реальном, объективном существовании мира идей и составляет сущность учения Платона («платонизма»).
Попытки как-то конкретизировать представления о мире идей и его взаимодействии с материальным миром вызывали в среде платоников (на протяжении многих столетий) безнадежно неразрешимые споры.
Сам Платон умудрился остаться неуязвимым, избегая конкретизации и пользуясь языком метафорическим и поэтическим. Впрочем, уже ему пришлось вступить в полемику со своим учеником Евдоксом, который не только доказывал математические теоремы, но еще и отстаивал утверждение, что идеи «примешиваются» к чувственно воспринимаемым вещам, обусловливая их свойства.
Понятия математики не являются единственными обитателями «мира идей» Платона. Всякое общее понятие претендует на место в этом мире. Рассуждение, обосновывающее эту претензию, таково. В нашем языке существуют слова и словосочетания для обозначения единичных понятий, например имена собственные: остров Самос, Афины, Гиппократ. Откуда у нас возникают эти понятия? Из чувственного восприятия соответствующих вещей. Но есть у нас и общие понятия: человек, дерево и т. п. Откуда же у нас берутся эти понятия? Ведь путем чувственного восприятия мы постигаем только конкретные понятия: данный человек, данное дерево и т. д. Если вещи порождают у нас конкретные понятия, то что же порождает общие понятия? Ответ Платона гласит: идеи; идея человека, идея дерева и т. д.
Существование мира идей обеспечивает математике прочное и высокое положение — она становится наукой об идеях. Чувственный опыт дает нам несовершенное, приблизительное знание о несовершенных, приблизительных воплощениях идей. Доказательства математики дают совершенное знание о самих идеях. «При помощи математики, — пишет Платон, — очищается и получает новую жизненную силу орган души, в то время как другие занятия уничтожают его и лишают способности видеть, тогда как он значительно более ценен, чем тысяча глаз, ибо только им одним может быть обнаружена истина».
Под влиянием идеализма Платона математики древней Греции стремились изгнать из своей науки все, что можно истолковать как обращение к данным чувственного опыта. С одной стороны, это имело положительные последствия, так как способствовало разработке техники доказательства и привело к созданию понятия о дедуктивной теории.
Греки старались сделать доказательства логически безукоризненными, исключить из них сомнительные выводы и неявные допущения, апеллирующие к наглядности. Они доказывали, а не показывали. Число явных допущений они стремились свести к минимуму, оставить из них лишь те, которые можно было считать выражением свойств «самих идей», а не вещей, т. е. свойств, открывающихся разуму, «внутреннему взору», а не органам чувств. Эти допущения включались в определения исходных понятий или, точнее, слов, ибо понятия (идеи) существовали для греков как объективная реальность, независимая от всяких слов, а определения нужны были лишь для того, чтобы не ошибиться в установлении соответствия между словами и понятиями. Так что явные допущения, делаемые греческими математиками, представлялись им не определениями в современном смысле слова (согласно которому определение порождает математический объект), а просто указаниями на те из истинных свойств реально существующих идей, которые постигаются разумом легче, чем другие, — без вспомогательных рассуждений. Если исключить это отличие и вытекающие из него вольности в обращении с элементарнейшими свойствами геометрических фигур, то в остальном греческая математика удовлетворяет самым высоким современным стандартам; в соотношении логической обоснованности понятий и строгости вывода она несравненно выше, чем европейская математика до середины XIX в. С другой стороны, образ мышления, выраженный в философии Платона, имел и отрицательное влияние. Прежде всего, он приводил к определенному «чистоплюйству» греческих ученых, нежеланию заниматься проблемами, имеющими прикладное, практическое значение. Это пренебрежение распространялось даже на приближенные вычисления. «Приближенными вычислениями стыдно заниматься свободному человеку, они — удел раба», — говорилось в то время. Действительно, приближенные вычисления не приводят к истинным соотношениям, а значит, и не имеют никакого отношения к миру идей; это занятие того же рода, как возделывание масличных деревьев или торговля оливковым маслом.Такая позиция, конечно, ограничивала приток новых задач и идей, способствовала канонизации и регламентации научной мысли, сдерживая тем самым ее развитие. Но, сверх этого, платонизм имел и более конкретное отрицательное влияние на математику, помешав грекам создать алгебраический язык. Это смогли сделать только менее вышколенные и более практичные европейцы. Ниже мы более подробно рассмотрим историю создания современного алгебраического языка и тормозящую роль платонизма, но сначала поговорим об ответах, которые дает современная наука на вопросы, поставленные в платоновское время, и о том, как выглядят ответы, данные Платоном, в исторической ретроспективе.
Физический предмет и логический объект
Опыт учит нас, что мир, в котором мы живем, характеризуется определенной устойчивостью, повторяемостью (точно так же, конечно, как непрерывной текучестью, изменяемостью). Допустим, вы видите дерево. Вы отходите от него, и изображение дерева на сетчатке вашего глаза изменяется. Но изменение это и его зависимость от ваших движений подчиняется определенному закону, который вам уже знаком по опыту наблюдения других предметов. А когда вы возвращаетесь на прежнее место, изображение становится почти в точности таким, как было раньше. Тогда вы говорите: «это — дерево», имея в виду не только ситуацию в данный момент времени (мгновенную фотографию), но и ситуации в близкие моменты. Если речь идет только о классификации отдельных ситуаций самих по себе без связи, без учета их отношения к другим ситуациям, то различия между предметами и свойствами никакого нет; понятие «мяч», как и понятие «красный», полностью исчерпывается указанием некоего множества ситуаций, и распознаватель этих понятий (естественный или искусственный) должен только уметь правильно употреблять фразы: «это — красное», «это — не красное», «это — мяч», «это — не мяч».
Положение меняется, когда надо классифицировать не отдельные ситуации, а временные последовательности ситуаций — будем их представлять в виде кинолент, кадры которых суть мгновенные ситуации. На такой киноленте «мяч» — это не просто деталь ситуации (одного кадра), а деталь ситуации, повторяющаяся на многих кадрах. Распознаватель понятия «мяч» должен не только сказать: «Да, друзья, это — мяч!» — но и выделить определенные детали на кадрах, сказав: «Вот этот мяч на кадре №137, а вот тот же самый мяч на кадре №138, вот он же на кадре №139 и вот он таким казался на кадре №120», — и т.д. Деталь ситуации, именуемая «тем самым мячом», может довольно существенно меняться вследствие изменения положения глаза относительно мяча или изменения формы самого мяча, но идентификация мяча как «того самого» остается неизменной и абсолютной.
Эта абсолютная неизменность является формой, в которой мы отражаем относительную и временную неизменность, которую находим в реальности.
Мы как бы проводим линию во времени, соединяя детали на различных кинокадрах, и объявляем, что все, что находится на этой линии, есть «тот же самый» предмет. Эта линия в сочетании с некоторым набором свойств (качеств) и образует понятие о предмете.
Логическое понятие объекта соответствует свойству физических предметов сохранять свою идентичность. Объект логики — это только идентификатор и больше ничего. Он обладает только свойством «быть тем же самым» и является именем воображаемой линии, соединяющей детали на кадрах киноленты. Если есть несколько различных классов объектов, то обычно условливаются обозначать объекты разных классов разными типами идентификаторов, например отрезки — малыми латинскими буквами, точки — большими латинскими буквами, углы — греческими буквами и т.п. Но более конкретные свойства, присущие объектам, записываются уже в виде отдельных утверждений, включающих введение обозначения. Это позволяет обходиться без конструкции со связкой «такой, что». Правда, Бурбаки в самом начале своего знаменитого трактата «Элементы математики» вводит обозначение ?x[A(x)] для некоторого объекта, обладающего свойством A(х), т. е. такого, что A{?x[A(x)]} — истинное высказывание. Однако в дальнейшем это обозначение исчезает из текста. Поэтому даже определенного названия для конструкции, сопоставляющей объект высказыванию, не установилось и в нашей таблице мы вынуждены поставить прочерк. Полное разделение труда между идентификаторами и высказываниями оказывается в конечном счете удобнее.
Возьмем для примера фразу: «Рыжий пес вдовы поручика Пшебысского загрыз бродячую кошку». При записи на языке логики эта фраза разложится на несколько высказываний, которые неявно в ней содержатся, выражаясь с помощью грамматической категории определения. Их можно объединить с помощью знака конъюнкции в одно высказывание, однако запись получится более привычной и обозримой, когда все делаемые утверждения просто выписываются, каждое с новой строчки, разделяясь запятыми вместо знаков конъюнкции.Полагая, что смысл вводимых свойств и отношений ясен из контекста, получаем следующий эквивалент указанной фразы:
«пес»(a),
«рыжий»(a),
«принадлежит»(a, b),
«вдова»(b, c),
«поручик Пшебысский»(c),
«загрыз»(a, d),
«кошка»(d),
«бродячая»(d).
Физика микромира
В физике, как и в чистой математике, по мере возрастания абстрактности теорий укоренялось понимание их языкового характера. Решающий толчок этот процесс получил после того, как в начале XX в. физика вторглась в пределы мира атомов и элементарных частиц и были созданы теория относительности и квантовая механика. Особенно большую роль сыграла квантовая механика. Эту теорию вообще невозможно понять, если не напоминать себе постоянно, что она представляет собой лишь языковую модель микромира, а не изображение того, как он выглядел бы «на самом деле», если бы можно было бы увидеть в микроскоп с чудовищным увеличением, и что такого изображения нет и быть не может. Поэтому представление о теории как о языковой модели действительности стало составной частью современной физики, стало необходимым физикам для успешной работы. В результате среди физиков стало меняться и внутреннее отношение к характеру своей деятельности. Если раньше физик-теоретик ощущал себя открывателем чего-то существовавшего до него и независимо от него, подобно мореплавателю, открывающему новые земли, то сейчас он ощущает себя, скорее, создателем чего-то нового, подобно мастеру, искусно владеющему своей профессией и создающему новые здания, машины, инструменты. Это изменение проявилось даже в оборотах речи. О Ньютоне говорят по традиции, что он «открыл» исчисление бесконечно малых и небесную механику; о современном ученом скажут, что он «создал», или «предложил», или «разработал» новую теорию; выражение «открыл» прозвучит архаично. Это, конечно, нисколько не ущемляет достоинства теоретиков, ибо созидание – занятие не менее почетное и вдохновляющее, чем открытие.
Почему же квантовая механика потребовала осознания «языковости» теорий?
Согласно первоначальной атомистической концепции атомы представлялись просто очень маленькими частицами вещества, маленькими тельцами, имеющими, в частности, определенную форму и цвет, от которых зависят физические свойства и цвет больших скоплений атомов. Атомная физика начала XX в.
перенесла понятие атома («неделимый») на элементарные частицы — электроны и протоны (к которым вскоре добавился нейтрон), а слово «атом» стало обозначать конструкцию, состоящую из атомного ядра (оно, по первоначальной гипотезе, являлось скоплением протонов и электронов), вокруг которого вращаются электроны, как планеты вокруг Солнца. Такое представление о строении вещества считалось гипотетическим, но чрезвычайно правдоподобным. Сама гипотетичность понималась в том смысле, о котором мы говорили выше: планетарная модель атома должна быть либо истинной, либо ложной. Если она истинна (а в этом почти не было сомнений), то электроны — это «на самом деле» маленькие частички вещества, которые описывают определенные траектории вокруг ядра. Правда, по сравнению с атомами древних элементарные частицы уже стали утрачивать некоторые, казалось бы, совершенно необходимые для частиц вещества свойства. Стало ясно, что понятие цвета совершенно неприменимо к электронам и протонам; не то, чтобы мы не знали, какого они цвета, а просто вопрос этот не имеет смысла, ибо цвет есть результат взаимодействия со светом по крайней мере атома в целом, а точнее — скопления многих атомов. Возникали также сомнения относительно понятий о форме и размерах электронов. Но святая святых представления о материальной частице — наличие у частицы в каждый момент времени определенного положения в пространстве — оставалось несомненным и само собой разумеющимся.
Формализация и метасистемный переход
Превращение языка в независимую от создавшего его человеческого мозга реальность, происходящее благодаря формализации, имеет далеко идущие последствия. Только что созданная языковая машина (теория) становится, как часть окружающего человека мира, объектом изучения и описания с помощью нового языка. Происходит, таким образом, метасистемный переход. Новый язык называют по отношению к описываемому языку метаязыком, а теории, сформулированные на этом языке и касающиеся теорий на языке-объекте, — метатеориями. Если метаязык формализованный, то он в свою очередь может стать объектом изучения с помощью языка следующего уровня и этот метасистемный переход может повторяться неограниченно.
Таким образом, формализация языка порождает эффект лестницы (см. главу 5). Подобно тому, как овладение общим принципом производства орудий для воздействия на предметы приводит к многократному повторению метасистемного перехода и созданию иерархической системы промышленного производства, так и овладение общим принципом описания (моделирования) действительности с помощью формализованного языка приводит к созданию иерархической системы формализованных языков, на которой основаны современные точные науки. Обе иерархии имеют значительную высоту. Невозможно построить реактивный самолет голыми руками. То же относится и к инструментам, необходимым для постройки самолета. Надо начинать с простейших орудий и пройти всю иерархию сложности инструментов, чтобы добраться до самолета. Точно так же, чтобы обучить дикаря квантовой механике, придется начать с арифметики.
Формализация научного языка
Можно ли сделать отсюда вывод, что в науке наступил информационный кризис? Пожалуй, еще нет. О кризисе говорить рано, но уже видно, что вследствие непрерывного возрастания потока информации кризис наступит в недалеком будущем, если не произойдет каких-либо качественных перемен в организации научных исследований. До сих пор организация научных исследований имеет формы, сложившиеся традиционно, сами по себе. Они не только не являются результатом научного исследования, но до самого недавнего времени не были даже его предметом. Итак, необходим научный подход к проблеме организации научной деятельности, т. е. новый метасистемный переход: научное управление системой науки. Этот метасистемный переход имеет два аспекта. Первый аспект не выходит за рамки науки как подсистемы в системе культуры и создает новый уровень иерархии в рамках науки как языковой, по преимуществу, деятельности. Это то, что мы в предыдущей главе назвали метанаукой. Второй аспект касается науки как социального явления. Этот аспект получил название науки о науке или науковедения.
Понятие метанауки мы ввели в предыдущей главе, отправляясь от проблем, стоящих перед теоретической физикой, и без всякой связи с информационной проблемой. Впрочем, уже говоря о математике, мы заметили, что метанаучный концептологический подход является организующим началом для того безграничного числа теорий и задач, которые может породить аксиоматическая знаковая математика. Связь с информационной проблемой в естественных и технических науках здесь очевидна. Можно много чего исследовать, и можно смелой рукой начертать множество планов исследований. Но, во-первых, надо иметь ясные принципы планирования — планы планов. Иначе возникает анархия планов, животная борьба за существование между планами, и в этой борьбе, увы, зачастую решающими оказываются факторы, далекие от интересов науки: престижные соображения, личные связи и т. п. Во-вторых, необходимо, чтобы язык естественных наук и техники был полностью формализован, тогда совокупность человеческих знаний предстанет в виде стройной системы и тогда только, кстати говоря, и станет возможным выбирать научные принципы планирования науки.
Не надо думать, что процесс формализации есть нечто «формальное», т. е. синтаксическое, сводящееся лишь к новым обозначениям. Задача формализации научного языка — это концептологическая, семантическая задача, задача выработки новых понятий, подобная формализации и аксиоматизации, происшедшей в математике.
Полностью формализованный язык — это язык, доступный машине. Имея формализованный каркас в научном здании, мы можем отделить работы, которые могут быть выполнены машинами, автоматами, от работ, которые требуют творческого участия человека, и выполнять машинные работы с помощью машин. Конечно, и сейчас уже простейшие из таких задач решаются машинами (автоматика, использование ЭВМ). Но формализация позволит существенно, многократно повысить уровень задач, решаемых машинным образом. Прежде всего, это относится к обработке потоков информации. Систематизация и хранение информации, отбор нужной информации, простейшие преобразования информации — эти и другие задачи, образующие сейчас информационную проблему, не могут удовлетворительно решаться на машинах без полной формализации языка. Именно трудности формализации языка ограничивают в настоящее время применение вычислительных машин в информатике. Успехи, которые здесь достигаются, связаны в основном с более или менее успешной формализацией более или менее обширной части научно-технического языка.
Формализация теории множеств
Понятие совокупности, или множества, принадлежит к числу фундаментальнейших понятий, данных нам природой, и предшествует понятию числа. В своем первичном виде оно не дифференцируется на понятие конечного и бесконечного множеств, однако, эта дифференциация появляется весьма рано; во всяком случае, в древнейших письменных памятниках мы уже находим понятие о бесконечности и бесконечном множестве. Это понятие использовалось в математике испокон веков, оставаясь чисто интуитивным и само собой разумеющимся, и не подвергаясь специальному рассмотрению, пока Георг Кантор (1845-1918) не создал в 70-х годах свою теорию множеств, которая вскоре легла в основу всей математики. Понятие множества (конечного и бесконечного) остается у Кантора по-прежнему интуитивным, он определяет его следующим образом: «Под множеством понимают объединение в одно целое объектов, хорошо различимых нашей интуицией и нашей мыслью». Это «определение» является, конечно, не в большей степени математическим определением, чем «определение» Евклида «точка есть то, что не имеет частей». Но, несмотря на столь нечеткие исходные позиции, Кантор (опять-таки подобно греческим геометрам) создал стройную и логически последовательную теорию, с помощью которой ему удалось привести в замечательный порядок основные понятия и доказательства математического анализа. («Просто поразительно, — пишет Н.Бурбаки, — какую четкость постепенно приобретают у него понятия, которые, казалось, были безнадежно запутаны в классической концепции континуума».) С теорией множеств математики получили единообразный метод создания новых понятий — конструктов и доказательства их свойств. Так, например, действительное число есть множество всех последовательностей рациональных чисел, имеющих предел; отрезок действительной прямой — множество действительных чисел; функция — множество пар (x, f), где х и f — действительные числа.
К концу XIX в. теория множеств Кантора получает признание и естественным образом сочетается с аксиоматическим методом.
Но тут разражается знаменитый «кризис основ» математики, продолжавшийся в течение трех десятилетий. В теории множеств были обнаружены «парадоксы», т. е. построения, приводящие к противоречиям. Первый парадокс обнаружил Бурали-Форти в 1897 г., затем появилось еще несколько. Мы приведем в качестве примера парадокс Рассела (1905 г.), который можно изложить, опираясь лишь на первичные понятия теории множеств и не нарушая в то же время требований математической строгости. Парадокс этот таков. Определим M как множество всех тех множеств, которые не содержат себя в качестве элемента. Казалось бы, это определение вполне законно, ибо образование множеств из множеств — одна из основ теории Кантора. Между тем оно приводит к противоречию. Чтобы сделать его более ясным, обозначим через Р(х) свойство множества х быть элементом самого себя. В символической форме
P(x) ? x
? x. (12.1)
Тогда по определению множества М все его элементы х обладают свойством, противоположным Р(х):
x ? M ? ¬P(x). (12.2)
Теперь поставим вопрос: является ли само множество M своим элементом, т. е. истинно ли P(M)? Если P(M) истинно, то M
? M, согласно определению (12.1). Но в таком случае, подставляя M
вместо х в утверждение (12.2), мы получаем ¬P(M). Если M
входит в множество M, то по определению последнего оно не должно обладать свойством P. И напротив, если P(M) ложно, т. е. имеет место P(M), то согласно (12.2) М должно входить в M, т. е. Р(М) истинно. Таким образом, P(M) не может быть ни истинным, ни ложным. С точки зрения формальной логики мы доказали две импликации:
P(M) ? ¬P(M), ¬P(M) ? P(M).
Если выразить импликацию через отрицание и дизъюнкцию и воспользоваться свойством дизъюнкции A ? A ? A, то первое высказывание превратится в ¬P(M), а второе — в P(M). Мы получили формальное противоречие и, следовательно, из теории множеств можно вывести что угодно.
Парадоксы создали угрозу для теории множеств и основанного на ней математического анализа; возникло несколько философско-математических направлений, предлагавших различные выходы из тупика.
Наиболее радикальное направление во главе с Брауэром, получившее название интуиционизма, потребовало не только полного отказа от теории множеств Кантора, но и коренного пересмотра логики. Интуиционистская математика оказалась довольно сложной и с трудом поддающейся развитию, а поскольку классический анализ при этом выбрасывался на свалку, такая позиция была найдена неприемлемой для большинства математиков. «Никто не может изгнать нас из рая, созданного для нас Кантором», — заявил Гильберт, и он нашел выход, который сохранил основное содержание теории множеств и в то же время устранил парадоксы и противоречия. Вместе со своими последователями Гильберт сформировал главное русло, по которому направилось течение математической мысли.
Решение Гильберта полностью соответствует духу развития европейской математики. Если Кантор рассматривал свою теорию с сугубо платоновских позиций — как исследование свойств реально существующих и действительно («актуально») бесконечных множеств, то, по Гильберту, множества надо рассматривать просто как некоторые объекты, удовлетворяющие аксиомам, аксиомы же надо сформулировать так, чтобы определения, приводящие к парадоксам, стали невозможны. Первая система аксиом теории множеств, не порождающая противоречий, была предложена Цермело в 1908 г., затем она была модифицирована. Были предложены и другие системы, однако отношение к теории множеств осталось неизменным. В современной математике теория множеств играет роль каркаса, скелета, который соединяет в единое целое все ее части, но не виден снаружи и не соприкасается непосредственно с внешним миром.
По-настоящему понять эту ситуацию и совместить формальный и содержательный аспекты математики можно только с «языковой» точки зрения на математику. Эта точка зрения, которую мы настойчиво проводили на протяжении всей книги, приводит к следующей концепции. Никаких актуально бесконечных множеств нет ни в реальности, ни в нашем воображении. Единственное, что мы можем найти в своем воображении, это представление о потенциальной бесконечности, т.
е. о возможности неограниченно повторять какой- либо акт. Здесь надо полностью согласиться с интуиционистской критикой канторовской теории множеств и отдать должное ее глубине и проницательности. Однако для того, чтобы использовать теорию множеств так, как это делает современная математика, вовсе не надо насиловать свое воображение и пытаться представить «актуальную» бесконечность. «Множества», которые используются в математике — это просто символы, языковые объекты, используемые для построения моделей действительности. Постулируемые свойства этих объектов частично соответствуют интуитивным понятиям совокупности и потенциальной бесконечности, поэтому интуиция частично помогает в развитии теории множеств, но иногда и обманывает. Когда новый математический (языковый) объект определяется как «множество», построенное так-то и так-то, это определение не имеет никакого значения для связи объекта с внешним миром, т. е. для его интерпретации, а нужно лишь для привязки к каркасу математики, для зацепления внутренних колесиков математических моделей.
Таким образом, язык теории множеств является фактически метаязыком по отношению к языку содержательной математики и в этом он подобен языку логики. Если логика — это теория доказательства математических утверждений, то теория множеств — это теория конструирования математических языковых объектов.
Почему же именно интуитивное понятие множества легло в основу математического конструирования?
Определить вновь вводимый математический объект — значит указать его семантические связи с уже введенными объектами. За исключением тривиального случая, когда речь идет о пере обозначении — замене знака на знак, этих связей всегда бывает много и в них может участвовать много ранее введенных объектов. И вот вместо того, чтобы говорить, что новый объект связан так-то и так-то с такими-то и такими-то старыми объектами, говорят, что новый объект есть множество, построенное так-то и так-то из старых объектов. Например, рациональное число есть результат деления двух натуральных чисел: числителя на знаменатель.
Число 5/7 есть объект х такой, что значение функции «числитель» (x) есть 5, а значение функции «знаменатель» (x) есть 7. Между тем в математике определяют рациональное число просто как пару натуральных чисел. Точно так же надо было бы говорить только о реализации
действительного числа различными последовательностями рациональных чисел, понимая под этим определенную семантическую связь между новыми и старыми языковыми объектами. Вместо этого говорят, что действительное число есть множество последовательностей рациональных чисел. В настоящее время эту терминологию следует рассматривать как пережиток платоновских воззрений, согласно которым важны не языковые элементы, а скрывающиеся за ними элементы «идеальной реальности»; поэтому, чтобы приобрести право на существование, объект должен был определяться как «реальное» множество. Идея множества выдвинулась на «руководящую работу» в математике как один из аспектов связи имя-значение (а именно того факта, что значением обычно является конструкция, состоящая из некоторого числа элементов), а вряд ли стоит доказывать, что связь имя-значение всегда была и будет основой языкового конструирования.
Формализованный язык
«Следующая остановка — станция Апрелевка, — доносится хриплый голос из репродуктора. — Повторяю: станция Апрелевка. На станции Победа поезд остановки не имеет».
Вы едете на электричке по Киевской железной дороге, а поскольку вы забыли захватить книгу и делать вам нечего, вы начинаете размышлять о том, как небрежно мы все еще относимся к нашему родному языку. В самом деле, что за нелепое выражение «остановки не имеет»? Не проще ли сказать «не останавливается». Ах, эти канцелярские, казенные выражения. Уж пишут об этом, пишут, а толку все нет.
Однако, если вы не сходите в Апрелевке и у вас есть время на дальнейшие размышления, вы поймете, что дело здесь вовсе не в небрежном отношении к родному языку, а в том, что «остановки не имеет» означает не совсем то же самое, что «не останавливается». Понятие остановки в железнодорожном лексиконе не тождественно с понятием прекращения движения. Ему можно дать следующее определение, не слишком изящное, но достаточно точное: остановка — это преднамеренное прекращение движение поезда, сопровождаемое принятием мер, необходимых для обеспечения выхода пассажиров из вагонов и входа в вагоны. Это очень важное для железнодорожников понятие, и оно связано именно с существительным «остановка», а не с глаголом «останавливаться». Так что если, например, машинист остановил поезд, но не открыл пневматических дверей, то поезд «остановился», но не «возымел остановку».
Железнодорожник, делавший объявление, конечно, не производил такого лингвистического анализа. Он просто воспользовался привычным профессиональным термином, что позволило ему выразить свою мысль совершенно точно, хотя и несколько коряво с точки зрения непрофессионала. Это — проявление весьма распространенного явления: когда язык употребляется в сравнительно узких профессиональных целях, наблюдается тенденция к ограничению числа используемых терминов и приданию им более четкого и постоянного смысла. Происходит, как говорят, формализация языка. Если этот процесс довести до логического завершения, то язык будет полностью формализованным.
Понятие о формализованном языке можно определить следующим образом.
Обратимся к нашей схеме использования языковых моделей действительности (см. рис. 9.5) и поставим вопрос: каким образом выполняется преобразование L1 > L2, от какой информации оно зависит? Можно представить себе две возможности.
Преобразование L1 > L2 определяется исключительно языковыми объектами Li, которые в нем участвуют, и не зависят от тех языковых представлений Si, которые им соответствуют по семантике языка. Иначе говоря, языковая деятельность зависит только от «формы» языковых объектов, но не от их «содержания» (значения). Результат преобразования языкового объекта Li зависит не только (и не столько) от вида самого объекта Li, но и от представления Si, которое он порождает в голове человека, от ассоциаций, в которые он входит, а, следовательно, от личного жизненного опыта человека. В первом случае мы называем язык формализованным, во втором неформализованным.
Подчеркнем, что полная формализация языка не обязательно означает его полную алгоритмизацию, т. е. такое положение, когда вся языковая деятельность сводится к выполнению четких и однозначных предписаний, в результате которых каждый языковый объект L1 преобразуется в совершенно определенный объект L2. Правила преобразования L1 > L2 могут формулироваться в виде более или менее жестких ограничений и оставлять определенную свободу действий, важно только, чтобы эти ограничения зависели лишь от вида объекта L1 и потенциальных объектов L2 самих по себе и не зависели от семантики языковых объектов.
Данное нами определение формализованного языка относится к случаю, когда язык используется для создания моделей действительности. Когда язык служит средством передачи управляющей информации (язык приказов), имеет место совершенно аналогичное деление на два возможных типа реакции.
Человек реагирует на приказ строго формально, т. е. его действия зависят только от той информации, которая содержится в тексте приказа, рассматриваемом как изолированная материальная система. Действие человека зависит от тех представлений и ассоциаций, которые вызывает у него приказ.
Таким образом, он использует фактически гораздо большую информацию, чем та, которая содержится в тексте приказа. Принципиальной разницы между языком приказов и языком моделей нет. Приказ «прячься!» можно трактовать как модель «если ты не спрячешься, то рискуешь потерять жизнь». Различие между приказом и моделью — в деталях использования информации. В обоих случаях формализованность языка приводит к определенному отделению синтаксиса от семантики, к отрыву материальных языковых объектов от связанных с ними представлений, к приобретению языковыми объектами качеств независимой системы.
В зависимости от того, какого типа язык используется, можно говорить о неформальном и формальном мышлении.
При неформальном мышлении языковые объекты важны главным образом постольку, поскольку они вызывают у нас определенные комплексы представлений. Слова здесь — веревочки, дергая за которые мы извлекаем из памяти частицы нашего жизненного опыта, переживаем их вновь, сопоставляем, сортируем и т. п. Результатом этой внутренней работы является преобразование представлений S1 > S2, которое моделирует перемены в окружающей среде R1 > R2. Это не значит, однако, что неформальное мышление тождественно с безъязыковым. Во-первых, уже само расчленение потока ощущений зависит от системы понятий, фиксированной в языке. Во-вторых, и в процессе преобразования S1 > S2 «натуральный вид» языкового объекта — слово — играет немаловажную роль: мы очень часто пользуемся ассоциацией именно между словами, а не представлениями. Поэтому формулу неформального мышления можно изобразить в виде
(S1, L1) > (S2, L2).
При формальном мышлении мы оперируем с языковыми объектами как с некоторыми самостоятельными и самодовлеющими сущностями, забывая на время об их семантике и вспоминая о ней лишь тогда, когда надо интерпретировать полученный результат или уточнить исходные посылки. Формула формального мышления такова:
S1 > L1 > L2 > S2.
Для того чтобы формальное мышление приводило к правильным результатам, семантика языка должна обладать определенными свойствами, которые мы характеризуем такими терминами, как точность, определенность, однозначность.
Если семантика этими свойствами не обладает, то мы не сможем ввести такие формальные преобразования L1 > L2, чтобы, пользуясь ими, получать всегда правильный результат. Можно, конечно, кок-то установить формальные правила преобразований и получить, таким образом, формализованный язык, но это будет язык, приводящий иногда к ложным выводам. Вот пример умозаключения, приводящего к ложному результату из-за неоднозначности в семантике:
|
Ваня — цыган. |
|
Цыгане пришли в Европу из Индии. |
|
Следовательно, Ваня пришел в Европу из Индии. |
Формула
Место древнего Египта и Вавилона в истории математики можно определить следующим образом: в этих культурах впервые появилась формула. Под формулой мы понимаем не только буквенно-цифровое выражение современного алгебраического языка, но вообще всякий языковый объект, являющийся точным (формальным) предписанием, как производить преобразование L1 > L2 или какие-либо вспомогательные преобразования в рамках языка. Формулы представляют собой важнейшую часть любой развитой теории, хотя, конечно, не исчерпывают ее, ибо в теорию входит еще семантика языковых объектов Li. Утверждение о связи между величинами сторон в прямоугольном треугольнике, содержащееся в теореме Пифагора, — это формула, если даже оно выражено словами, а не буквами. Типовая задача с описанием хода решения («делай так!») и с примечанием, что числа могут быть произвольны (это может быть не высказано, но подразумеваться), — это тоже формула. Именно такие формулы и дошли до нас в египетских папирусах и на вавилонских глиняных табличках.
1 См. замечания И.Н. Веселовского к переводу книги: Ван дёр Варден Б. Пробуждающаяся наука. М.: Физматгиэ, 1959.
2 C небольшими сокращениями.
3 Этот отрывок дошел до нас через Прокла (V в.н.э) — комментатора Евклида.
Функции
В приведенном выше примере один из предикатов, а именно предикат «поручик Пшебысский»(c), отличается от остальных предикатов своей явной неэлементарностью. В свойстве «быть поручиком Пшебысским» мы различаем две стороны: иметь чин и иметь фамилию Пшебысский. Поэтому и предикат выражается двумя словами. Конечно, мы могли бы представить каждое из этих слов в виде отдельного предиката, но тот факт, что «поручик» это чин объекта c, а «Пшебысский» — его фамилия, при этом не нашел бы отражения, почему мы и сочли такое разделение бессмысленным.
«Фамилия» и «чин» — это примеры функции от одного аргумента, т. е. конструкции, сопоставляющей объекту-аргументу объект-значение функции. Функция записывается так, как это принято в математике: «фамилия»(x), «чин»(x) и т. п. Если аргументов несколько, то они отделяются друг от друга запятой и мы имеем дело с функцией нескольких переменных. Эта конструкция сопоставляет набору объектов-аргументов (порядок их важен) объект-значение. Пример функции двух аргументов: «результат игры в шахматы» (x, у). Приведем примеры функций из математики. Функции одного аргумента: sin(x), |x|. Функции двух аргументов: арифметические действия, которые можно записывать так: +(х, у), -(х, у) и т.д.; расстояние r(A, B) между двумя точками A и B в пространстве. Функции трех аргументов: угол, образуемый в точке B направлениями на точку A и C; обозначение ?(A, B, C), сокращенно ?ABC.
Не всякий объект можно подставить в качестве аргумента (аргументов) в заданную функцию. Если объект a — рыжий пес, то, очевидно, конструкция «чин»(a) бессмысленна. Бессмысленна и конструкция +(a, B), где a — число, а, B — точка в пространстве. Множество объектов, которые могут быть аргументами функции (для функций от многих аргументов — множество наборов объектов), называется ее областью определения. Область определения функции «чин» (x) образуют все те объекты, которые являются военнослужащими. Объекты, которые могут быть значениями данной функции, образуют множество, которое называют областью значений функции.
В область значений функции «чин»(x) входят такие объекты, как «прапорщик», «поручик», «майор» и др., но никак не «3.14» или «рыжий пес». Функция «чин»(x) приписывает каждому военнослужащему определенный чин.
Когда мы имеем дело с функциями, одно из отношений между объектами становится особенно важным, а именно отношение равенства. Оно необходимо для установления соответствия между функциональными конструкциями и наименованиями объектов из области значений функций. Выделяя равенство из массы других отношений, мы сохраним для него привычную запись х = у вместо записи в виде предиката =(х, у). Тот факт, что объект c
имеет фамилию «Пшебысский» и чин «поручик», будет выглядеть следующим образом:
(«фамилия»(c) = «Пшебысский») ? («чин»(c) = «поручик»).
Отношение равенства можно определить формально с помощью следующих четырех утверждений:
(?a)(a = a).
(?a)(?b)[(a = b) ? (b = a)].
(?a)(?b)(?c)[(a
= b) ? (b = c) ? (a = c)].
(?a)(?b)[(a = b) ? (W(a) ? W(b))].
Последнее утверждение верно для любого высказывания W(x), зависящего от переменной х. В качестве упражнений предлагаем читателю перевести эти утверждения на естественный язык.
В одном из примеров, приведенных выше, мы видели предикат D(x, y), имеющий смысл: «x является делителем у». Понятие делимости целиком определяется операцией (функцией) умножения, поэтому предикат D(x, у) может быть выражен через функцию. Натуральное (т. е. целое положительное) число p является делителем числа n тогда и только тогда, когда существует такое натуральное число т, что n
= p × m. На языке исчисления предикатов
(?p)(?n)[D(p, n) ? (?m)(n = ×(p, m))].
Каждой функции от n аргументов можно поставить в соответствие n+1-местный предикат, выражающий то отношение, что один (скажем, последний) аргумент есть данная функция от остальных аргументов. Например, функции ×(x, y) соответствует предикат M(x, y, z), который дает верное высказывание в том и только в том случае, когда z = ×(x, y).В общем случае функции f(x, у, ..., z) соответствует предикат F(x, у, ..., z, u), обладающий свойством
(?x)( ?y)...(?z)( ?u)[F(x, у, ..., z, и) ? (f(x, у, ..., z) = u)].
Предикат F выражает фактически то же понятие, что и функция f. Любое высказывание, содержащее функциональные символы, можно переписать, используя лишь предикатные символы и введя дополнительно некоторое число объектных переменных. Таким образом, обе конструкции, порождающие новые объекты, — конструкция со связкой «такой, что» и функция — не являются принципиально необходимыми и без них можно обойтись. Однако в отличие от конструкции «такой, что» функциональные символы весьма удобны и широко используются в логике.
Геометрическая алгебра
На рис. 11.1 показана хорошо известная геометрическая трактовка соотношения
(a + b)2 = a2 + 2ab + b2.
Столь же тривиальное с алгебраической точки зрения равенство
(a + b)(a - b) = a2 - b2
требует уже более сложного геометрического рассмотрения. Ему соответствует следующая теорема во второй книге «Начал» Евклида (рис. 11.2):
«Если прямая линия разделена на равные и неравные части, то прямоугольник, содержащийся между неравными частями1 всей прямой, вместе с квадратом отрезка между точками деления равен квадрату на половине прямой».
Доказывается теорема следующим образом.
Прямоугольник ABFE равен прямоугольнику BDHF. Прямоугольник BCGF равен прямоугольнику GHKJ. Если к этим двум прямоугольникам (образующим вместе прямоугольник ACGE, «содержащийся между неравными частями всей прямой») добавить квадрат FGJI, то получится как раз квадрат BDKI, построенный «на половине прямой». Итак, мы имеем равенство
(a + b)(a - b) + b2 = a2,
эквивалентное приведенному выше, но не содержащее трудно интерпретируемого вычитания площадей.
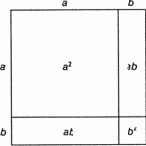
Рис. 11.1. Геометрическая трактовка тождества (a + b)2 = a2 + 2ab + b2
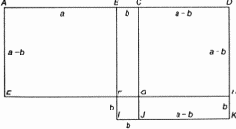
Рис. 11.2. Геометрическая трактовка тождества (a + b)(a - b) = a2 - b2
Ясно, что если даже эти простейшие алгебраические соотношения требуют в геометрической трактовке определенных усилий для понимания формулировки теоремы и изобретательности для ее доказательства, то далеко по этому пути продвинуться невозможно. Во всем, что касается собственно геометрии, греки проявили себя как искуснейшие мастера. Но та линия развития математики, которая началась с алгебры, а затем породила анализ бесконечно малых и современные аксиоматические теории, т. е. линия, связанная с использованием не языка фигур, а языка символов, оказалась им совершенно недоступной. Греческая математика осталась ограниченной, сдавленной узкими рамками понятий, имеющих наглядный геометрический смысл.
Химическая эра
Историю жизни до появления человека можно разбить на два периода, которые мы назовем «химической» эрой и «кибернетической» эрой. Границей между ними служит появление животных с четко оформленной нервной системой, включающей органы чувств, нервные волокна для передачи информации и нервные узлы для ее преобразования. Такая терминология не означает, конечно, что понятия и методы кибернетики неприменимы к жизни «химической» эры; просто животное «кибернетической» эры является классическим объектом кибернетики, на котором она возникла и оформилась как научная дисциплина.
Историю и логику эволюции в докибернетическом периоде мы рассмотрим лишь бегло, ссылаясь на воззрения современных биологов1. В этом периоде можно выделить три этапа.
На первом этапе закладываются химические основы жизни, образуются макромолекулы нуклеиновых кислот и белков, обладающие свойством редупликации — снятия копий, «отпечатков», когда одна макромолекула служит матрицей для синтеза из элементарных радикалов подобной ей макромолекулы. Основной закон эволюции, который вступает в действие на этом этапе, приводит к тому, что матрицы, обладающие большей интенсивностью воспроизведения, получают преимущество перед матрицами с меньшей интенсивностью воспроизведения, в результате чего образуются все более сложные и активные макромолекулы и системы макромолекул. Биосинтез требует свободной энергии. Первичным ее источником является солнечное излучение. Продукты частичного распада живых образований, непосредственно использующих солнечную энергию (фотосинтез), также содержат некоторый запас свободной энергии, который может быть реализован с помощью уже имеющейся химии макромолекулы. Он и реализуется специальными образованиями, для которых продукты распада служат вторичным источником свободной энергии. Так возникает расслоение жизни на растительный и животный миры.
Второй этап эволюции — возникновение и развитие у животных двигательного аппарата.
В характеристике доступа к источнику энергии есть существенное различие между растениями и животными.
При данной освещенности интенсивность поглощения солнечной энергии зависит только от величины поверхности растения, но никак не от того, движется оно или покоится. Совершенствование растений пошло по пути создания выносных светоуловителей — зеленых листьев, крепящихся на системе опор и стрел — стеблей, веток и т. п. Конструкция эта отлично работает, обеспечивая медленное перемещение зеленых поверхностей к свету, отвечающее медленному изменению освещенности.
Совсем другое положение у животного, в частности, у самого примитивного животного, например, амебы. Источник энергии — пища — заполняет среду вокруг него. Приток энергии определяется скоростью диффузии пищевых молекул через оболочку, отделяющую пищеварительный аппарат от внешней среды. Скорость диффузии зависит не только — и даже не столько — от величины поверхности пищеварительного аппарата, сколько от движения этой поверхности относительно среды, дающего возможность выедать пищу из различных ее участков. Поэтому даже простое хаотическое движение в среде или, напротив, движение среды относительно организма (так делают, например, губки, прогоняя через себя воду с помощью ресничек) имеет большое значение для примитивного животного и, следовательно, появляется в процессе эволюции. Возникают специальные образования (внутриклеточные — у одноклеточных организмов и содержащие группы клеток — у многоклеточных), основной функцией которых является производство движения.
На третьем этапе эволюции движения животных становятся направленными, и у них появляются зачатки органов чувств и нервной системы. Это также является естественным следствием основного закона. Животному выгоднее двигаться в том направлении, где концентрация пищи выше, а чтобы осуществить это движение, надо иметь датчики, характеризующие состояние внешней среды в различных направлениях (органы чувств), и информационные каналы связи между этими датчиками и двигательным аппаратом (нервная система). Вначале нервная система чрезвычайно примитивна. Органы чувств различают лишь несколько ситуаций, на которые животное должно реагировать по-разному.Объем информации, который передает нервная система, ничтожен. Специальный аппарат для обработки информации отсутствует. С течением времени органы чувств усложняются и поставляют все больше информации о внешнем мире. Одновременно совершенствуется двигательный аппарат. Это предъявляет все увеличивающиеся требования к пропускной способности нервной системы. Появляются специальные образования — нервные узлы, которые перерабатывают информацию, поступающую от органов чувств, в информацию, управляющую органами движения. Начинается новая — «кибернетическая» эра.
Иерархия целей и планов
В схеме регулирования на рис. 2.6 цель изображена как нечто единое, целое. Однако мы хорошо знаем, что бывают сложные цели, в процессе достижения которых система ставит пред собой промежуточные, «частичные», цели. Мы уже приводили примеры двухфазных движений: чтобы вспрыгнуть на стул, кошка сначала приседает, а потом подпрыгивает. В более сложных ситуациях цели образуют иерархию, состоящую из многих уровней. Предположим, вы ставите перед собой цель приехать из дома на работу. Это ваша «высшая» цель в данный момент. Припишем ей индекс (номер уровня) нуль. Чтобы приехать на работу, вам нужно выйти из дома, пройти к остановке автобуса, доехать до нужной остановки и т. д. Это цели с индексом минус единица. Чтобы выйти из дома, надо выйти из квартиры, спуститься в лифте и выйти из подъезда. Это цели с индексом минус два. Чтобы спуститься в лифте, надо открыть дверь, войти в лифт и т. д. — индекс минус три. Чтобы открыть дверь лифта, надо протянуть руку к дверной ручке, нажать на нее и потянуть к себе — индекс минус четыре. Эти цели можно уже, пожалуй, считать элементарными.
Цель вместе с указанием способа ее достижения, т. е. разложения на подчиненные цели, называют планом действия. Наш пример есть фактически описание плана приезда на работу. В цели самой по себе, которая в данном случае есть представление «я — на рабочем месте», никакой иерархической структуры нет. Основной логической единицей, образующей иерархию, является план, а цели образуют иерархию лишь постольку, поскольку они являются элементами плана.
Американские психологи Дж.Миллер, Е.Галантер и К.Прибрам в своей книге «Планы и структура поведения» принимают понятие плана в качестве основы описания поведения человека и животных. Они показывают особенность и плодотворность такого подхода. В отличие от классической рефлекторной дуги (без обратной связи) логическая единица описания поведения, используемая этими авторами, содержит петлю обратной связи (рис. 2.10). Эту единицу они называют схемой T-O-T-E, по начальным буквам английских слов test-operate-test-exit (проверка — операция — проверка — выход).
Проверка здесь означает проверку соответствия ситуации и цели. В случае несоответствия производится операция, в случае соответствия план считается выполненным, и система идет на «выход». В качестве примера ни рис. 2.11 показан план забивания гвоздя в доску, представленный в виде единицы T-O-T-E.
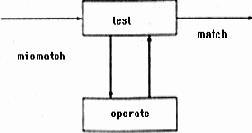
Рис. 2.10. ЕдиницаT-O-T-E (test-operate-test-exit)
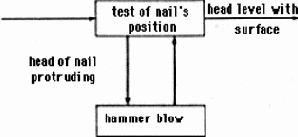
Рис. 2.11. Забивание гвоздя
Схема T-O-T-E на рис. 2.10 изображает то же самое явление регулирования, которое было изображено на рис. 2.6. Отличие между ними в способе изображения. Схема на рис. 2.6 — структурная, на рис. 2.10 — функциональная. Эти понятия надо пояснить. Заодно мы уточним понятие управления.
Иерархия понятий
На рис. 2.2 приведена схема классификатора, организованного по иерархическому принципу. Иерархия вообще — это такое построение системы из подсистем, когда каждой подсистеме приписывается определенное целое число, называемое ее уровнем, причем взаимодействие подсистем существенно зависит от разности их уровней, подчиняясь некоторому общему принципу. Обычно этот принцип — передача информации в определенном направлении (сверху вниз или снизу вверх) от данного уровня к следующему. В нашем случае рецепторам приписывается нулевой уровень, и информация распространяется снизу вверх. Каждая подсистема первого уровня связана с некоторым числом рецепторов, и ее состояние определяется состояниями соответствующих рецепторов. Точно так же каждая подсистема второго уровня связана с рядом подсистем первого уровня и т. д. На высшем (на схеме — четвертом) уровне находится одна выходная подсистема, которая и выносит окончательный приговор о принадлежности ситуации к тому или иному классу.
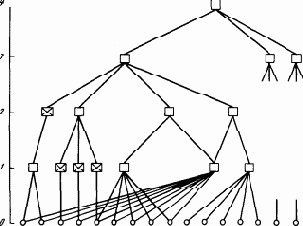
Рис. 2.2. Иерархия классификаторов
Из этого определения, которое трудно назвать шедевром ясности мысли, можно все-таки заключить, что общие понятия, которые образуются не путем перечисления единичных объектов, входящих в него, а путем указания ряда признаков, объявляемых существенными, и отвлечения от остальных (несущественных) признаков, можно также считать абстрактными. Мы будем рассматривать только такие общие понятия и будем называть их также абстрактными. Например, абстрактный треугольник — это любой треугольник, независимо от величины его сторон и углов и его положения на экране, следовательно, это абстрактное понятие. Такое употребление термина «абстрактный» имеет место в обиходе, а также в математике. В то же время, согласно учебнику логики, «треугольник», «квадрат» и т. п. суть конкретные общие понятия, а вот «треугольность» и «квадратность», которые им свойственны, это понятия абстрактные. По существу, здесь в ранг логического возводится чисто грамматическое различие, ибо даже с точки зрения сторонника последнего варианта терминологии обладание абстрактным понятием равнозначно обладанию соответствующим общим понятием.
Все подсистемы промежуточных уровней также являются классификаторами. Непосредственным входом k-го уровня служат состояния классификаторов k-1-го уровня, совокупность которых является для него ситуацией, подлежащей классификации. В иерархической системе, содержащей более одного промежуточного уровня, можно выделить иерархические подсистемы, охватывающие несколько уровней. Например, в качестве входных ситуаций для классификатора третьего уровня можно рассматривать состояния всех связанных с ним классификаторов первого уровня. Иерархические системы можно достраивать «вширь» и «ввысь» подобно тому, как из восьми кубиков можно сложить кубик с вдвое большим ребром, а из этих кубиков — еще больший кубик и т. д.
Так как с каждым классификатором связана система понятий, иерархия классификаторов порождает иерархию понятий. Передаваясь от уровня к уровню, информация преобразуется, выражаясь в терминах все более «высокопоставленных» понятий. При этом количество передаваемой информации постепенно уменьшается за счет отбрасывания информации, несущественной с точки зрения задачи, поставленной перед «верховным» (выходным) классификатором.
Поясним этот процесс на примере картинок, изображенных на рис. 2.1. Пусть поставлена задача распознавания «домиков». Введем два промежуточных понятийных уровня. На первом разместим совокупность понятий «отрезки», на втором — понятия «многоугольники». Понятие «домик» окажется на третьем уровне.
Под понятием «отрезки» мы понимаем совокупность понятий «отрезок с координатами концов x1, y1 и x2, y2», где числа x1, y1, x2, y2 могут принимать любые совместимые с устройством экрана и системой координат значения. Чтобы быть конкретнее, допустим, что экран содержит 1000 × 1000 светочувствительных точек. Тогда координатами могут служить десятиразрядные двоичные числа (210 = 1024 > 1000), а отрезок с заданными концами требует для своей характеристики четыре таких числа, т. е. 40 двоичных разрядов. Всего, следовательно, существует 240 таких понятий.
Их-то и должны различать классификаторы первого уровня.
Не надо думать, что отрезок с заданными концами — конкретное понятие, т. е. множество, состоящее из одной картинки. Классифицируя предъявленную картинку как отрезок с заданными концами, мы отвлекаемся от незначительных искривлений линии, вариаций ее толщины и т. п. (см. рис. 2.1). Критерий того, какие отклонения от нормы нам следует считать незначительными, может устанавливаться по-разному. Сейчас это нас не интересует.
Каждый классификатор первого уровня должен иметь на выходе подсистему из 40 двоичных разрядов, на которых «записаны» координаты концов отрезка. Сколько нужно классификаторов? Это зависит от того, какие картинки ожидаются на входе системы. Допустим, что для описания любой картинки достаточно 400 отрезков. Значит, достаточно 400 классификаторов. Разделим этот экран на 400 квадратов (50 × 50 точек) и свяжем с каждым квадратом классификатор, который будет фиксировать ближайший к нему, в каком-то смысле (детали разделения труда между классификаторами несущественны), отрезок. Если отрезка нет, пусть классификатор принимает какое-то стандартное «бессмысленное» состояние, например: все четыре координаты равны 1023.
Если предъявить нашей системе картинку, на которой изображено сколько-то отрезков, то соответствующее число классификаторов первого уровня укажет координаты концов отрезков, а остальные примут состояние «нет отрезка». Это и есть описание ситуации в терминах понятий «отрезки». Сравним количество информации на нулевом и на первом уровнях. На нулевом уровне нашей системы 1000 × 1000 = 106 рецепторов получают информацию в миллион бит. На первом уровне 400 классификаторов, каждый из которых содержит 40 двоичных разрядов, т. е. 40 бит информации, всего 16 000 бит. При переходе на первый уровень количество информации уменьшилось в 62,5 раза. Система сохранила ту информацию, которую она сочла «полезной» и отбросила информацию «бесполезную» с ее точки зрения. Относительность этих понятий видна из того, что если предъявленная картинка не соответствует иерархии понятий системы распознавания, то реакция системы будет неправильной или просто бессмысленной.
Если, например, на картинке более 400 отрезков, то не все отрезки будут зафиксированы, а если предъявить картинку с пятном, то реакция на нее будет такая же, как на пустую картинку.
Совокупность понятий «многоугольники», занимающую второй уровень иерархии, мы делим на две меньших совокупности: равнобедренные треугольники и параллелограммы. Из числа параллелограммов мы выделяем в особую совокупность прямоугольники. Считая, что для задания угла и длины надо столько же бит (10), как и для координаты, находим, что для задания определенного равнобедренного треугольника надо 50 бит информации, параллелограмма — 60 бит, прямоугольника — 50 бит. Соответственно этому должны быть сконструированы классификаторы второго уровня. Легко видеть, что вся нужная им информация имеется в наличии на первом уровне. Наличие многоугольника констатируется при наличии нескольких отрезков, находящихся между собой в определенных отношениях. При переходе на второй уровень происходит дальнейшее сжатие информации. Отводя из полного числа 400 отрезков по одной трети на каждый вид многоугольников, получаем систему, способную зафиксировать 44 треугольника, 33 прямоугольника и 33 параллелограмма (одновременно). Ее информационная емкость 5830 бит, т. е. почти втрое меньше, чем емкость первого уровня. Зато перед неправильным треугольником или четырехугольником система встанет в тупик!
Понятие «домик» легко описать на языке понятий второго уровня. Домик состоит из четырех многоугольников: одного прямоугольника, одного равнобедренного треугольника и двух параллелограммов, находящихся в определенных отношениях друг к другу (основание равнобедренного треугольника совпадает с одной стороной прямоугольника и т. д.).
Во избежание недоразумений следует указать, что иерархия понятий, о которой мы говорим, имеет гораздо более общий смысл, чем иерархия понятий по абстрактности (общности), которую часто называют просто «иерархия понятий». Примером иерархии по общности может служить пирамида понятий, относящихся к систематике животных.На нулевом уровне располагаются отдельные особи животных («конкретные» понятия), на первом — виды, на втором — роды, затем — семейства, отряды, классы, типы. На вершине пирамиды находится понятие «животное». Такая пирамида является частным случаем иерархии понятий в общем смысле, отличающимся тем, что каждое понятие k-го уровня образуется из некоторого числа понятий k-1-го уровня путем их объединения. Это соответствует очень просто устроенным классификаторам. В общем случае классификаторы могут быть устроены как угодно. Распознаватели, нужные животному, — это скорее иерархии по сложности и тонкости понятий, а не по общности.
Иерархия теорий
Осознание принципа описания действительности с помощью формализованного языка порождает, как мы видели, эффект лестницы. Вот пример лестницы из трех ступенек. Арифметика — это теория, которую мы применяем непосредственно к таким объектам неязыковой реальности, как яблоки, овцы, рубли, килограммы товаров. По отношению к ней школьная алгебра является метатеорией, которая знает лишь одну реальность — числа и числовые равенства, а ее буквенный язык — это метаязык по отношению к языку цифр арифметики. Современная аксиоматическая алгебра является метатеорией по отношению к школьной алгебре. Она имеет дело с некоторыми объектами (природа которых не уточняется) и некоторыми операциями над этими объектами (природа операций также не уточняется). Все выводы делаются из свойств операций. В приложениях аксиоматической алгебры к проблемам, сформулированным на языке школьной алгебры, объекты интерпретируются как переменные, а операции — как арифметические действия. Но современная алгебра с не меньшим успехом применяется и к другим ветвям математики, например к анализу или геометрии.
Углубленное изучение математической теории порождает новые математические теории, которые рассматривают исходную теорию в ее различных аспектах. Следовательно, каждая из этих теорий в некотором смысле проще (фундаментальнее), чем исходная теория, подобно тому, как исходная теория проще, чем действительность, которую она рассматривает всегда лишь в каком-то одном аспекте. Происходит расщепление моделей, выделение из сложной модели набора более простых моделей. Формально новые теории столь же универсальны, как исходная теория: их можно применять к любым объектам, которые удовлетворяют аксиомам независимо от их природы. При аксиоматическом подходе различные математические теории образуют, строго говоря, не иерархию по управлению, а иерархию по сложности. Однако, рассматривая те модели, которые на самом деле выражают законы природы (т. е. используются в приложениях математики), мы видим, что математические теории вполне отчетливо делятся на уровни сообразно характеру объекта, к которому они в действительности применяются.
Арифметика и элементарная геометрия непосредственно контактируют с неязыковой действительностью, а какая-нибудь теория групп используется для создания новых физических теорий, из которых извлекаются следствия, выраженные на языке алгебры и анализа, которые затем «доводятся до числа» и только после этого сравниваются с экспериментом. И это распределение теорий по уровням соответствует в целом тому порядку, в котором они возникали исторически, ибо возникали они путем последовательных метасистемных переходов. Ситуация здесь в сущности такая же, как и в иерархии орудий производства. Ведь и отверткой можно при желании ковырять землю. Однако изобретена она была не для того и нужна в действительности лишь тому, у кого есть винты, болты или шурупы. Теорию групп можно иллюстрировать простыми примерами из обыденной жизни или элементарной математики, но по-настоящему ее используют лишь математики и физики-теоретики. Продавцу в магазине или инженеру-практику теория групп нужна не больше, чем отвертка первобытному человеку.
Игра
Высшие животные обнаруживают одну интересную форму поведения, которая роднит их с людьми и является своего рода провозвестником приближения эры разума. Речь идет не о поведении, связанном со спариванием (которое также иногда называют игрой), а о «чистой» и, по видимости, совершенно бесцельной игре, игре для удовольствия. Так играет кошка с бумажкой, играют друг с другом детеныши всех млекопитающих, а также и взрослые животные.
Что же такое игра? Как возникает это явление в животном мире?
Обычно игру объясняют потребностью в тренировке мышц и нервной системы. Несомненно, что игра оказывает в этом смысле положительное влияние, т. е. она полезна. Однако недостаточно указать на полезность формы поведения, надо еще объяснить, как она становится возможной. Когда котенок играет с бумажкой на нитке, он ведет себя так, как будто он принимает ее за добычу. Но было бы недооценкой умственных способностей котенка полагать, что он всерьез заблуждается. Нет, он уже много раз ловил эту бумажку, кусал ее, ощущал ее противный, несъедобный запах. Представление котенка о бумажке не включается в понятие «добыча». Между тем это представление частично активизирует тот самый план действий, который нормально активизируется понятием «добыча». Точно так же волк, играющий с товарищем, вовсе не принимает его за врага, но ведет себя — до определенной черты — так, как будто перед ним враг. В этом вся сущность игры. Ее можно понять как произвольное установление ассоциации между двумя предметами: бумажка — добыча, товарищ — враг. В результате возникает новое представление, которому, строго говоря, нет эквивалента в реальности. Такое представление мы называем фантазией, плодом воображения. Это бумажка, которая, с одной стороны, явно не есть добыча и в то же время как будто бы и добыча; это товарищ, который одновременно и товарищ и враг.
Синтетическое представление порождает и синтетический план действий, игровой план. Волк вполне серьезно, изо всех сил, старается догнать и вцепиться в товарища, но кусает его уже не всерьез.
Да, игра тренирует мышцы, вырабатывает навыки, которые пригодятся при действиях всерьез. Но это скорее производит впечатление полезного побочного результата, чем специальной стратегической цели, ради которой развиваются игровые формы поведения. Хорошо известно, как любят играть дети. Но в игре их привлекает не только и даже не столько удовольствие от физического упражнения или проявления своей ловкости, сколько игра как таковая. Когда мальчики играют в солдатиков, а девочки в куклы, они ничего не тренируют, кроме своего воображения, т. е. способности произвольного ассоциирования. От этих-то произвольных ассоциаций они и получают удовольствие. Детская игра — фаза развития, через которую неизбежно должен пройти каждый человек, чтобы стать человеком. К.Чуковский в своей замечательной книге «От двух до пяти» много страниц посвящает развитию мысли об абсолютной необходимости элементов игры и фантазии в воспитании ребенка. Дети не могут обойтись без них, они нужны им, как воздух. Дети предаются игре со всем жаром, ощущая ее как нечто нужное, важное, серьезное. К.Чуковский пишет:
Я знал мальчугана, который, играя в трубочиста, воскликнул:
– Не трогай меня, мама, ты запачкаешься!.. И другого, который по ходу игры надолго превратился в котлету и, добросовестно шипя на сковороде, в сердцах оттолкнул свою мать, когда она бросилась к нему с поцелуями:
– Как ты смеешь целовать меня жаренного!
Чуть моя трехлетняя Мура, играя, разложила на полу свои книги, книги тотчас же сделались речкой, где она ловила рыбу и стирала белье. И, нечаянно наступив на одну книгу, она так естественно всхлипнула «Ой, я замочила себе ногу», что и я на секунду поверил, будто эти книги — вода, и чуть не бросился к ней с полотенцем.
Во всех этих играх ребята выступают как авторы и в то же время исполнители сказок, воплощающие их в сценических образах. И жажда верить в свой сказочный вымысел у них так велика, что всякая попытка поставить их в рамки действительности вызывает у них жаркий протест.
Через потребность в игре аппарат управления ассоциациями впервые заявляет о своем присутствии.И поскольку он существует, он должен работать, он требует себе дела. Это так же естественно, как то, что легкие требуют воздуха, а желудок — пищи.
Информация
Начав описывать конкретную кибернетическую систему, мы невольно употребляем термин информация, который в своем разговорном, неформальном значении хорошо знаком и понятен каждому культурному человеку. Теперь мы введем кибернетическое понятие информации, имеющее точный количественный смысл.
Представим себе две подсистемы A и B (рис. 1.2), связанные между собой таким образом, что изменение состояния системы A влечет изменение состояния системы B. Это можно выразить такими словами: подсистема A воздействует на подсистему B.
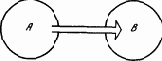
Рис. 1.2. Связанные подсистемы
Рассмотрим подсистемы B в некоторый момент времени t1
и в более поздний момент времени t2. Первое обозначим через S1, второе — через S2. Cостояние S2 зависит от состояния S1. Однако оно не определяется состоянием S1
однозначно, а зависит от него вероятностным образом, ибо мы рассматриваем не идеализированную теоретическую систему, подчиняющуюся детерминистическому закону движения, а реальную систему, состояния которой S суть результаты опытных данных. При таком подходе тоже можно говорить о законе движения, понимая его в вероятностном смысле, т. е. как условную вероятность состояния S2
в момент t2 при условии, что в момент t1
система имела состояние S1. Теперь забудем на минуту о законе движения. Обозначим через N полное число возможных состояний подсистемы B
и будем представлять себе дело таким образом, что в любой момент времени подсистема B может с равной вероятностью принять любое из N
состояний независимо от того, какое состояние она имела в предыдущий момент. Попытаемся количественно выразить степень (или силу) причинно-следственного влияния подсистемы A на такую безынерционную и «беззаконную» подсистему B. Пусть B под действием A переходит в некоторое совершенно определенное состояние. Ясно, что «сила влияния», которая требуется для этого от A, зависит от числа N и тем больше, чем больше N. Если, например, N = 2, то система B, даже будучи совершенно не связана с A, под действием каких-то случайных причин может с вероятностью 1/2
перейти в то самое состояние, которое «рекомендует» система A.
Если же N
= 109, то, заметив такое совпадение, мы вряд ли усомнимся во влиянии A на B. Следовательно, мерой «силы влияния» A на B
в данном единичном акте, т. е. по существу мерой интенсивности причинно-следственной связи между двумя событиями — состоянием подсистемы A
в интервале времени от t1 до t2 и состоянием подсистемы B в момент t2 — должна служить какая-то монотонно возрастающая функция N. В кибернетике эта мера называется количеством информации, переданной от A к B между моментами времени t1 и t2, а монотонно возрастающей функцией служит логарифм. Итак, в нашем примере количество информации I, переданное от A к B, равно log N.
Выбор логарифмической функции определяется тем ее свойством, что
log N1
N2 = log N1 + log N2.
Пусть система A действует на систему B, состоящую из двух независимых подсистем B1 и B2 с возможным числом состояний N1 и N2 соответственно (рис. 1.3). Тогда число состояний системы B есть N1×N2, а количество информации I, которое надо передать системе B, чтобы она приняла одно определенное состояние, есть благодаря указанному свойству логарифма сумма
I = log N1 N2 = log N1
+ log N2 = I1 + I2,
где I1 и I2 — количества информации, потребные подсистемам B1 и B2. Благодаря этому свойству информация принимает определенные черты субстанции, она распределяется по независимым подсистемам подобно жидкости, разливающейся по сосудам. Мы говорим о слиянии и разделении информационных потоков, об информационной емкости, о переработке информации и ее хранении.
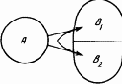
Рис. 1.3. Воздействие на две независимые подсистемы
Вопрос о хранении информации связан с вопросом о законе движения. Выше мы мысленно отключили закон движения, чтобы определить понятие передачи информации. Если мы теперь рассмотрим закон движения с новой точки зрения, то он сводится к передаче информации от системы B в момент времени t1 к той же самой системе B в момент t2. Если состояние системы не меняется с течением времени, то это и есть хранение информации.
Если состояние S2 однозначно определяется состоянием S1 в предыдущий момент времени, то систему называют полностью детерминированной. Если имеет место однозначная зависимость S1 от S2, то систему называют обратимой; для обратимой системы можно, в принципе, по заданному состоянию вычислить все предыдущие состояния, поэтому потери информации не происходит. Если система необратима, информация теряется. Закон движения в сущности есть нечто, регулирующее поток информации во времени от системы к ней самой.
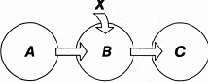
Рис. 1.4. Канал связи
На рис. 1.4 изображена схема передачи информации от системы A к системе C через систему B. Эта последняя носит название канала связи. На состояние B может влиять не только состояние системы A, но еще какой-либо не поддающийся контролю фактор X, называемый помехой. Конечное состояние системы C в этом случае зависит не только от состояния A, но и от фактора Х (искажение информации). Еще одна важная схема обмена информации изображена на рис. 1.5. Это так называемая схема обратной связи. Состояние системы A в момент времени t1 влияет на состояние B в момент времени t2, а это последнее влияет на состояние системы A в момент времени t3. Путь информации замыкается.
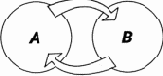
Рис. 1.5. Обратная связь
На этом мы пока ограничим наше знакомство с общими понятиями кибернетики и вернемся к эволюции жизни на Земле.
Интеграция и свобода
Процесс социальной интеграции никогда еще не протекал так бурно и так явно, как сейчас. Современные наука и техника сделали каждого человека находящимся в сфере влияния каждого другого. Современная культура глобальна. Современные государства — это огромные механизмы, имеющие тенденцию все более жестко регламентировать поведение каждого гражданина, определять, навязывать ему извне его потребности, вкусы, мнения. Современного человека преследует ощущение, что он превращается всего лишь в стандартизованный винтик этого механизма, что он перестает существовать как личность.
Поэтому сейчас мы лучше, чем когда бы то ни было, видим основное противоречие социальной интеграции — противоречие между необходимостью включить человека в систему, в непрерывно консолидирующееся целое, и необходимостью сохранить его как свободную творческую личность. И здесь возникает важнейшая, фундаментальнейшая проблема: разрешимо ли это противоречие? Возможно ли общество, которое, идя все дальше по пути интеграции, будет в то же время обеспечивать полную свободу проявления личности? Эта проблема стоит перед современностью во весь рост, и различное ее решение дает различные концепции общества.
Оптимистический ответ на поставленный вопрос звучит утвердительно. Каждый следующий этап интеграции общества, гласит этот ответ, будет, вероятно, сопряжен с какими-то внешними ограничениями, несущественными с точки зрения творческой деятельности, но зато будет способствовать освобождению ядра личности, являющегося источником творчества. Вера в возможность такого общества равнозначна вере в то, что импульс, заложенный природой в человека, не исчерпан, что человек способен продолжать начатый им этап космической эволюции. Ведь личностное, творческое начало является сущностью человека, основным двигателем эволюции в эпоху разума. Если оно будет подавлено социальной интеграцией, то движение остановится. С другой стороны, и социальная интеграция необходима. Без нее невозможно дальнейшее развитие культуры, увеличение власти человека над природой; в ней — сущность нового уровня организации материи.
Почему же мы должны полагать, что социальная интеграция и свобода личности несовместимы? Ведь осуществлялась же интеграция успешно на других уровнях организации! Когда клетки объединяются в многоклеточный организм, то свои биологические функции — обмен веществ и размножение путем деления — они продолжают выполнять. Новое качество — жизнь организма появляется не вопреки биологическим функциям отдельных клеток, а, напротив, благодаря им. Творческий акт свободной воли — это «биологическая» функция человеческой личности. Следовательно, в интегрированном обществе она должна сохраниться в качестве неприкосновенной основы, а новые качества должны появляться лишь через нее и благодаря ей.
Если мы откажемся от веры в возможность органического сочетания социальной интеграции и свободы личности, то должны будем одно из них предпочесть другому. Предпочтение свободы личности приводит к индивидуалистической концепции общества, предпочтение социальной интеграции — к тоталитарным режимам.
Индивидуализм рассматривает общество лишь как способ «мирного сосуществования» индивидуумов, и увеличения личных благ для каждого из них. Но эта идея сама по себе недостаточна для построения здорового общества. Чистый индивидуализм лишает жизнь человека всякого высшего смысла и влечет цинизм и духовное оскудение. Фактически индивидуализм существует только благодаря союзу с традиционными религиозными системами или, лучше сказать, благодаря паразитированию на них, ибо они в принципе враждебны индивидуализму и допускают его по слабости. С разрушением религиозных систем это паразитирование достигает огромных размеров, индивидуализм становится страшной язвой, разъедающей общество, и он неминуемо, как протест против себя, порождает свое отрицание — тоталитаризм.
Для тоталитаризма — интеграция все, личность — ничто. Он строит иерархическую государственную систему, во главе которой стоит, как правило, один человек или небольшая группа людей. Строится также идеологическая система, которую каждый гражданин обязан принять в качестве личного мировоззрения.
Кто отказывается это сделать, подлежит наказанию, вплоть до физического уничтожения.
Человек, зажатый между этими двумя системами, превращается в бездумную и бездушную деталь социальной машины. Ему представляется лишь та свобода, которая необходима для выполнения инструкций вышестоящих инстанций. Всякое проявление личностной деятельности рассматривается как потенциально опасное для государства. Права личности аннулируются.
Тоталитарное государство, стремясь сохранить и упрочить себя, использует все средства физического и нравственного воздействия на человека, чтобы сделать его пригодным для себя, «тоталитарным» человеком. Основное свойство тоталитарного человека — это наличие для него определенных запретов, табу, нарушить которые он не в состоянии. Он может быть ученым, пытливым исследователем, но при подходе к определенным сторонам жизни его пытливость начнет вдруг таинственным образом испаряться. Он может быть отважным человеком, способным, не задумываясь, отдать жизнь за свою родину, но трепетать от страха перед начальником. Он может считать себя честным человеком и говорить заведомую ложь, не желая связать этот факт со своей мнимой честностью. Он может грабить, предавать, убивать, будучи уверенным, что «так надо», но он никогда не позволит себе всерьез задуматься над вопросом: «А надо ли?». И он будет за версту обходить все, что может заставить его задуматься над этим.
Чем же компенсирует тоталитарный человек эти табу, налагаемые как раз на то, что составляет высшую ценность человеческого существования? Чувством единства. Ощущением своей принадлежности к огромной совокупности людей, организованных в единое целое. Человеческому существу свойственна внутренняя потребность в социальной интеграции. В том-то и сила тоталитаризма, что он играет на этой потребности, дает ей определенное удовлетворение. Сила и опасность тоталитаризма в том, что он — за социальную интеграцию, а социальная интеграция есть объективная необходимость.
Но тоталитарное государство не является решением проблемы социальной интеграции.
Оно достигает целостности путем такого обтесывания составляющих его единиц — людей, что они теряют свою человеческую сущность. Он отрубает людям головы и заставляет обрубки упиваться достигнутым такой ценой единством.
Тоталитаризм — трагически неумелое и поспешное псевдорешение проблемы, это выкидыш социальной интеграции. Уничтожив личность, он лишает себя источника творчества. Он обречен на загнивание и распад.
Если индивидуализм порождает тоталитаризм, то и тоталитаризм, обратным путем, порождает индивидуализм. «Долой коллектив! — кричит тоталитарный человек, осознавший свое рабство. — Оставьте меня в покое! Не хочу единства! Не хочу стальных рядов! Не хочу чувства локтя! Хочу жить так, как Я хочу! Я! Я! Я!» Но кричит он это, опасаясь наказания, мысленно или, в лучшем случае, шепотом. Его «Я», выросшее в условиях тоталитаризма, — это убогое, полузадушенное «Я». И он превращается в никчемного обывателя с куриным кругозором. Его не интересует ничего, кроме его персоны. Он не верит ни во что и поэтому всему подчиняется. Это уже не тоталитарная личность, а жалкий и трусливый индивидуалист, живущий в тоталитарном государстве.
Индивидуализм и тоталитаризм — две противоположности, связанные общей цепью. Есть только один способ разорвать этот круг: ставить своей задачей сознательную социальную интеграцию при сохранении и развитии творческой свободы личности.
Италия, XVI век
В первой половине XVI в. благодаря усилиям итальянских математиков в алгебре происходят крупные сдвиги, сопровождаемые весьма драматическими событиями. Профессор Болонского университета Сципион Даль Ферро (1465–1526) находит общее решение уравнения третьей степени
х3 + рх = q
при положительных р и q, но держит его в секрете, ибо оно представляет большую ценность на соревнованиях по решению задач, которые тогда широко практиковались в Италии. Перед смертью он открывает секрет своему ученику Фиоре. В 1535 г. Фиоре вызывает на соревнование талантливейшего математика Никколо Тарталью (1499–1557), который, зная, что Фиоре обладает способом решения кубического уравнения, прилагает максимум усилий и сам находит решение! Тарталья побеждает на соревновании, но также держит свое открытие в секрете. Наконец, на сцене появляется Джероламо Кардано (1501–1576). Он тщетно пытается найти алгоритм решения кубического уравнения и в 1539 г. обращается к Тарталье с просьбой поведать ему тайну. Взяв с Кардано «священную клятву» молчания, Тарталья частично и в не слишком вразумительной форме приоткрывает для него завесу. Кардано не удовлетворяется и прилагает усилия, чтобы ознакомиться с рукописью покойного Даль Ферро. Это ему удается, и в 1545 г. он публикует книгу, в которой сообщает алгоритм, сводящий решение кубического уравнения к радикалам («формула Кардано»). В этой же книге содержится еще одно открытие, сделанное учеником Кардано Луиджи (Лудовико) Феррари (1522–1565), а именно решение в радикалах уравнения четвертой степени. Тарталья обвиняет Кардано в нарушении клятвы, завязывается острая и продолжительная полемика. При таких обстоятельствах заявляет о своих первых существенных достижениях математика Нового времени.
Использование инструмента подсказывает пути к его усовершенствованию. Стремясь к единообразному решению уравнений, математики обнаружили, что для достижения этой цели чрезвычайно полезно внести некоторые новые объекты и обращаться с ними так, как если бы это были числа.
Их и называют числами, хотя понимают, что они отличаются от «настоящих» чисел; это проявляется в том, что им придают такие эпитеты, как «ложные», «фиктивные», «непостижимые», «мнимые». Чему они соответствуют в действительности, остается не совсем ясным или совсем неясным. Законно ли их использование, тоже остается спорным. Тем не менее, их используют все шире, ибо с их помощью получаются конечные результаты, которые содержат лишь «настоящие» числа и которые нельзя получить иначе. Человек, последовательно придерживающийся учения Платона, не мог бы использовать «ненастоящие» числа. Однако индийские, арабские и итальянские математики отнюдь не были последовательными платониками; здоровое любопытство и прагматические соображения перевешивали для них теоретическую недозволенность. Правда, при этом они все-таки делали оговорки и как бы извинялись за свое «некорректное» поведение.
Все «ненастоящие» числа — продукт обратного хода арифметической модели, они формально являются решениями таких уравнений, которые не имеют решения в области «настоящих» чисел. В первую очередь надо назвать отрицательные числа. Мы находим их уже в довольно развитом виде у индийского математика Бхаскары (XII в.), который совершает над ними все четыре действия арифметики. Интерпретация отрицательного числа как долга (в противоположность имуществу) была известна индусам еще в XII в. Бхаскара, формулируя правила действий над отрицательными числами, называет их «долг», а положительные — «имущество». Объявить отрицательное число таким же абстрактным понятием, как положительное число, он не решается. «Люди не одобряют отвлеченных отрицательных чисел», — пишет Бхаскара. Примерно так же относятся к отрицательным числам и в Европе XV–XVI вв. При геометрической интерпретации отрицательные корни называют «ложными» в отличие от «истинных» положительных корней. Современная интерпретация отрицательных чисел как точек, лежащих левее точки нуль, появилась только в «Геометрии» Декарта (1637 г.). По традиции Декарт называл отрицательные корни «ложными».
Формальные действия над корнями из чисел, которые не извлекаются в точном виде, восходят к глубокой древности, когда еще не было понятия о несоизмеримости отрезков. В XV–XVI вв. с ними обращаются совсем запросто — помогает здесь, конечно, простая геометрическая интерпретация. Понимание теоретической трудности, вытекающей из несоизмеримости отрезков, проявляется в названии этих чисел: «иррациональные», т. е. не постижимые разумом.
Квадрат любого числа положителен, поэтому квадратного корня из отрицательного числа не существует среди положительных, отрицательных, рациональных или иррациональных. Однако Кардано осмелел настолько, что стал формально оперировать (не без оговорок) с корнями из отрицательных чисел. Так в XVI в. возникли самые невозможные из всех невозможных чисел — «мнимые». Логика использования алгебраического языка неудержимо влекла математиков по неизведанному пути. Он казался незаконным и таинственным, но интуиция подсказывала, что все эти невозможные числа имеют глубокий смысл и новый путь себя оправдает. Так оно и оказалось.
Изготовление орудий
Однако оставим игры и перейдем к серьезным поступкам взрослых людей.
Говоря о происхождении человека, в качестве первого его отличия от животного указывают на использование и изготовление орудий. Решающим здесь является, конечно, изготовление орудий. Использовать предметы в качестве орудий могут и животные. Дятловый вьюрок с Галапагосских островов с помощью колючки кактуса или щепочки выковыривает червяков из коры дерева. Каждый, кто видел на кинокадрах, как ловко управляется вьюрок с зажатой в клюве колючкой, не может не согласиться, что это явное и весьма искусное использование орудия. Калифорнийская морская выдра ложится на спину на поверхности воды, кладет себе на грудь плоский камень и разбивает об него ракушки. Обезьянам случается пользоваться палкой и камнем. Эти примеры чрезвычайно скудны, однако они показывают, что принципиально в использовании животным орудий нет ничего невозможного. В самом деле, почему план действий, передаваемый по наследству и подкрепляемый обучением, не может включать выбора и использования определенного рода предметов? Ведь такие понятия, как «длинное, острое» или «округлое, тяжелое», вполне доступны животному. Очевидно, примеры, подобные приведенным выше, редки потому, что орудия, которые можно получить от природы без специального изготовления, весьма несовершенны, и животные с большим успехом используют и совершенствуют в процессе эволюции свои естественные органы: клюв, когти, зубы. Чтобы использование орудий стало не исключением, а правилом, надо уметь изготовлять или хотя бы находить подходящие предметы ad hoc, т. е. специально для данного конкретного случая.
Допустим, вам надо забить гвоздь, а у вас под рукой нет молотка. Вы оглядываетесь, ища подходящий предмет, и видите на столе бронзовый бюст Наполеона. Раньше вам никогда не приходилось заколачивать гвозди наполеонами. Можно даже допустить, что ничем, кроме настоящего молотка, вы гвоздей не забивали. Это не помешает вам взять бюст и забить гвоздь. Ассоциации гвоздь — бюст у вас не было. Вы ее создали заново и ad hoc. Вы сопоставили в своем воображении гвоздь и бюст Наполеона, представили, как вы забиваете им гвоздь, и осуществили это на деле.
Язык
До сих пор мы рассматривали человека как индивидуума и интересовались возможностями его мозга. При таком подходе вовсе не очевидно, что появление на Земле человека — это такая уж революция в истории жизни. Лягушка умнее медузы. Собака умнее лягушки. Обезьяна умнее собаки. Теперь появилось существо, которое умнее обезьяны. Ну и что?
Революцию создало появление человеческого общества, обладающего определенной культурой и, в первую очередь, языком. Ключевым моментом является здесь язык.
Под языком вообще понимают определенный способ сопоставления объектам Ri, которые рассматриваются как некая первичная реальность, объектов Li, называемых именами объектов Ri, и рассматриваемых как нечто вторичное, специально созданное для сопоставления объектам Ri,. По отношение к имени Li объект Ri, называют его значением. Совокупность всех объектов Li часто также называют языком (в более развернутой форме ее следовало бы назвать материальным фиксатором или носителем языка). Множество объектов Li, может быть гораздо обширнее и разнообразнее множества языков Li. Так, например, обстоит дело в случае естественных языков: русского, английского и т. п. Ясно, что при замене восприятия реальных объектов и ситуаций на их словесное описание теряется огромное количество информации. В тех случаях, когда информативность объектов Ri и Li одного порядка величины, вместо слова язык часто употребляют кибернетический термин код. Переход от R к L называют кодированием, а обратный переход от L к R — декодированием. Так, при передаче по радио сообщения с помощью «морзянки», исходный текст — набор букв кодируется набором точек и тире. В этом коде (языке) информация совершает путешествие в эфире и принимается в заданной точке. Затем происходит декодирование с языка точек и тире на язык букв. Процесс кодирования и декодирования в данном случае не приводит к потере информации.
Так как для перехода от значения к имени и обратно нет более удобных общепринятых терминов, чем кодирование и декодирование, мы будем употреблять эти термины в самом общем смысле, не заботясь о соотношении информативностей (и называя язык не «кодом», а именно «языком»).
Объекты Ri и Li могут быть произвольной природы, это не обязательно предметы, а, вообще говоря, явления, звуковые колебания. Заметим, что «явление» — это самый общий термин, которым мы можем обозначить какую-то часть физической реальности, ограниченную в пространстве и времени, «предмет» — более расплывчатое понятие, которое относят к явлениям специального типа, обнаруживающим определенную стабильность: наличие поверхности, через которую отсутствует обмен веществом. Так как в действительности абсолютно непроницаемых границ не существует, и все так называемые предметы непрерывно меняются, это понятие относительно; оно отражает лишь малую скорость изменений.
Элементарный язык есть и у животных, в первую очередь у тех, которые живут сообществами и поэтому должны как-то согласовывать свои действия и «выяснять отношения». Мы называем его элементарным лишь в сравнении с языком человека, сам по себе он не так уж прост и, по-видимому, прекрасно удовлетворяет потребность членов сообщества в обмене информацией. Сигнал опасности, просьба о помощи, намерение вступить в брачные отношения, согласие или отказ на это предложение, приказ подчиниться, приказ убраться восвояси — эти и другие компоненты входят в состав языка большинства птиц и млекопитающих и выражаются жестами и звуками. Пчелы, вернувшись с взятка в улей, сообщают родичам о расположении места, где они были, совершая своеобразные движения, напоминающие танец.
Язык как средство моделирования
Язык возникает как средство связи, коммуникации между членами первобытного сообщества. Но, раз возникнув, он вдруг оказывается источником других, совершенно новых возможностей, не связанных в принципе с общением между людьми. Что это за возможности, покажем на примере языка чисел.
Вообразим себе юношу из первобытного племени Ням-Ням. Назовем его для определенности Уу и проследим, как он выполняет функции разведчика.
Уу лежит за толстым старым дубом и неотрывно следит за входом в пещеру на противоположном берегу реки. На восходе солнца сюда подошла группа мужчин из вражеского племени Мань-Мань. Они явно затеяли что-то нехорошее, наверное, оставить в пещере засаду. Они суетятся около пещеры, то входят в нее, то выходят, то исчезают в лесу, то снова возвращаются к пещере. Каждый раз, когда один враг входит в пещеру, Уу загибает один палец, когда один враг выходит из пещеры, он разгибает один палец. Когда враги уйдут, Уу будет знать, оставили ли они засаду и если оставили, то сколько человек. Уу побежит к своему племени и покажет им на пальцах, сколько врагов осталось в пещере.
Почему наш герой имеет возможность, не заходя в пещеру, знать в каждый момент времени, сколько там врагов? Потому что с помощью своих пальцев он построил модель интересующей его части внешнего мира. А интересует его пещера и находящиеся в ней враги. Каждому врагу, находящемуся в пещере, соответствует в его модели загнутый палец. Загнутый палец — это имя
врага в пещере, враг в пещере — это значение загнутого пальца. Операции над именами — загибание и разгибание пальцев — соответствуют входу и выходу врагов из пещеры. Это — язык. Его можно назвать языком пальцев, если иметь в виду физический материал, из которого построена модель, или языком чисел, если иметь в виду способ сопоставления имен значениям. И этот язык используется не только, а в нашем примере даже не столько для передачи информации, сколько для построения модели, которая нужна именно как модель — средство предвидеть события, средство узнать косвенно то, что нельзя узнать прямо.
Если родное племя Ням-Ням далеко, а Уу не собирается никому сообщать, сколько врагов в пещере, он все равно имеет основания считать врагов, сгибая и разгибая пальцы. Это нужно ему самому для планирования своих действий. Коммуникативное использование языка, т. е. использование его как средства общения между людьми, дополняется некоммуникативным использованием языка в качестве средства построения моделей действительности.
Тут-то, как говорят англичане, лягушка и прыгает в воду. Моделирующая функция языка — тот заключительный элемент, которого нам не хватало для оценки появления на земле человека как рубежа двух эпох, как события космической важности. Когда астроном определяет положение планет на небе, затем производит какие-то манипуляции над цифрами и в результате предсказывает, где будут планеты через заданный промежуток времени, он делает в сущности то же самое, что юноша Уу из племени Ням-Ням, когда он загибает и разгибает пальцы, наблюдая за входом в пещеру. Искусство, философия, наука — все это не что иное, как создание языковых моделей действительности. Дальнейшая часть настоящей книги будет посвящена анализу этого процесса, его закономерностей и результатов. Но сначала мы бросим общий взгляд на его место в эволюции Вселенной.
Языкотворчество
Но язык у человека радикально отличается от языка у животных. Различие здесь такое же, как в употреблении орудий. Для животного язык есть нечто изначально данное, элемент инстинктивного поведения. Если он и меняется, то только вместе с поведением, вместе с общей эволюцией вида. Для человека язык — нечто несравненно более подвижное и изменчивое, чем поведение. Человек сам создает язык, он обладает способностью (и даже потребностью) давать имена, чего не может ни одно животное. Присвоение явлениям (в частности, предметам) имен — это, пожалуй, наиболее простое и наглядное проявление управления ассоциированием. Между словом «лев» и реальным львом нет ничего общего, тем не менее устанавливается ассоциация «лев» — лев, имя — значение. Правда, среди слов, появившихся на заре человеческой культуры, было много звукоподражательных. Это подтверждается обилием таких слов в языках примитивных культур.
То же в еще большей степени относится и к жестам. Жест, очевидно, всегда подражателен в своей основе. Но это не меняет природы ассоциации между именем и значением, как результат намеренного ассоциирования. Допустим, что в некотором примитивном языке лев называется «ррррр» — словом, имитирующим его рычание. Ассоциация «ррррр» — лев возникает не потому, что этот звук можно спутать с рычанием льва (хорош был бы охотник, способный допустить такую ошибку), а потому, что, подыскивая имя для льва, человек перебирает в воображении его особенности и останавливается на одной из них, как допускающей хотя бы приблизительное воспроизведение. Создатель имен воспринимает его субъективно как нечто близкое к значению, подобное ему, а точнее не подобное, а уподобленное, ибо объективная схожесть между именем и значением может быть невелика, почти равна нулю; она служит лишь пуповиной, отсыхающей вскоре после рождения имени. Ассоциация имя — значение возникает совсем не так, как ассоциация между видом миски и отделением слюны в опытах Павлова над собаками. Там условный рефлекс, здесь языкотворчество. Повод, послуживший для выбора имени, забывается, само имя трансформируется, но связь между именем и значением от этого ничуть не страдает.
Языковая деятельность
Среди всех представлений выделенное место в процессе мышления занимают представления о языковых объектах — словах и предложениях. Эти представления всегда (за исключением, конечно, глухонемых) являются единством слуховых и моторных представлений, а у людей, с детства имеющих дело с письменностью, к ним может присоединиться и зрительная компонента. Представляя в уме какое-либо слово, мы мысленно произносим его, слышим и, возможно, видим написанным. Будем для краткости называть их языковыми представлениями. Именно поток языковых представлений называют обычно мышлением. Наличие этого потока является специфической особенностью человека; у животных он отсутствует. Так называемое абстрактное мышление на деле — мышление словами, поток языковых представлений. Достижения мысли, которыми так гордится человечество, были бы невозможны без мышления словами.
Значение языковых представлений состоит в том, что они однозначно связаны со словами и предложениями как материальными элементами материальной системы «язык». Эта последняя система есть совокупность всех слов и предложений, произносимых устно, передаваемых по телефону и радио, написанных или напечатанных на бумаге, закодированных на перфокартах для вычислительных машин и т. д., — одним словом, то, что мы назвали выше нервной системой материального тела культуры. Функционально поток языковых представлений ничем не отличается от последовательности их материальных коррелятов — слов. Внешнюю, наблюдаемую сторону мышления можно описать как деятельность, состоящую в создании некоторых материальных языковых объектов, например, произнесение предложений вслух (к сожалению, эти объекты очень недолговечны) или написание их на бумаге. Такую деятельность мы будем называть языковой.
Есть веские основания именно языковую деятельность считать основной, первичной стороной мышления, а поток языковых представлений — лишь переходным элементом, формой связи между материальными языковыми объектами и совокупностью всех (а не только языковых) представлений.
В самом деле, ведь именно языковые объекты являются хранителями и передатчиками информации, а также элементами языковых моделей действительности. Ребенка обучают языковой деятельности подобно тому, как его обучают другим видам деятельности: хождению, стрельбе из лука, забиванию гвоздей. В результате он как бы подключается к языку, использует уже имеющиеся в нем модели и обогащает его новыми. В частности, он может использовать его и некоммуникативно («для себя»), как юноша Уу из племени Ням-Ням, который считал врагов по пальцам. При некоммуникативном использовании языка возможно наличие потока языковых представлений без явной деятельности («я думаю!»), но ведь эти представления возникли и приобрели смысл в результате деятельности с вещественными материальными языковыми объектами! И нередко в процессе размышления мы шепчем отдельные слова и целые фразы, возвращая им материальную оболочку. Первичность вещественной языковой деятельности особенно ясно видна, когда мы имеем дело с научными моделями действительности. Человек может в уме перемножить несколько больших чисел или привести подобные члены в несложном алгебраическом выражении, но это следствие того, что его учили делать это с реальными, написанными символами. Задайте ему задачу посложнее, и он потребует карандаш и бумагу!
Исследованием языковой деятельности занимаются лингвистика и логика. Лингвистику интересует главным образом синтаксис языков (в широком, семиотическом смысле), логику — семантика. Когда синтаксис и семантика сплетаются, невозможно отделить и лингвистику от логики. Правда, традиционная логика провозглашает себя наукой не о языке, а о законах мышления, но это претенциозное заявление не следует принимать слишком всерьез. Из всех разделов знания, изучающих мышление, подход логики самый внешний, поверхностный. Она не исследует реальных механизмов работы мозга, как нейрофизиология, не строит моделей умственной деятельности, как кибернетика, не пытается фиксировать и классифицировать субъективно воспринимаемые душевные состояния, как психология.
В качестве объекта изучения она признает лишь четкие, общественно значимые (а не бред сумасшедшего!) мысли. Но такие мысли на самом деле суть не что иное, как языковые представления с общественно значимой семантикой. Логический (семантический) анализ языка приводит к первичным неопределяемым понятиям и на этом кончается; он не выводит нас за пределы языка.
Логика содержит еще теорию доказательства. Если пользоваться языком не в его натуральном виде, а в виде записи, выдержанной в соответствии с каноном исчисления предикатов, то можно установить формальные признаки справедливости умозаключений, формальные правила, пользуясь которыми мы всегда из правильных предпосылок получим правильные заключения. Эти правила (законы логики), которые выражаются также в виде языкового объекта, образуют метасистему по отношению к высказываниям, получающимся в результате применения правил (рис. 7.1). Для теории доказательства предложения являются объектом и результатом работы. Таким образом, вся логика целиком лежит в сфере языковой деятельности. Ее нижний этаж — семантический анализ, верхний — теория доказательства. О теории доказательства речь впереди; пока нас интересует нижний этаж и даже фундамент — связь между языком и работой мозга.
Будем считать, что путем языкового анализа мы можем перевести любую фразу естественного языка на язык логики. Это, конечно, некоторое преувеличение достигнутых к настоящему моменту успехов, но довольно ясно, что в принципе здесь нет ничего невозможного. Логический анализ вскрывает внутреннюю структуру языка, фундаментальные узлы, из которых он состоит. Поэтому поставим себе задачу рассмотреть основные понятия языка логики и уяснить, почему они именно такие и каким образом они связаны с деятельностью мозга. В отличие от предыдущей главы, где речь шла преимущественно о синтаксисе языка, поставим вопрос о его семантике.
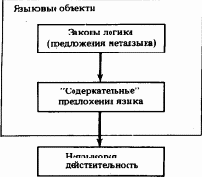
Рис. 7.1. Логика как метасистема
Языковая машина
Так как синтаксические преобразования L1 > L2 в рамках формализованного языка определяются только физическим видом объектов Li, формализованный язык есть, в сущности, машина, производящая различные перемещения символов. Для полностью алгоритмизированного языка, например арифметики, этот тезис представляется совсем очевидным и иллюстрируется существованием машин в обычном, узком смысле слова (арифмометр, электронная вычислительная машина), выполняющих арифметические алгоритмы. Если правила преобразования представляют собой лишь ограничения, то, во-первых, можно построить алгоритм, который по заданным L1 и L2 определяет, законно ли преобразование L1 > L2, во-вторых, можно построить алгоритм («глупый»), который по заданному L1 начинает выдавать все законные результаты L2 и продолжает этот процесс до бесконечности, если число возможных L2 не ограничено. В обоих случаях мы имеем дело с некоторой языковой машиной, которая может работать без вмешательства человека.
Формализация языка имеет два непосредственных следствия. Во--первых, упрощает процесс использования языковых моделей, ибо появляются четкие правила преобразования L1 > L2. В предельном случае полной алгоритмизации это преобразование вообще может производиться автоматически. Во-вторых, языковая модель становится независимой от создавшего ее человеческого мозга, она становится объективной моделью действительности. Ее семантика отражает, конечно, понятия, возникшие в процессе развития культуры человеческого общества, но и по синтаксису она представляет собой языковую машину, которая может продолжать работать и сохранять свой смысл модели действительности даже в том случае, если все человечество внезапно вымрет. Изучая эту модель, разумное существо, имеющее определенное представление о предмете моделирования, сможет, вероятно, путем сопоставления модели со своими знаниями, восстановить семантику языка. Представим себе, что люди построили механическую модель Солнечной системы, в которой планеты изображаются шариками соответствующих размеров, вращающимися на стерженьках вокруг центрального шара — Солнца по соответствующим орбитам и с соответствующими периодами. И допустим, что эта модель попала в руки (или в щупальца?) обитателей соседней звездной системы, которые кое-что знают о нашей Солнечной системе, например расстояния до Солнца нескольких планет или времена их обращения. Тогда они смогут сообразить, что находится перед ними, и получат дополнительные сведения о Солнечной системе. То же относится и к научным теориям, которые суть модели реальности в различных ее аспектах, выполненные в материале формализованного знакового языка. Подобно механической модели Солнечной системы каждая из них может быть, в принципе, расшифрована и использована любыми разумными существами.
Эффект лестницы
На нижней ступени гигантской каменной лестницы играет ребенок. Ступеньки высоки, и ребенок не может перебраться со своей ступеньки на следующую. Ему очень хочется посмотреть, что там делается; время от времени он пытается схватиться за край ступеньки и вскарабкаться на нее, но это ему не удается... Проходят годы. Ребенок растет и в один прекрасный день вдруг оказывается способным преодолеть это препятствие. Он забирается на манившую его ступеньку и видит, что выше есть еще одна ступенька, на которую он теперь тоже может залезть. Так, преодолевая ступеньку за ступенькой, он поднимается все выше и выше. Пока он не умел перебраться с одной ступеньки на другую, ему не удавалось подняться ни на сантиметр, но едва он научился этому, ему стала доступной не только следующая ступенька, но и вся лестница. Этот эффект мы назовем эффектом лестницы. Схематически он изображен на рис. 5.1.
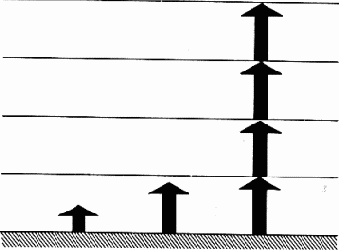
Рис. 5.1. Эффект лестницы
Эффект лестницы лежит в основе многих явлений перехода малых количественных изменений в большие качественные. Возьмем, например, классическую иллюстрацию гегелевского закона перехода количества в качество — кристаллизацию жидкости при опускании температуры ниже точки плавления. Способность молекулы, колеблющейся вблизи определенного положения равновесия, удержать несколько соседних молекул вблизи определенных положений равновесия является как раз «способностью перехода на следующую ступеньку». Когда в результате понижения температуры (уменьшая амплитуды колебаний) такая способность появляется, начинается процесс кристаллизации, и шаг за шагом (ступенька за ступенькой) происходит упорядочивание расположения молекул. Другой известный пример — цепная реакция. Здесь переход на следующую ступеньку — самовоспроизведение реагентов в результате реакции. В физических системах, где все соотношения, важные для поведения системы в целом, имеют статистический характер, эффект лестницы также проявляется статистически; критерий возможности перехода на следующую ступеньку является количественным и статистическим. Эффект лестницы в этом случае можно отождествлять с цепной реакцией, если понимать последний термин в самом полном смысле.
Экспериментальная физика
На рубеже XVI и XVII столетий, когда закладывались основы новой математики, были заложены также основы экспериментальной физики. Ведущая роль принадлежит здесь Галилею (1564–1642), который не только сделал многочисленные открытия, составившие эпоху, но в своих книгах, письмах и беседах учил современников новому методу получения знаний. Воздействие Галилея на умы было огромно. Другим человеком, сыгравшим важную роль в становлении экспериментальной науки, был Френсис Бэкон (1561–1626), выступивший с философским анализом научного знания и метода индукции.
В отличие от древних греков европейские ученые отнюдь не относились с презрением к эмпирическому знанию и практической деятельности. В то же время они полностью овладели теоретическим наследием греков и уже вступили на путь собственных открытий. Сочетание этих аспектов и породило новый метод. Бэкон пишет:
Те, кто занимались науками, были или эмпириками, или догматиками. Первые, подобно муравью, только собирают и пользуются собранным. Вторые, подобно пауку, из самих себя создают ткань. Пчела же избирает средний способ, она извлекает материал из цветов сада и поля, но располагает и изменяет его собственным умением. Не отличается от этого и подлинное дело философии. Ибо она не основывается исключительно или преимущественно на силах ума и не откладывает в сознание нетронутым материал, извлекаемый из естественной истории и из механических опытов, но изменяет его и перерабатывает в разуме. Итак, следует возложить добрую надежду на более тесный и нерушимый (чего до сих пор не было) союз этих способностей опыта и рассудка1.
Этика и эволюция
Но что есть Добро? Что есть Высшее Благо и Высшая Цель? Ответ на эти вопросы, как уже говорилось, выходит за рамки чистого знания, требует волевого акта. Но, может быть, знание подведет нас к какому-то определенному акту, сделает его практически неизбежным?
Давайте подумаем о результатах, к которым приводит следование различным этическим учениям в эволюционирующей Вселенной. Эти результаты в своем главном зависят, очевидно, от того, как соотносятся выдвигаемые учением цели с основным законом эволюции. Основной закон, или план эволюции носит, как и все законы природы, вероятностный характер. Он ничего однозначно не предписывает, но кое-что запрещает. Никто не может действовать вопреки законам природы. Поэтому этические учения, противоречащие плану эволюции, т. е. ставящие цели, несовместимые или даже просто чуждые ему, не могут привести своих последователей к положительному вкладу в эволюцию, а это значит, что они мешают ей и будут вычеркнуты из памяти мира. Таково имманентное свойство развития: то, что соответствует его плану, оно увековечивает в следующих по времени структурах; то, что ему противоречит, преодолевается и гибнет.
Итак, лишь те учения имеют шансы на успех, которые способствуют осуществлению плана эволюции. Если мы рассмотрим под этим углом зрения общепризнанные в настоящее время духовные ценности и принципы общественной жизни, то увидим, что все они самым тесным образом связаны с нашим пониманием плана эволюции, фактически могут быть выведены из него. Это и есть общий знаменатель этических учений, внесших конструктивный вклада историю человечества.
Но между этим объективным и бесстрастным воззрением на этические принципы и решением следовать им — еще большое расстояние. В самом деле, почему это Я должен заботиться о плане эволюции? Какое мне до него дело?
Эволюция мышления
Наша следующая задача в историческом плане — анализ развития мышления начиная с древнейшей фазы, о которой у нас есть надежные сведения. Эта фаза — первобытное общество с культурой позднего палеолита и раннего неолита. Но прежде, чем говорить о первобытном мышлении, прежде, чем «вжиться в роль» первобытного человека, мы исследуем мышление вообще, используя и современный мыслительный аппарат в качестве инструмента исследования, и современное мышление в качестве объекта исследования, непосредственно доступного каждому из нас по личному опыту. Это необходимо, чтобы можно было ясно увидеть отличие первобытного мышления от современного и общее направление развития мышления. Исследование, которое мы собираемся предпринять в двух следующих главах, можно определить как кибернетический подход к основным понятиям логики и к проблеме взаимоотношения языка и мышления.
Как возникает иерархия
Вернемся снова к эволюции нервной системы. Может ли иерархия классификаторов возникнуть эволюционным путем? Очевидно, может, но при одном условии: если создание каждого нового уровня иерархии и его последующего расширения полезны животному в борьбе за жизнь. Из факта существования животных с высокоорганизованной нервной системой мы делаем вывод, что так оно и есть в действительности. Кроме того, изучая примитивных животных, мы видим, что система понятий, которые способна распознавать их нервная система, также весьма примитивна. Следовательно, в пользе нижайшего уровня иерархии классификаторов мы убеждаемся воочию.
Набросаем в общих чертах путь развития нервной системы. На начальных стадиях мы находим у животного всего несколько рецепторов. Число возможных способов связи между ними (соединений) относительно невелико и допускает прямой перебор. По методу проб и ошибок находится выгодное соединение. То, что выгодное соединение может существовать даже при очень малом числе нейронов, легко видеть на таком примере. Пусть есть всего два светочувствительных рецептора. Если они расположены на разных сторонах тела, то информация, которую они дают (разность освещенностей), достаточна, чтобы животное могло двигаться на свет или против света. Когда выгодное соединение найдено и осуществлено, допустим, с помощью одного промежуточного нейрона (такие нейроны называются ассоциативными), вся группа в целом может быть размножена. Так возникает система ассоциативных нейронов, регистрирующих, например, разности между освещенностями рецепторов и суммирующих эти разности (рис. 2.3).
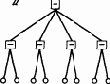
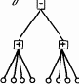
Рис. 2.3. Простейшие типы связей между рецепторами
Может быть размножена также любая часть системы связанных нейронов, например, один или несколько рецепторов. Тогда возникает система связей типа изображенной на рис. 2.3,б. Схемы обоих типов образуют в совокупности первый уровень иерархии, основанный на понятиях суммы и разности освещенностей. Поскольку для корректировки движения животного очень важно регистрировать изменение освещенности в данной точке со временем, можно предположить, что на самых ранних стадиях должны появиться нейроны, срабатывающие при изменении освещенности в точке.
Это может быть как рецептор, так и ассоциативный нейрон, связанный с одним или несколькими рецепторами. В общем виде можно охарактеризовать классификаторы первого уровня как регистрирующие суммы и разности возбуждений рецепторов в пространстве и времени.
Доказав свою полезность для животного, классификаторы первого уровня прочно входят в число его средств борьбы за существование. Тогда начинается следующая серия проб и ошибок: небольшое число классификаторов первого уровня (точнее, их выходных подсистем) связывается между собой в один пробный классификатор второго уровня, пока не получится полезное соединение. Затем оказывается полезным размножение этого соединения. Можно предположить, что на втором уровне иерархии — поскольку это касается органов зрения — появляются такие понятия, как граница между светом и тенью, средняя освещенность пятна, движение границы между светом и тенью и т. п. Таким же путем возникают и следующие уровни иерархии.
Набросанная нами схема наводит на мысль, что любая сложная система, возникшая в процессе эволюции по методу проб и ошибок, должна иметь иерархическую организацию. Действительно, не имея возможности перебрать все мыслимые соединения большого числа элементов, природа перебирает соединения из нескольких элементов, а найдя полезную комбинацию, размножает ее и использует как целое в качестве элемента, который может быть связан с небольшим числом других таких же элементов. Так и возникает иерархия. Это понятие играет огромную роль в кибернетике. Фактически всякая сложная система, как возникшая естественно, так и созданная человеком, может считаться организованной, только если она основана на некой иерархии или переплетении нескольких иерархий. Во всяком случае, до сих пор мы не знаем организованных систем, устроенных иначе.
Как возникает регулирование
Как могла в процессе эволюции возникнуть система, устроенная по схеме регулирования? Мы видим, что возникновение иерархически устроенных классификаторов может быть объяснено как результат совместного действия двух основных факторов эволюции: редупликации биологических структур и нахождения полезных связей по методу проб и ошибок. Не приводит ли действие этих факторов и к появлению схемы регулирования?
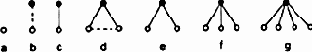
Рис. 2.7. Редупликация рецепторов
Не имея возможности опереться на данные о том реальном эволюционном процессе, который миллионы лет назад породил сложную нервную систему, мы вынуждены удовлетворяться чисто гипотетическим комбинаторным построением, показывающим теоретическую возможность возникновения схемы регулирования. Будем систематически исследовать все возможности, к которым приводят редупликация и отбор. Естественно предположить, что в процессе редупликации сохраняются как связи внутри удвояемой подсистемы, так и связи ее с теми частями, которые не редуплицируются. И еще мы предположим, что между только возникшими подсистемами существует вследствие их близкого расположения связь, которую мы будем изображать штриховой линией и которая может либо укрепиться, либо исчезнуть. Начнем с самого начала, т. е. с того случая, когда мы видим всего одну нервную клетку, являющуюся одновременно и рецептором, и эффектором (рис. 2.7,а). Здесь всего одна возможность редупликации, которая приводит к появлению двух клеток (рис. 2.7,б). Если одна из них оказывается ближе к поверхности, а другая — к мышечным клеткам, то полезно разделение труда между ними. Так возникает схема рецептор — эффектор (рис. 2.7,в). Здесь уже две возможности редупликации. Удвоение рецептора дает схему г на рис. 2.7, которая после исчезновения штриховой связи преобразуется в схему д. Аналогичный процесс порождает схемы е, ж и т. д. Таким образом происходит разрастание нулевого уровня иерархии (рецепторов), о котором говорилось выше.
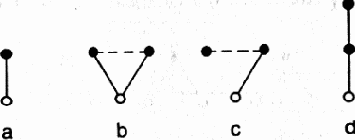
Рис. 2.8. Редупликация эффекторов
На рис. 2.8 показаны схемы, которые возникают из схемы 2.7,в
путем редупликации эффектора.
В схеме б возбуждение одного рецептора должно по двум каналам передаваться двум эффекторам. Однако известно, что электрическое сопротивление синапсов резко падает после того, как по ним первый раз проходит ток. Поэтому если возбуждение направится по одному каналу, то этот канал связи будет закреплен, а второй окажется шунтированным и может «отсохнуть» (схема в). Затем возбуждение может продолжить дорогу через штриховую связь (схема г), что знаменует зарождение первого уровня классификаторов.
На рис. 2.9 представлены возможные варианты развития трехнейронной схемы 2.8,г. Три группы схем соответствуют редупликации различных подсистем исходной системы. Редуплицируемая подсистема обведена кружком. Первая группа (a, б, в) объясняет разрастание нулевого уровня, вторая группа (г, д, е) — первого уровня иерархии классификаторов. В третьей группе (ж, з, и, к) мы видим схемы, возникающие при редупликации одного классификатора первого уровня без связанного с ним рецептора. Переход от схемы з к схеме и объясняется тем «отсыханием» шунтированного канала, которое мы описали выше. Схема к, появившаяся в конечном счете, существенно отличается от всех остальных схем, представлявших иерархии классификаторов. В этой схеме один из классификаторов «повисает в воздухе» — он не получает информации из внешнего мира. Может ли такая схема быть полезной животному? Да: ведь это и есть схема регулирования!
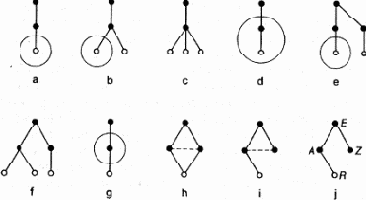
Рис. 2.9. Варианты развития трехнейронной схемы
Мы можем предположить такое, например, воплощение схемы 2.9,к. Рассмотрим некое гипотетическое животное, живущее в морской воде. Пусть R — рецептор, воспринимающий температуру окружающей среды. Вместе с ним регистрирует — путем изменения частоты импульсов возбуждения — температуру воды и классификатор A. Пусть большее или меньшее возбуждение эффектора E вызывает растяжение или сжатие оболочки животного, вследствие чего его объем изменяется, и оно либо поднимается к поверхности моря, либо опускается вглубь. И пусть для нашего животного полезнее всего какая-то определенная температура, скажем 16?.Тогда нейрон Z (фиксатор цели) должен сохранять определенную частоту импульсов, равную той частоте, которую имеет нейрон A при температуре 16?. Эффектор Е должен регистрировать разность возбуждений нейронов A и Z и соответственно с ее знаком поднимать животное к поверхности, где вода теплее, или погружать в более прохладные нижние слои воды. Такое приспособление премного способствовало бы благоденствию измышленного нами животного.
Кибернетический манифест
Валентин Турчин и Клифф Джослин1
1. Философия. Философия отвечает на такие фундаментальные вопросы, как: “Кто я?”, “Откуда я пришел и куда иду?”, “Сколь истинно мое знание?”, “Какова, в конечном счете, природа вещей?”, “Что есть добро и что есть зло?”. Философия важна. Философия является частью нашего знания.
2. Знание. В кибернетической гносеологии знание, принадлежащее кибернетической системе, определяется как некая модель части мира, воспринимаемого этой системой. Модель есть устройство, генерирующее предсказания относительно событий вокруг; эти предсказания используются системой при принятии решений. Понятия смысла и истины следует определять на этой основе.
Знание одновременно субъективно и объективно, ибо оно является результатом взаимодействия субъекта (кибернетической системы) и объекта (среды). Знание об объекте всегда относительно: оно существует только как часть какого-либо субъекта. Мы можем изучать взаимоотношение между знанием и реальностью (прежде всего, истинно или ложно данное знание), тогда субъект знания становится, в свою очередь, объектом для нового субъекта знания. Но знание в любой форме безотносительно какого-либо субъекта есть логическая бессмыслица. Детальное развитие кибернетической гносеологии на основе этих определений крайне важно для формализации естественных наук и философии, а также для интерпретации математических систем.
3. Свобода, воля, управление. В кибернетической метафизике свобода рассматривается как фундаментальное свойство природы. Законы природы суть ограничения на эту свободу, они не обязательно приводят к определенному ходу событий. Понятие свободы подразумевает наличие некоторого активного фактора, который разрешает неопределенность, присущую свободе, выбирая одно определенное действие из множества возможных. Мы называем этот фактор волей. Мы говорим, что воля управляет некоторой кибернетической системой, когда свобода системы ограничивается действиями, выбираемыми волей.
4. Метасистемный переход. Когда некоторое число систем интегрируются в единое целое с возникновением нового уровня управления, мы говорим, что имеет место метасистемный переход.
Новая система есть метасистема по отношению к старым. Метасистемный переход является по определению творческим актом. Он не может совершиться под воздействием одних лишь внутренних факторов интегрируемой системы, но всегда требует вмешательства извне, “сверху”.
5. Эволюция. Метасистемный переход — квант эволюции. Высокоорганизованные системы, включая живые существа, суть многоуровневые иерархии по управлению, возникающие в результате метасистемных переходов разного масштаба. Главнейшие эволюционные сдвиги — это крупномасштабные метасистемные переходы, происходящие в рамках естественного отбора как проявления общего принципа проб и ошибок. Примеры: формирование редуплицирующихся макромолекул, образование многоклеточных организмов, появление разума, образование человеческого общества.
6. Человеческий разум. Человеческий разум, как нечто новое по сравнению с разумом животных, возникает в результате метасистемного перехода: мозг получает возможность управлять формированием ассоциаций ментальных представлений. Все специфические черты человеческого разума, включая воображение, самосознание, преодоление инстинктов, постановку целей, юмор, чувство прекрасного, могут быть объяснены как результат этого метасистемного перехода.
7. Социальная интеграция. Возникновение человеческого разума тесно связано со следующим, в настоящее время протекающим метасистемным переходом, а именно: интеграцией человеческих существ в человеческое общество. Человеческое общество качественно отличается от сообществ животных благодаря способности людей создавать и развивать (а не только использовать для передачи сообщений) язык. Язык выполняет две функции: обмен информацией между индивидуумами и создание моделей действительности. Эти две функции на уровне социальной интеграции аналогичны функциям нервной системы на уровне интеграции клеток в многоклеточный организм. В материале языка люди создают новые символьные модели действительности (в частности, научные теории), которых не было создано природой на уровне нашей нервной системы.
Язык — это как бы продолжение человеческого мозга. Более того, это единое продолжение мозга всех членов общества. Это коллективная модель действительности, которая совершенствуется всеми членами общества и передается от поколения к поколению. Давно отмечено, что человеческое общество можно рассматривать как единый организм. Тело этого организма есть совокупность всех людей и ими сделанных вещей. Его “физиология” — это культура общества и, прежде всего, язык.
8. Эра разума. Возникновение человеческого общества знаменует начало новой эры Универсальной Эволюции. Если раньше единственным механизмом эволюции был естественный отбор на базе мутаций генофонда, то теперь мы видим несравненно более быстрый процесс: эволюцию культуры человеческого общества. Вариация и селекция по методу проб и ошибок происходят теперь как результат сознательной воли человека. Двигателем эволюции мироздания становится творческая человеческая личность. Эволюция культуры, прогресс науки и техники перехватывают инициативу у биологической эволюции.
9. Глобальная интеграция. Пытаясь заглянуть в будущее, мы предсказываем, что социальная интеграция будет продолжаться в двух направлениях, которые можно назвать шириной и глубиной. С одной стороны, интеграция мировых культур приведет к образованию единого мирового сообщества и мирового правительства с ответственностью за экологию Земного шара. Этика кибернетического мировоззрения требует, чтобы каждый из нас заботился о сохранении вида и экосистемы и о максимизации потенциала для следующих шагов эволюции и интеграции.
10. Человеческие сверхсущества. С другой стороны, мы предвидим продолжение интеграции “в глубину”, а именно: физическую интеграцию индивидуальных нервных систем с созданием потенциально бессмертных человеческих сверхсуществ. Опираясь на известный эволюционно-биологический принцип: онтогенез повторяет филогенез, мы можем предположить, что человеческие индивидуумы будут рождаться и жить в молодом и зрелом возрасте подобно тому, как они живут сейчас, а затем принимать или отвергать интеграцию в сверхсущество.
Таким образом, физическая интеграция индивидуумов приходит не на смену индивидуальной жизни, как мы ее знаем сейчас, а в дополнение к ней.
11. Высшие человеческие ценности. Представление о бессмертии есть часть проблемы высших человеческих ценностей. Поведение кибернетических систем, каковыми являются живые существа, определяется некоторыми целями. Эти цели образуют иерархию: чтобы достичь цели более высокого уровня, система должна поставить и достичь ряд целей более низкого уровня. Иерархия целей существа имеет вершину: наивысшие цели или ценности. У животного высшие цели врожденные — это инстинкты выживания и размножения. У человека высшие ценности могут идти дальше инстинктов и даже противоречить им. Как и всякий элемент культуры, представление о высших ценностях жизни внушается человеку обществом, в котором он живет. Однако, в конечном счете, человек сам устанавливает для себя высшие ценности, совершая акт свободного выбора. В результате мы имеем множество этических и религиозных учений. Однако у большинства таких учений мы находим общий знаменатель: ту или иную форму воли к бессмертию. Животное не осознает неизбежности своей смерти; человек осознает. Воля человека к бессмертию является естественным продолжением воли к жизни.
12. Упадок метафизической веры в бессмертие. В традиционных религиях, как, например, христианстве, мы находим представление о бессмертии, которое можно назвать метафизическим. Это представление о бессмертии души и загробной жизни. Протест против смерти используется здесь как стимул для принятия учения; ведь оно с самого начала обещает бессмертие. Однако под влиянием критического научного метода метафизическое представление о бессмертии, некогда конкретное и притягательное, становится все более абстрактным и бледным. Традиционные религиозные системы медленно, но верно теряют влияние.
13. Творческое бессмертие. Другой род бессмертия может быть назван творческим или эволюционным. Это представление о том, что смертное человеческое существо достигает бессмертия, внося свой вклад в некий универсальный бесконечный процесс, который разные люди называют по-разному (История, Культура), а мы называем Эволюция.
Вера в эту форму бессмертия лежит, по-видимому, в основе представления о смысле жизни у большинства творческих людей.
14. Кибернетическое бессмертие. Успехи науки позволяют поднять знамя кибернетического бессмертия. Человеческое существо есть, в конечном счете, кибернетическая система — определенная форма организации материи, которая включает многоуровневую иерархию управления. То, что мы называем нашей душой или сознанием, ассоциируется с высшим уровнем в этой иерархии. Наша организация постоянно переживает частичную смену материала, в котором она выполнена. Не видно причин, по которым эта смена не могла бы идти сколь угодно далеко, включая переход к совершенно новым материалам и к принципиально неограниченному времени существования.
15. Бессмертие и эволюция. Кибернетическая интеграция должна сохранить творческое ядро человеческой личности, ибо оно является двигателем эволюции. Она также должна сделать личность бессмертной, ибо с эволюционной точки зрения нет смысла обрывать ее существование. В биологической эволюции источником вариаций являются мутации генов. Природа творит, экспериментируя на генотипах и отбирая по фенотипам. Поэтому она уничтожает старые фенотипы, т. е. биологические тела, чтобы продолжать экспериментирование, эволюцию. Смертность многоклеточных организмов эволюционно необходима. В эру разума, когда ведущей ветвью эволюции является эволюция человеческого общества, источником эволюции становится человеческий мозг. Он не объект, а субъект экспериментирования, его потеря при умирании есть эволюционная нелепость. Личность должна быть бессмертной, как бессмертны гены. Бессмертие человеческой личности стоит на повестке дня Космической Эволюции.
16. Эволюция человеческой личности. Бессмертие человеческой личности не означает ее застывшей неизменности. Это может быть понято по аналогии с организацией на уровне макромолекул. Контролеры биологической эволюции — это гены, и они бессмертны. Однако они не остаются неизменными, а непрерывно изменяются вследствие мутаций, так что хромосомы человека, например, весьма и весьма отличаются от примитивных хромосом вирусов.
Кибернетически бессмертные личности могут меняться и развиваться во взаимодействии с другими личностями сверхсущества, а также при взаимодействии между сверхсуществами, ибо плюрализм необходим для эволюции, и человечество, надо надеяться, будет пробовать различные виды интеграции, создавая различные сверхсущества. Те человеческие личности, которые возникнут в результате всех этих процессов, будут, вероятно, отличаться от нас так, как наши хромосомы отличаются от вирусов. Но определяющий принцип личности останется, по-видимому, неизменным, как остался неизменным принцип работы генов.
17. Как может происходить интеграция. Следует ли ожидать, что все человечество объединится в единое сверхсущество? С эволюционной точки зрения это и нежелательно, и маловероятно. Жизнь можно сравнить с пирамидой: вершина поднимается ввысь и одновременно расширяется основание. Хотя человечество и осуществляет контроль над биосферой, наши тела составляют лишь небольшую часть от всей биомассы. Основную ее часть все еще составляют примитивные организмы, такие, как мы находим в планктоне. Осуществление кибернетического бессмертия потребует, несомненно, чем-то пожертвовать; для начала, надо будет решительно сосредоточить усилия на дальнейшем развитии науки. Совсем не очевидно, что большинство людей в большинстве сообществ захотят поставить перед собой такую цель. Воля к бессмертию, как и всякая человеческая черта, широко варьируется от человека к человеку. Поскольку интеграция может быть лишь добровольной, надо ожидать, что только часть, вероятно небольшая, человечества образует сверхсущества, большинство же останется в состоянии “человеческого планктона”.
18. Интеграция на Космической сцене. Однако именно интегрированному человечеству суждено освоить Космическое пространство. Неинтегрированная часть не может конкурировать с нею; она может лишь поставлять материал для сверхсуществ. Без интеграции человечество не может претендовать на какую-либо серьезную роль в Космосе. Системные единицы, которые принимают решения, должны получать вознаграждение за свои решения; иначе они никогда не примут их.
Попробуйте представить себе картину “человеческого планктона”, набитого в ракеты, чтобы достичь отдаленной звезды через десять или двадцать поколений. Играть роль в Космосе могут лишь существа, продолжительность жизни которых исчисляется Космическими же временами.
19. Сегодняшние проблемы. Наше представление о кибернетической интеграции в настоящее время весьма абстрактно и туманно. Это неизбежно: понятия и цели, касающиеся отдаленного будущего, только и могут быть абстрактными. Это не значит, однако, что они не имеют никакого отношения к нашим сегодняшним проблемам. Понятия о Всемирной Эволюции и кибернетическом бессмертии имеют прямое отношение к понятию о смысле жизни и к высшим ценностям, которые мы принимаем для себя сегодня, хотя те, кто живут сейчас, могут реалистически думать лишь в терминах творческого бессмертия (хотя, кто знает?). Проблема высших ценностей — это центральная проблема нынешнего общества. Ради чего надо жить, после того как наши основные потребности с легкостью удовлетворены современной системой производства? Что есть Добро и что есть Зло? Каковы те конечные критерии, на основании которых мы должны оценивать различные модели общественного устройства? В истории человечества великие цивилизации неотделимы от великих религий, которые отвечали на эти вопросы. Упадок традиционных религий, основывающихся на метафизическом понятии о бессмертии, угрожает деградацией общества. Представление о кибернетическом бессмертии может прийти на смену своему метафизическому предшественнику и послужить основой для учения о высших ценностях нарождающейся глобальной цивилизации.
20. Интеграция и свобода. В наше время мы можем яснее, чем когда-либо, видеть фундаментальное противоречие конструктивной эволюции человеческого общества: между социальной интеграцией и личной свободой. Интеграция есть эволюционная необходимость; это очередной метасистемный переход. Если человечество поставит себе цели, не совместимые с интеграцией, результатом будет эволюционный тупик.
Тогда мы не выживем. В эволюционирующей Вселенной нет остановки: все, что не развивается, гибнет. С другой стороны, драгоценной сущностью человека является свобода. Творческая свобода личности — это двигатель эволюции в эпоху разума. Если она будет подавлена интеграцией, как в тоталитарных режимах, мы тоже окажемся в эволюционном тупике.
Это противоречие реально, но ниоткуда не следует, что оно неразрешимо. В конце концов, аналогичное противоречие успешно преодолевалось эволюцией на предыдущих уровнях организации. Когда клетки объединяются в многоклеточный организм, они продолжают выполнять свои биологические функции — обмен веществ и деление. Новое качество — жизнь организма — появляется не вопреки биологическим функциям индивидуальных клеток, а благодаря им. Творческий акт свободной человеческой личности — это его “биологическая функция”. В интегрированном сверхсуществе на всех его стадиях, начиная с той, которая протекает сейчас, эта свобода должна оставаться необходимым и решающим фактором. Как достичь органического синтеза интеграции и свободы — вот вызов, который природа бросает человеку.
1
Turchin V., Joslyn С. // Kybernetes. 1991, Vol. 19, N 2, 3. Перевод с небольшими вариациями В.Турчина.
+++
Кибернетика
Анализ эволюции в кибернетический период, вскрытие законов, по которым происходит усложнение организации живых существ этого периода — мы будем для краткости называть их «кибернетическими животными», — требует введения некоторых фундаментальных понятий и законов кибернетики.
Сам термин «кибернетика« ввел, как известно, Норберт Винер, определив его описательно как учение о связях и управлении в живом организме и машине. Чтобы более точно дать определение кибернетики, как и всякой научной дисциплины, мы должны ввести ее основные понятия. Собственно говоря, ввести основные понятия — это и значит уже определить данную науку, ибо остается только добавить: описание мира с помощью этой вот системы понятий и есть данная конкретная наука.
В основе кибернетики лежит прежде всего понятие системы как некоторого материального объекта, состоящего из других объектов, называемых подсистемами данной системы. Подсистема некоторой системы, в свою очередь, может рассматриваться как система, состоящая из подсистем. Поэтому, если быть точным, смысл введенного нами понятия заключается не в термине «система» самом по себе, т. е. не в приписывании некоторому объекту свойства «быть системой», что довольно бессодержательно, ибо каждый объект может считаться системой, а в связи между терминами «система» и «подсистема», отражающей определенное отношение объектов.
Второе важнейшее понятие кибернетики — понятие состояния системы (подсистемы). Подобно тому как понятие системы непосредственно опирается на нашу пространственную интуицию, понятие состояния непосредственно опирается на нашу интуицию времени, и его невозможно определить иначе, как сославшись на опыт. Когда мы видим, что объект в чем-то изменился, мы говорим, что он перешел в другое состояние. Как и понятие системы, понятие состояния является скрытым отношением — отношением между двумя моментами времени. Если бы мир был неподвижным, понятие состояния не могло бы возникнуть, и в тех дисциплинах, где мир рассматривается статически, например, в геометрии, понятие состояния отсутствует.
Кибернетика изучает организацию систем в пространстве и времени, т. е. то, каким образом связаны подсистемы в систему и как влияет изменение состояния одних подсистем на состояние других подсистем. Основной упор делается, конечно, на организацию во времени, которая в случае, когда она целенаправленна, называется управлением. Причины связи между состояниями системы и вытекающие отсюда особенности ее поведения во времени часто называют заимствованным из физики термином динамика системы. Этот термин в применении к кибернетике неудачен, так как, говоря о динамике системы, мы склонны рассматривать ее как нечто целое, в то время как в кибернетике главным является исследование воздействия друг на друга подсистем, образующих данную систему. Поэтому мы предпочитаем говорить об организации во времени, употребляя термин динамическое описание только тогда, когда его нужно противопоставить статическому описанию, учитывающему лишь пространственные отношения между подсистемами.
Кибернетическое описание может иметь различный уровень детализации. Одну и ту же систему можно описывать либо в общих чертах, разбив ее на несколько крупных подсистем, «блоков», либо более детально, описав строение и внутренние связи каждого блока. Но так или иначе кибернетическое описание всегда имеет какой-то конечный уровень, глубже которого оно не распространяется. Подсистемы этого уровня рассматриваются как элементарные, не разложимые на составные части. Реальная физическая природа элементарных подсистем кибернетика не интересует, ему важно только, как они связаны между собой. Два физических объекта могут радикально отличаться друг от друга по своей природе, но если на каком-то уровне кибернетического описания они организованы из подсистем одинаково (с учетом динамического аспекта!), то с точки зрения кибернетики их можно считать — на данном уровне описания — тождественными. Поэтому одни и те же кибернетические соображения могут быть применимы к таким разным объектам, как радиотехническая схема, программа для вычислительной машины или нервная система животного.
Классический период
Итак, несколько дополнительных точек и линий на чертеже, цепочка логических рассуждений — и в результате из простых и очевидных истин мы получаем истины далеко не простые и далеко не очевидные, в справедливости которых, однако, никто не может ни на минуту усомниться. Это стоит того, чтобы принести в жертву богам быка! Можно представить себе восторг, который испытали греки, совершив такое открытие. Они напали на золотую жилу и с усердием принялись ее разрабатывать. Уже во времена Пифагора (550 г. до н. э.) занятия математикой были очень распространены среди людей, обладавших досугом, и считались делом благородным, почетным и даже священным. Достижения и открытия, одно другого чудеснее, посыпались как из рога изобилия.
Возникновение доказательства — это метасистемный переход в рамках языка. Формула перестает быть вершиной языковой деятельности, появляется новый класс языковых объектов — доказательства и новый вид языковой деятельности, направленный на исследование и производство формул. Это новый этаж иерархии по управлению, и его появление вызывает огромный рост числа формул (закон разрастания предпоследнего уровня).
Метасистемный переход всегда означает качественный скачок, взлет на новую ступень, бурное взрывоподобное развитие. Математика стран Древнего Востока оставалась почти неизменной на протяжении одного-двух тысячелетий, и наш современник читает о ней со снисхождением взрослого к ребенку. Греки же за одно-два столетия создали всю геометрию, над изучением которой трудятся в поте лица наши старшеклассники. И даже больше, ибо школьная программа по геометрии охватывает лишь часть достижений культуры (до 330 г. до н. э.). Вот краткая летопись математики классического периода.
585 г. до н. э. Фалес Милетский. Первые геометрические теоремы.
550 г. до н. э. Пифагор и его последователи. Теория чисел. Учение о гармонии. Построение правильных многогранников. Теорема Пифагора. Открытие несоизмеримых отрезков. Геометрическая алгебра. Геометрические построения, эквивалентные решению квадратных уравнений.
500 г. до н. э. Гиппас-пифагореец, который должен был порвать со своими товарищами, так как делился с посторонними людьми своими знаниями и открытиями (у пифагорейцев это запрещалось). Он дал, в частности, построение шара, описанного вокруг додекаэдра.
430 г. до н. э. Гиппократ Хиосский (не путать с врачом Гиппократом из Коса). Считался самым знаменитым геометром V в. до н. э. Занимался квадратурой круга, осуществляя сложные геометрические построения. Ему известна связь между вписанными углами и дугами, построение правильного шестиугольника, обобщение теоремы Пифагора для тупоугольных и остроугольных треугольников. Все это для него, видимо, уже азбучные истины. Он может квадрировать любой многоугольник, т. е. построить для него квадрат равной площади.
427–348гг. до н. э. Платон. Он сам хотя и не получал новых математических результатов, но математику знал, и она играла важную роль в его философии точно так же, как философия Платона сыграла важную роль в математике. Крупнейшие математики своего времени: Архит, Теэтет, Евдокс и другие были друзьями Платона, его учениками в области философии и учителями в области математики.
390 г. до н. э. Архит Тарентский. Стереометрическое решение задачи об удвоении куба, т. е. построение куба с объемом, равным удвоенному объему данного куба.
370 г. до н. э. Евдокс Книдский. Изящная, логически безукоризненная теория пропорций, вплотную подходящая к современной теории действительного числа. «Метод исчерпывания», лежащий в основе современного понятия об интеграле.
384–322 гг. до н. э. Аристотель. Он положил начало логике и физике. Труды Аристотеля обнаруживают полное владение математическим методом и знание математики, хотя он, подобно своему учителю Платону, и не сделал в ней никаких открытий. Аристотель-философ немыслим без Аристотеля-математика.
300 г. до н. э. Евклид. Он живет уже в новую Александрийскую эпоху. В своих знаменитых «Началах» Евклид собрал и систематизировал все важнейшие труды по математике, существовавшие в конце IV в.до н. э., и изложил их в том же духе, как это было принято в школе Платона. В течение более чем двух тысячелетий школьные курсы геометрии следуют, с большей или меньшей степенью точности, «Началам» Евклида.
Кое-что о реальных иерархиях
До сих пор наши выводы были чисто умозрительны. Как они подтверждаются реальным строением нервной системы животных и что можно сказать о понятиях промежуточных уровней иерархии, реально складывающейся в процессе эволюции?
При сравнении нашей схемы с действительностью необходимо учитывать следующее.
Деление системы понятий на уровни не является столь безусловным, как мы молчаливо предполагали. Могут быть случаи, когда понятия k-го уровня непосредственно используются на k+2-м уровне, минуя k+1-й. На рис. 2.2 мы втиснули такую возможность в общую схему, введя классификаторы, связанные лишь с одним классификатором предыдущего уровня и повторяющие его состояния; они изображены перечеркнутыми квадратиками. В действительности, конечно, их нет, что затрудняет расчленение системы на уровни. Далее, иерархия классификаторов, изображенная на рис. 2.2, имеет четко выраженный пирамидальный характер: чем выше уровень, тем меньше классификаторов, а на верхнем уровне он всего один. Такая ситуация имеет место, когда система чрезвычайно «целенаправленна», т. е. служит для какой-то весьма узкой цели, для какого-то четко определенного способа классификации ситуаций. В примере, который мы приводили, это было распознавание «домиков». И мы видели, что уже неправильные трех- или четырехугольники для такой системы оказываются «бессмысленными»; они не вписываются в иерархию понятий. Чтобы быть более универсальной, система должна быть подобной не одной пирамиде, а многим пирамидам, вершины которых расположены приблизительно на одном уровне и образуют множество понятий (а точнее, множество систем понятий), в терминах которых происходит управление действиями животного и которые обычно обнаруживаются при исследовании его поведения. Об этих понятиях говорят, что они составляют основу определенного «образа» внешнего мира, который складывается в представлении животного (или человека). Состояние классификаторов этого уровня является непосредственной информацией для исполнительной части нервной сети (т.
е. в конечном счете для эффекторов). Каждый из этих классификаторов опирается на определенную иерархию классификаторов — пирамиду, по которой движется информация так, как это было описано выше. Однако пирамиды могут перекрываться в своих средних частях (и заведомо перекрываются в своей нижней части — рецепторах). Общее число вершин пирамиды может быть теоретически как угодно велико, в частности, оно может быть много больше общего числа рецепторов. Это тот случай, когда одна и та же информация, доставляемая рецепторами, представляется множеством пирамид в множестве различных форм, рассчитанных на все случаи жизни.
Отметим еще одно обстоятельство, которое следует учитывать при поисках иерархии в реальной нервной сети. Если мы видим нейрон, соединенный синапсами с сотней рецепторов, то это еще не значит, что он фиксирует какое-то простое понятие первого уровня типа суммарного числа возбуждений рецепторов. Логическая функция, связывающая состояние нейрона с состоянием рецепторов, может быть весьма сложной и имеющей собственную иерархическую структуру.
Концепция Сепира-Уорфа
Очень интересны с этой точки зрения работы двух американских лингвистов — Э.Сепира и Б.Уорфа. О воззрениях Сепира дает представление следующая цитата, взятая в качестве эпиграфа Б.Уорфом к его статье «Отношение норм поведения и мышления к языку»1:
Люди живут не только в объективном мире вещей и не только в мире общественной деятельности, как это обычно полагают; они в значительной мере находятся под влиянием того конкретного языка, который является средством общения для данного общества. Было бы ошибочным полагать, что мы можем полностью осознать действительность, не прибегая к помощи языка, или что язык является побочным средством разрешения некоторых частных проблем общения и мышления. На самом же деле «реальный мир» в значительной степени бессознательно строится на основе языковых норм данной группы... Мы видим, слышим и воспринимаем так или иначе те или иные явления главным образом благодаря тому, что языковые нормы нашего общества предлагают данную форму выражения.
Б.Уорф, принимая за основу эту концепцию, конкретизирует ее в своих исследованиях некоторых индейских языков и культур и их сравнении с европейскими языками и культурой. Мы изложим некоторые наблюдения и мысли Уорфа о таких логических категориях, как пространство и время, форма и содержание2.
Уорф замечает, что для правильной оценки значений таких категорий необходимо, прежде всего, отрешиться от тех воззрений на взаимоотношения языка и мышления, которые обычно считаются неотъемлемой частью «здравого смысла» и которые Уорф называет естественной логикой. Он пишет:
Естественная логика утверждает, что речь — это лишь внешний процесс, связанный только с сообщением мыслей, но не с их формированием. Считается, что речь, т. е. использование языка, лишь «выражает» то, что уже в основных чертах сложилось без помощи языка. Формирование мысли — это якобы самостоятельный процесс, называемый мышлением или мыслью и никак не связанный с природой отдельных конкретных языков. Грамматика языка — это лишь совокупность общепринятых традиционных правил, но использование языка подчиняется якобы не столько им, сколько правильному, рациональному или логическому мышлению.
Мысль, согласно этой системе взглядов, зависит не от грамматики, а от законов логики и мышления, будто бы одинаковых для всех обитателей Вселенной и отражающих рациональное начало, которое может быть обнаружено всеми разумными людьми независимо друг от друга, безразлично, говорят ли они на китайском языке или на языке чоктав. У нас принято считать, что математические формулы и постулаты формальной логики имеют дело как раз с подобными явлениями, т. е. со сферой и законами чистого мышления. Естественная логика утверждает, что различные языки — это в основном параллельные способы выражения одного и того же понятийного содержания, что поэтому они различаются лишь незначительными деталями, которые только кажутся важными. По этой теории — математика, символическая логика, философия и т. п. — это не особые ответвления языка, но системы, противостоящие языку и имеющие дело непосредственно с областью чистого мышления.
Эта концепция укоренилась так глубоко, что мы даже не осознаем, что она может быть подвергнута критическому анализу. Так, мы осознаем, что дышим воздухом, только когда его нам начинает не хватать. Уорф приводит еще одну иллюстрацию. Предположим, что какой-то народ вследствие определенного дефекта зрения способен воспринимать только синий цвет. В таком случае его люди вряд ли смогут сформулировать ту мысль, что они видят лишь синий цвет. Сам термин синий будет лишен для них того смысла, который вкладываем в него мы, противопоставляя его красному, желтому и т. д. Подобно этому подавляющее большинство людей, говоря или, во всяком случае, думая на одном языке, просто лишены возможности осознать те ограничения, которые он накладывает, и тот элемент произвола, который он содержит. Они лишены возможности сравнения, поэтому ограничения и произвол родного языка кажутся им чем-то универсальным и безусловным, лежащим в самой природе вещей. Когда лингвисты критически исследовали много языков, весьма различающихся по своему строю, они столкнулись с нарушением тех закономерностей, которые ранее считались универсальными.
Оказалось, что грамматика — не просто инструмент для воспроизведения мысли, но программа и руководство мыслительной деятельности индивидуума. Уорф пишет:
Мы расчленяем природу в направлении, подсказанном нашим родным языком. Мы выделяем в мире явлений те или иные категории и типы совсем не потому, что они (эти категории и типы) самоочевидны; например, мир предстает перед нами как калейдоскопический поток впечатлений, который должен быть организован нашим сознанием, а это значит в основном — языковой системой, хранящейся в нашем сознании.
Здесь следует заметить, что в последней части приведенной цитаты, где говорится об организации потока впечатлений, Уорф явно увлекается и неверно описывает разделение труда между нейронной и языковой системами, приписывая организацию впечатлений «в основном» языковой системе. В действительности, конечно, огромная часть работы по первичной организации впечатлений выполняется на нейронном уровне, и язык получает уже не сырье, а совершенно определенным способом обработанный полуфабрикат. Здесь Уорф совершает ту же самую ошибку по отношению к нейронной системе, которую, как он справедливо указывает, совершает «естественная логика» по отношению к языковой системе. Он недооценивает нейронную систему из-за того, что она одинакова у всех людей и никакой другой нейронной системы мы не знаем.
К выводу о важности языковой системы для организации впечатлений трудно прийти, если ограничиться сравнением лишь современных европейских языков да еще, возможно, латинского и древнегреческого. Системы этих языков в своих существенных чертах совпадают, что служит аргументом в пользу концепции естественной логики. Но это совпадение объясняется только тем, что европейские языки (за небольшим исключением) принадлежат к одной семье индоевропейских языков, построены в основном по одному и тому же плану и имеют общий исторический корень. Кроме того, они в течение долгого времени участвовали в создании общей культуры и культура эта во многом, и особенно в интеллектуальной области, развилась под определяющим влиянием двух индоевропейских языков: греческого и латыни.Чтобы определить ширину диапазона возможных грамматик, надо обратиться к более экзотическому языковому материалу. Для Уорфа таким материалом служат языки американских индейцев: хопи, шауни и др. По сравнению с ними европейские языки так близки друг к другу, что Уорф объединяет их для удобства сопоставления в один «среднеевропейский стандарт» языка.
Консерватизм докритического мышления
Докритическому мышлению внутренне присущ консерватизм, он является непосредственным следствием отсутствия аппарата изменения языковых моделей. Всевозможные регламентации и запреты направляют поступки и мышление по строго определенному пути, освященному традицией. Нарушение традиций вызывает суеверный ужас. Известны случаи, когда люди, случайно нарушившие табу, умирали, когда узнавали об этом. Они знали, что должны умереть и умирали в результате самовнушения.
Это не значит, конечно, что в первобытном обществе вообще не происходит прогресса. В рамках дозволенного обычаем первобытные люди проявляют порой чудеса искусства, ловкости, терпения, настойчивости. В тех же рамках из поколения в поколение совершенствуются орудия и оружие, накапливается опыт. Но вот беда — рамки эти чрезвычайно узки и жестки. Только крайние обстоятельства могут заставить племя (а, скорее всего остатки племени, уничтоженного врагами или умирающего от голода) нарушить обычай. Вероятно, именно в таких ситуациях совершались крупнейшие сдвиги в первобытной культуре. Народ, попавший в изоляцию и из-за не слишком благоприятных природных условий не имеющий возможности расплодиться и распасться на смертельно враждующие народы, может в течение тысячелетий сохранять неизменный уровень первобытной культуры.
На стадии докритического мышления язык играет парадоксальную роль. Выполняя свою коммуникативную функцию — общение между людьми, передача опыта от поколения к поколению, стабилизация социальных групп, он служит на пользу людям. Но вот его некоммуникативная, моделирующая функция приносит больше вреда, чем пользы. Мы имеем в виду те модели, которые создаются не на уровне ассоциации неязыковых представлений, а только на уровне языка, т. е. главным образом первобытную «теорию духов». Как мы уже отмечали, коммуникативная функция и становится-то возможной лишь благодаря моделирующей функции. Но пока языковые модели лишь отражают нейронные модели, мы говорим о чистой коммуникативной функции, когда же создаются новые модели — теории, мы говорим о функции некоммуникативной.
В первобытном обществе мы видим две теории: зачатки арифметики (счет с помощью пальцев, зарубок и т. п.) и «теорию духов». Арифметика, конечно, явление положительное, но она не играет большой роли в жизни первобытного человека, у многих народов она практически отсутствует; напротив, «теория духов» пронизывает всю его жизнь и оказывает на нее отрицательное влияние. В этом и состоит парадокс; первые самостоятельные шаги языковой системы, которые по идее должны привести (в дальнейшем действительно приводят) к огромному скачку в моделировании действительности, на первых порах дают ядовитые выделения, тормозящие дальнейшее развитие. Это результат дикого, так сказать, произрастания «теории духов». Ее можно сравнить с сорняком, вырастающим на хорошо удобренной почве, если не следить за огородом. Семена сорняков, как мы видели, содержатся в самой почве — языке. Только переход на уровень критического мышления — тщательная культивация почвы, селекция культурных растений и борьба с сорняками — дает ожидаемый урожай.