Критерии выбора теорий
Прежде всего, заметим, что ясное осознание научных теорий как языковых моделей действительности значительно снижает остроту конкуренции между научными теориями по сравнению с наивной точкой зрения (родственной платонизму), согласно которой языковые объекты теории лишь выражают какую-то реальность и поэтому каждая теория либо «на самом деле» истинна, если эта реальность «на самом деле» существует, либо «на самом деле» ложна, если эта реальность вымышленная. Эта точка зрения порождена перенесением положения, которое имеет место для языка конкретных фактов, на язык понятий-конструктов. Когда мы сравниваем два конкурирующих утверждения: «в этом стакане — чистый спирт» и «в этом стакане — чистая вода», мы знаем, что эти утверждения допускают опытную проверку и то из них, которое не подтвердилось, теряет всякий модельный смысл, всякую долю истинности; оно на самом деле ложное и только ложное. Совсем иначе обстоит дело с утверждениями, выражающими общие принципы научных теорий. Из них выводится множество проверяемых следствий, и если некоторые из них оказываются ложными, то обычно говорят, что к данной сфере опыта исходные принципы (или способы вывода следствий) неприменимы; обычно удается установить и формальные критерии применимости. Поэтому общие принципы в некотором смысле «всегда истинны», точное понятие истинности и ложности неприменимы к ним, а применимо лишь понятие о большей или меньшей их полезности для описания действительных фактов. Подобно аксиомам математики, общие принципы физики — это абстрактные формы, в которые мы стремимся втиснуть природные явления. Конкурирующие принципы отличаются тем, насколько хорошо они это позволяют сделать.
Но что значит хорошо?
Если теория — это модель действительности, то, очевидно, она тем лучше, чем шире область ее применимости и чем больше предсказаний она может сделать. Это и есть первый критерий для сравнения теорий — критерий общности и предсказательной силы теории.
Далее, поскольку теории — это модели, рассчитанные на использование людьми, они, очевидно, тем лучше, чем проще в употреблении.
Это второй критерий — критерий простоты теории.
Эти критерии довольно очевидны. Если рассматривать научные теории как нечто стабильное, не подверженное развитию и улучшению, то, пожалуй, трудно было бы выдвинуть в дополнение к этим критериям какие-либо еще. Но человечество непрерывно развивает и улучшает свои теории и это порождает еще один критерий — динамический, который и оказывается решающим. Об этом критерии хорошо сказано Филиппом Франком в книге «Философия науки», и мы приведем его слова.
Если мы посмотрим, какие теории действительно предпочитались из-за их простоты, то найдем, что решающим основанием для признания той или иной теории было не экономическое и не эстетическое, а скорее то, которое часто называлось динамическим. Это значит, что предпочиталась та теория, которая делала науку более динамичной, т. е. более пригодной для экспансии в область неизвестного. Это можно уяснить с помощью примера, к которому мы часто обращались в этой книге: борьба между коперниковской и птолемеевской системами. В период между Коперником и Ньютоном очень много оснований приводилось в пользу как одной, так и другой системы. В конце концов, однако, Ньютон выдвинул теорию движения, которая блестяще объясняла все движения небесных тел (например, комет), в то время как Коперник, так же как и Птолемей, объяснял только движения в нашей планетной системе... Однако законы Ньютона основывались на обобщении коперниковской теории, и мы вряд ли можем представить себе, как они могли бы быть сформулированы, если бы он исходил из птолемеевской системы. В этом, как и во многих других отношениях, теория Коперника была более «динамичной», т. е. имела большее эвристическое значение. Можно сказать, что теория Коперника была математически более «простой» и более динамичной, чем теория Птолемея4.
Эстетический критерий, или критерий красоты теории, о котором упоминает Франк, трудно защищать как самостоятельный, независимый от других критериев. Однако он приобретает большое значение как интуитивный синтез всех указанных критериев.Теория представляется ученому красивой, если она достаточно обща и проста и он предчувствует, что она окажется динамичной. Конечно, он может при этом и ошибиться.
Крушение детерминизма
Второй важный результат квантовой механики, имеющий общефилософское значение, — это крушение детерминизма. Детерминизм — это понятие философское. Этим именем называют воззрение, согласно которому все события, происходящие в мире, имеют вполне определенные причины и происходят с необходимостью, т. е. не произойти не могут. Попытки уточнить это определение обнаруживают в нем логические дефекты, которые мешают точной формулировке этого воззрения в виде научного положения без введения каких-либо дополнительных представлений об объективной реальности. В самом деле, что значит «события имеют причины»? Разве можно указать какое-то «конечное» число причин данного события и сказать, что других причин нет? И что значит, что событие «не могло не произойти»? Если только то, что оно произошло, то утверждение обращается в тавтологию.
Однако философский детерминизм может получить более точное истолкование в рамках научной теории, претендующей на универсальное описание реальности. И действительно, он получил такое истолкование в рамках механицизма — научно-философской концепции, возникшей на базе успехов классической механики в приложении к движениям небесных тел. Согласно механистической концепции мир — это трехмерное евклидово пространство, заполненное множеством элементарных частиц, которые движутся по некоторым траекториям. Между частицами действуют силы, зависящие от их расположения друг относительно друга, а движение частиц подчиняется законам механики Ньютона. При таком представлении о мире его точное состояние (т. е. координаты и скорости всех частиц) в некоторый фиксированный момент времени однозначно определяет точное состояние мира в любой другой момент. Знаменитый французский математик и астроном П.Лаплас (1749–1827) выразил это положение следующими словами:
Ум, которому были бы известны для какого-либо данного момента все силы, одушевляющие природу, и относительное положение всех ее составных частей, если бы вдобавок он оказался достаточно обширным, чтобы подчинить эти данные анализу, обнял бы в одной формуле движения величайших тел Вселенной наравне с движениями мельчайших атомов: не осталось бы ничего, что было бы для него недостоверным, и будущее, так же как и прошедшее, предстало бы перед его взором5.
Эта концепция получила название лапласовского детерминизма. Она является законным и неизбежным следствием механистической концепции мира. Правда, с современной точки зрения формулировка Лапласа нуждается в некотором уточнении, так как мы не можем признать законными понятия всеведущего разума и абсолютной точности измерения. Но ее легко модернизировать, практически не меняя смысла. Мы говорим, что если известны с достаточной точностью координаты и импульсы всех частиц в достаточно большом объеме пространства, то можно рассчитать поведение любой системы в любом заданном интервале времени с любой заданной точностью. Из этой формулировки, как и из первоначальной формулировки Лапласа, можно сделать вывод, что все будущие состояния Вселенной предопределены. Неограниченно повышая точность и охват измерений, мы неограниченно удлиняем сроки предсказаний. Так как никаких принципиальных ограничений на точность и охват измерений, т. е. таких ограничений, которые вытекали бы не из ограниченности человеческих возможностей, а из природы объектов измерения, не существует, мы можем представить себе предельный случай и заявить, что на самом деле все будущее мира определено уже сейчас и абсолютно однозначно. Здесь выражение «на самом деле» приобретает вполне отчетливый смысл; наша интуиция легко признает законность этого «на самом деле» и сопротивляется его дискредитации.
Итак, механистическая концепция мира приводит к представлению о полной детерминированности явлений. Но это противоречит субъективному ощущению свободы выбора, которым мы обладаем. Отсюда два выхода: признать ощущение свободы выбора «иллюзорным» или же признать механистическую концепцию негодной в качестве универсальной картины мира. Сейчас уже трудно сказать, в какой пропорции разделялись на эти две точки зрения мыслящие люди «доквантовой» эпохи. Если подходить к вопросу с современной позиции, то, даже не зная ничего о квантовой механике, надо решительно встать на вторую точку зрения. Мы понимаем сейчас, что механистическая концепция, как и любая иная концепция, является лишь вторичной моделью мира по отношению к первичным данным опыта, поэтому непосредственные данные опыта всегда обладают приоритетом перед любой теорией.
Ощущение свободы выбора есть первичный опытный факт, как и другие первичные факты духовного и чувственного опыта. Теория не может отвергнуть этого факта, она может лишь сопоставить с ним какие-то новые факты — процедура, которую мы при выполнении определенных условий называем объяснением факта. Объявить свободу выбора «иллюзорной» так же бессмысленно, как объявить человеку, у которого болит зуб, что его ощущение «иллюзорно». Зуб может быть совершенно здоров, а ощущение боли — быть результатом раздражения определенного участка мозга, однако от этого оно не становится «иллюзорным».
Квантовая механика разрушила детерминизм. Прежде всего, оказалось ложным представление об элементарных частицах как о маленьких тельцах, движущихся по определенным траекториям, а, следовательно, рухнула и вся механистическая картина мира — такая понятная, привычная и, казалось бы, совершенно несомненная. Физики XX в. уже не могут ясно и убедительно, как это умели физики XIX в., рассказать людям, что на самом деле представляет собой мир, в котором они живут. Но детерминизм рухнул не только как часть механистической концепции, но и как часть любой картины мира. В принципе можно было бы представить себе такое полное описание (картину) мира, которое включает лишь реально наблюдаемые явления, но дает однозначные предсказания всех явлений, которые когда-либо будут наблюдаться. Теперь мы знаем, что это невозможно. Мы знаем, что существуют ситуации, в которых принципиально невозможно предсказать, какое из множества мыслимых явлений осуществляется в действительности. Более того, эти ситуации являются согласно квантовой механике не исключением, а общим правилом; строго детерминированные исходы являются как раз исключением из правила. Квантово-механическое описание действительности — существенно вероятностное описание, а однозначные предсказания оно включает лишь как предельный случай.
В качестве примера рассмотрим опыт с дифракцией электронов, изображенный на рис. 13.1. Условия опыта полностью определены, когда заданы все геометрические параметры установки и начальный импульс электронов, испускаемых пушкой.
Все электроны, вылетающие из пушки и попадающие на экран, находятся в равных условиях и описываются одной волновой функцией. Между тем они поглощаются (дают вспышки) в разных точках экрана, и заранее предсказать, в какой точке даст электрон вспышку, невозможно; нельзя даже предсказать, отклонится ли он на нашем рисунке вверх или вниз, можно указать только вероятность попадания в различные участки экрана.
Позволительно, однако, задать вопрос: почему мы уверены, что если квантовая механика не может предсказать точку попадания электрона, то и никакая будущая теория не сможет сделать этого?
На этот вопрос мы дадим не один, а целых два ответа; вопрос вполне заслуживает такого внимания.
Первый ответ можно назвать формальным. Он таков. Квантовая механика основана на том принципе, что описание с помощью волновой функции является максимально полным описанием состояний квантовой частицы. Этот принцип в виде вытекающего из него соотношения неопределенностей подтвержден огромным числом экспериментов, интерпретация которых содержит понятия только низкого уровня, непосредственно связанные с наблюдаемыми величинами. Выводы квантовой механики, включающие более сложные математические расчеты, подтверждены еще большим числом экспериментов. И нет решительно никаких указаний на то, что мы должны усомниться в этом принципе. Но он равнозначен невозможности предсказаний точного исхода опыта. Например, чтобы указать точку на экране, куда попадает электрон, надо знать о нем больше, чем дает волновая функция.
Второй ответ мы начнем с того, что попытаемся понять, почему нам никак не хочется согласиться с невозможностью предсказания точки, куда попадет электрон. Столетия развития физики приучили людей к мысли, что движение неодушевленных тел регулируется исключительно внешними по отношению к ним причинами и что путем достаточно тонкого исследования эти причины можно всегда обнаружить, подсмотреть их. Это убеждение было вполне оправдано, пока считалось возможным подсматривать за системой, не влияя на нее, что имело место в опытах над макроскопическими телами.
Представьте себе, что на рис. 13.1 рассеиваются не электроны, а пушечные ядра и что вы изучаете их движение. Вы видите, что в одном случае ядро отклоняется вверх, а в другом — вниз, и вы не желаете верить, что это происходит само по себе, а убеждены, что различие в поведении ядер объясняется какой-то реальной причиной. Вы снимаете полет ядра на кинопленку или предпринимаете еще какие-то действия и, в конце концов, находите такие явления A1 и A2, связанные с полетом ядра, что при наличии A1 ядро отклоняется вверх, а при наличии A2 — вниз. И вы говорите, что A1 — причина отклонения ядра вверх, а A2 — причина отклонения вниз. Возможно, что ваша камера окажется несовершенной или вам просто надоест исследование и вы не найдете искомой причины. Но вы все-таки останетесь в убеждении, что на самом деле причина существует, т. е. если бы вы получше посмотрели, то явления A1 и A2 были бы обнаружены.
Как же обстоит дело в опыте с электронами? Вы снова видите, что электрон в одних случаях отклоняется вверх, в других — вниз и в поисках причины пытаетесь проследить за его движением, подсмотреть за ним. Но тут оказывается, что вы не можете подсмотреть за электроном, не влияя на его судьбу самым катастрофическим образом. Чтобы «увидеть» электрон, надо направить на него поток света. Но свет взаимодействует с веществом порциями, квантами, которые подчиняются тому же самому соотношению неопределенностей, что и электроны, и другие частицы. Поэтому с помощью света, а также с помощью любых других средств исследования выйти за пределы соотношения неопределенностей не удается. Пытаясь уточнить координату электронов с помощью фотонов, мы либо сообщаем ему такой большой и неопределенный импульс, который портит весь эксперимент, либо измеряем координату так грубо, что не узнаем о ней ничего нового. Таким образом, явлений A1 и A2, т. е. причин, по которым электрон в одних случаях отклоняется вверх, а в других случаях вниз, не существует в действительности. А утверждение, что «на самом деле» какая-то причина есть, теряет всякий научный смысл.
Итак, существуют явления, у которых причин нет, точнее, существует ряд возможностей, из которых одна осуществляется без всякой причины. Это не значит, что принцип причинности вообще следует отбросить: в том же опыте если отключить электронную пушку, то вспышки на экране вообще исчезнут и причиной их исчезновения будет отключение пушки. Но это значит, что его надо существенно ограничить по сравнению с тем, как он понимался в классической механике и как он до сих пор понимается обыденным сознанием. У некоторых явлений причин нет, их надо принимать просто как нечто данное. Таков уж мир, в котором мы живем.
Второй ответ на вопрос о причинах нашей уверенности в существовании непредсказуемых явлений состоит в том, что с помощью соотношения неопределенностей мы уясняем себе не только массу новых фактов, но и природу того перелома в отношении причинности и предсказуемости, который происходит при вторжении в микромир. Мы видим, что вера в абсолютную причинность проистекала из молчаливого предположения о наличии бесконечно тонких средств исследования, «подсматривания» за объектом. Но, дойдя до элементарных частиц, физики обнаружили, что существует минимальный квант действия, измеряемый постоянной Планка, и это создает порочный круг при попытках детализировать сверх меры описание одной частицы с помощью другой. И абсолютная причинность рухнула, а вместе с ней и детерминизм. С общефилософской точки зрения представляется вполне естественным, что если не существует бесконечной делимости материи, то не существует и бесконечной детальности описания, так что крушение детерминизма представляется более естественным, чем если бы он сохранился.
Квант развития
Давно подмечено сходство между последовательными этапами развития техники и функциями биологических объектов. Производство технических материалов можно сопоставить образованию и росту живой ткани. Использование двигателей соответствует работе мышц. Автоматическое управление и передача информации соответствуют функционированию нервной системы. Эта параллель существует, несмотря на коренное различие в природе биологических и технических систем и совершенно различные причины, вызывающие их развитие. Тем не менее сходство в стадиях развития отнюдь не является случайным. Оно вытекает из наличия у всех процессов развития одной обшей черты: развитие всегда происходит путем последовательных метасистемных переходов. Метасистемный переход — это, если угодно, элементарная единица, универсальный квант развития. Поэтому нет ничего удивительного, что, сопоставив начальные стадии развития двух разных систем, например технический материал и живую ткань, мы получаем естественное сопоставление следующих стадий, которые образуются накоплением этих универсальных квантов.
Кванторы
В математике большую роль играют утверждения о всеобщности данного свойства и о существовании хотя бы одного объекта, обладающего данным свойством. Для записи этих утверждений вводятся так называемые кванторы: квантор всеобщности ? и квантор существования ?. Допустим, что некоторое высказывание S содержит переменную (неопределенный объект) х, поэтому будем записывать его в виде S(x). Тогда высказывание
(?x)S(x)
означает, что для всех х имеет место S(x), а высказывание
(?x)S(x)
состоит в утверждении, что существует хотя бы один объект х такой, что для него верно высказывание S(x).
Переменная, входящая в высказывание под знаком квантора, называется связанной переменной, ибо высказывание от этой переменной не зависит, подобно тому как сумма
i=n? mSi
не зависит от индекса i. Связанную переменную можно заменить любой другой буквой, не совпадаюшей с остальными переменными, и от этого смысл высказывания не изменится. Переменная, которая не является связанной, называется свободной. Высказывание зависит только от свободных переменных, которые оно содержит.
Примеры высказываний с кванторами:
(?х)(?у)(«брат»(х, у) ? «мужчина»(у)) ? «брат»(у, x).Для всякого х и всякого у, если х — брат у и у — мужчина, то у — брат x. Если через D(x, y) обозначить высказывание «x является делителем у», то одно из соотношений, приведенных выше в качестве примера высказываний, изобразится в виде
(?n)(>(n, «1») ? (?p)D(p, n)). (?x)W(x) ? ¬(?x) ¬W(x).
Это соотношение верно для любого высказывания W(x) и показывает, что имеет место связь между кванторами существования и всеобщности. Из существования объекта х, для которого верно W(x), следует, что неверно утверждение, будто для всех х W(x) неверно.
Квантор — это тоже в сущности логическая связка. Приписывание квантора превращает высказывание в новое высказывание, которое содержит на одну свободную переменную меньше. Отличие от связок, которое мы рассматривали выше, состоит в том, что, кроме высказывания, надо указать еще свободную переменную, которую надо связать. Связывание переменной подразумевает подстановку вместо нее конкретных объектов. Если число объектов, которые могут быть подставлены вместо переменной, конечно, то кванторы можно рассматривать просто как удобные сокращения, ибо они могут быть выражены через логические связки — конъюнкцию и дизъюнкцию. Пусть переменная х может принимать n значений, которые мы обозначим буквами х1, х2,..., xn. Тогда имеют место следующие эквивалентности:
(?x)W(x) ? W(x1) ? W(x2) ? ... ? W(xn),
(?x)W(x) ? W(x1) ? W(x2) ? ... ? W(xn).
Лейтмотив новой математики
Суть того, что произошло в математике в XVII в., — овладение общим принципом использования формализованного языка, давшее начало движению вверх по лестнице, которое привело к грандиозным достижениям и продолжается до настоящего времени. Правда, тогда этот принцип не был так четко сформулирован, как это мы делаем теперь, и сам термин «формализованный язык» появился только в XX в. Но фактически он использовался. Реформа Декарта, как мы видели, была первым шагом на этом пути. Сочинения Декарта и, в частности, цитаты, приведенные выше, показывают, что этот шаг отнюдь не был случайным, а вытекал из его метода познания законов природы, который, если сформулировать его в современных терминах, и есть метод создания моделей с помощью формализованного языка. Декарт сознает общность своего метода и его «математичность». В «Правилах для руководства ума» он высказывает уверенность, что должна существовать «некая общая наука, объясняющая все, относящееся к порядку и мере, не входя в исследование никаких частных предметов». Эту науку, пишет он, следует назвать «всеобщей математикой».
Другой великий математик-философ XVII в. г. Лейбниц (1646–1716) уже полностью понимает значение формализации языка и мышления. В течение всей жизни Лейбниц разрабатывал символическое исчисление, названное им «универсальной характеристикой», целью которого было выражать все ясные человеческие мысли и сводить логические умозаключения к чисто механическим операциям. В одной из своих ранних работ он заявляет:
Истинный метод должен дать нам нить Ариадны, т. е. некое осязаемое и грубое средство, которое направило бы разум, подобно начертанным линиям в геометрии и формам операций, предписываемым обучающимся арифметики. Без этого наш разум не смог бы проделать длинный путь, не сбившись с дороги.
Это, по существу, указание на роль формализованного языка как материального фактора понятий-конструктов, т. е. на его главную роль. Н.Бурбаки в историческом очерке об основании математики пишет:
Многочисленные места из сочинений Лейбница, в которых он упоминает о своем грандиозном проекте и о прогрессе, который последует за его реализацией, показывают, с какой ясностью он понимает формализованный язык как чистую комбинацию знаков, в которых имеет значение лишь их сцепление, так что машина сможет получать все теоремы и все недоразумения смогут быть разрешены простым вычислением.
Хотя подобные чаяния и могут показаться чрезмерными, все же надо признать, что, находясь именно под их постоянным воздействием, Лейбниц создал значительную часть своих математических трудов и прежде всего свои работы по символике исчисления бесконечно малых. Он сам это прекрасно сознавал и явно связывал свои идеи о введении индексов и детерминантов и свой набросок «Геометрическое исчисление» со своей «характеристикой». Но он считал, что его наиболее значительным трудом будет символическая логика... и хотя ему не удалось создать подобного исчисления, он по крайней мере трижды приступал к реализации своего намерения2.
Идеи Лейбница об «универсальной характеристике» в свое время не получили развития. Дело формализации логики сдвинулось с мертвой точки только во второй половине XIX в. Но идеи Лейбница — свидетельство того факта, что принцип описания действительности с помощью формализованного языка есть врожденная особенность европейской математики, которая всегда была источником ее развития, хотя авторами осознавалась в различной степени.
В наши цели не входит изложение истории современной математики, как и подробное описание понятий, лежащих в ее основе: для этого понадобилась бы отдельная книга. Нам придется удовлетвориться кратким очерком, затрагивающим лишь тот аспект математики, который в первую очередь интересует нас в данной книге, а именно системный аспект.
Лейтмотивом развития математики в течение последних трех столетий было постепенно углубляющееся осознание математики как формализованного языка и вытекающее отсюда возрастание ее «многоэтажности», происходящее путем метасистемных переходов различного масштаба.
В оставшейся части настоящей главы мы рассмотрим важнейшие проявления этого процесса, которые можно назвать вариациями на основную тему, исполняемыми на различных инструментах и в различном сопровождении. Одновременно с ростом здания математики ввысь происходило расширение всех его этажей, в том числе самого нижнего, т. е. сферы приложений.
Лингвистическая относительность
Из всего сказанного вовсе не следует, что объективизация времени — это зло, от которого надо отказаться и перейти на язык типа хопи. Напротив, с объективизацией времени связаны важнейшие черты европейской культуры, которые обеспечили ей столь выдающееся место: историчность (интерес к прошлому, датировка, летопись) и развитие точных наук. Наука в том виде, который нам пока только и известен, не могла бы существовать без объективизации времени. Сопоставление временных отношений пространственным отношениям и следующий за этим шаг — измерение времени — это конструирование определенной модели чувственного опыта. Быть может, это первая модель, создаваемая на уровне языка. Как и всякая модель, она содержит элемент произвола и насилия над действительностью. Но это не значит, что ее надо отбросить. Ее надо улучшать, это верно, но не просто отбрасывать. А чтобы улучшать, надо прежде всего осознавать ее как модель, а не как первичную данность. В этом отношении лингвистический анализ чрезвычайно полезен, ибо он учит отличать относительное от абсолютного, учит видеть относительное и условное в том, что на первый взгляд представляется абсолютным и безусловным. Свою концепцию Уорф так и назвал концепцией лингвистической относительности.
Здесь имеет место любопытная перекличка с физической теорией относительности. Объективизированное время — это основа классической ньютоновской механики. Поскольку воображаемое пространство, в котором мы проектируем время, никак не связано с реальным пространством, мы представляем себе время как что-то такое, что «течет» одинаково во всех точках реального пространства. Эйнштейн осмелился пересмотреть это представление и показал, что оно не содержится в опытных данных и что от него следует отказаться. Но этот отказ, как хорошо известно, дается не без труда. Почему же? Уорф пишет:
Импровизированный ответ, возлагающий всю вину за нашу медлительность в постижении таких тайн космоса, как, например, относительность, на интуицию, является ошибочным. Правильно ответить на этот вопрос надо так: ньютоновские понятия пространства, времени и материи не есть данные интуиции. Они даны культурой и языком. Именно из этих источников и взял их Ньютон.
Здесь опять следует смягчить высказывания увлекающегося лингвиста. Ньютоновские понятия, конечно, непосредственно опираются на нашу интуицию. Но сама эта интуиция не есть чистое отражение первичного чувственного опыта, «калейдоскопического потока впечатлений», а есть продукт его организации и в этой организации язык и культура действительно играют далеко не последнюю роль.
Логические связки
Широко употребительных логических связок пять. Это отрицание (изображается знаком ¬), конъюнкция (знак ?), дизъюнкция (знак ?), импликация (знак ?) и эквивалентность (знак ?).
Высказывание ¬A (читается «не A») означает, что высказывание A ложно. Иначе говоря, ¬A истинно тогда, когда A ложно, и ложно тогда, когда A истинно.
Высказывание A ? B (читается «A и B») означает утверждение, что верно и A, и B. Оно верно только в том случае, если верны оба высказывания A и B.
Высказывание A ? B («A или B») верно, если верно хотя бы одно из высказываний A и B.
Высказывание A ? B читается «A влечет B» или «если A, то B». Оно неверно, если A истинно, B ложно, и верно во всех остальных случаях.
Наконец, высказывание A ? B верно в том случае, если высказывания A и B либо оба истинны, либо оба ложны.
Для обозначения структуры связей пользуются скобками подобно тому, как это делается в алгебре для обозначения порядка выполнения арифметических действий. Так, например, высказывание ¬A ? B означает «A неверно, а B верно», а высказывание ¬(A ? B) — «неверно, что A и B оба верны». И так же, как в алгебре, для уменьшения числа скобок устанавливается порядок старшинства связок по силе связи. Выше мы перечислили связки в порядке ослабления связи. Например, конъюнкция связывает сильнее, чем импликация, поэтому высказывание A ? B ? C понимается как A ? (B ? C), но не как (A ? B) ? C. Это соответствует тому, что в алгебре a + b × c означает a + (b × c), но не (a + b) × c.
Приведем несколько примеров составных высказываний.
Известная скороговорка утверждает: «цапля чахла, цапля сохла, цапля сдохла». Это высказывание можно записать в виде: «цапля чахла» ? «цапля сохла» ? «цапля сдохла».
Соотношение 0 < Z < 1 есть конъюнкция «Z > 0» ? «Z < 1», a соотношение |Z| > 1 — дизъюнкция «Z > 1» ? «Z < -1». Определение логической связки ? данное выше, можно записать так:
[(A ? B) ? (A ? B) ? (¬A ? ¬B)] ? [(A ? B) ? (¬A ? ¬B) ? (A ? B)]
Предоставляем читателю перевести на обычный язык следующее высказывание:
«Свет включен» ? «Лампочка не горит» ? «Нет электричества» ? «Перегорели пробки» ? «Перегорела лампочка».
Если считать, что высказывания могут быть только истинными или ложными и, сверх этого, о высказывании ничего сказать нельзя, то перечисленных связок достаточно, чтобы выразить все мыслимые конструкции из высказываний. Достаточно даже двух связок, например отрицания и конъюнкции или отрицания и дизъюнкции. Такая ситуация имеет место, в частности, в отношении утверждений математики. Поэтому в математической логике других связок не используется.
Однако естественный язык отражает большее разнообразие в оценке высказываний, чем просто деление их на истинные и ложные. Например, высказывание можно рассматривать как бессмысленное или как недостоверное, хотя и возможное («в этом лесу, наверное, есть волки»). Этим вопросам посвящены специальные разделы логики, в которых находятся другие связки. Большого значения для современной науки эти разделы (в отличие от классической математической логики) не имеют, и мы их касаться не будем.
Логический анализ языка
Итак, для логического анализа, т. е. для построения логического эквивалента фразы естественного языка, мы должны прежде всего провести синтаксический анализ фразы; результаты анализа непосредственным образом отразятся на синтаксической структуре логического выражения. Но и семантика отнюдь не останется в стороне. Когда мы говорим, что «рыжий» — это одноместный предикат, «загрыз» — двуместный предикат, «расстояние» — функция, «и» — логическая связка, «все» — квантор и т.д., мы выполняем семантический анализ понятий, выражаемых естественным языком. Мы классифицируем понятия в соответствии со схемой, зафиксированной в языке логики, и устанавливаем связь между понятиями. Логический анализ — это по существу семантический анализ. Синтаксический анализ нужен постольку, поскольку он необходим для семантического.
Логический анализ может быть более или менее глубоким. В нашем примере он весьма поверхностен. Посмотрим, могли бы мы его продолжить, и если да, то как именно.
Понятия «пес», «рыжий» и «кошка» — одноместные предикаты, которые можно признать элементарными и не подлежащими дальнейшему анализу. Это простые аристотелевские понятия, опирающиеся непосредственно на чувственный опыт; каждый нормальный человек умеет их распознавать, и единственный способ объяснить, что такое «кошка», — это показать кошку.
Понятие «бродячая» — тоже одноместный предикат, но уже более сложный. Рассуждая формально грамматически, можно было бы заключить, что «бродячая» означает «которая бродит». Но это было бы неверным заключением, ибо глагол «бродит» не указывает длительности время провождения, которое он именует. Вполне добропорядочная семейная кошка может выйти на часок побродить по крыше, и это никому не дает права назвать ее «бродячей». Правильнее определить бродячую кошку как кошку, у которой нет хозяина, или же, пользуясь отношением, которое уже входит в наше логическое выражение, как кошку, которая никому не принадлежит. Вот формальная запись этого определения:
«бродячий»(x) ? ¬(?y)(«принадлежит»(x, y)).
(Здесь подразумевается, что х — произвольный объект.)
Обратимся к отношению «принадлежит». Мы ввели его, в некотором смысле, контрабандой, ибо слова «принадлежать» не было в исходной фразе. Но оно подразумевалось и семантический анализ выявил его! Отношение принадлежности передавалось в русской фразе родительным падежом. Здесь мы видим яркий пример неоднозначности и недостаточности синтаксического анализа. Тот же самый родительный падеж, который используется в конструкции «собака вдовы», используется в конструкции «хозяйка собаки», но никак нельзя сказать, что хозяйка «принадлежит» своей собаке. Конструкцию «нос вдовы» можно, конечно, истолковать как «нос, который принадлежит вдове». Но здесь мы уже встречаемся, с семантической неоднозначностью слова «принадлежит», ибо нос, очевидно, принадлежит вдове не так, как принадлежит ей собака.
Чтобы разложить понятие «принадлежит» на элементарные составные части, надо проделать изрядную работу: описать обычаи и законы, связанные с правом собственности. Только в этом случае можно объяснить, что значит «принадлежит». Предикат «вдова» и функции «чин» и «фамилия» (которые мы уже ввели, анализируя понятие «поручик Пшебысский») также связаны с социальной сферой и требуют дальнейшего анализа. Наконец, понятие «загрыз», хотя оно и не связано с социальной сферой и явно проще (ближе к чувственному опыту), чем предыдущие понятия, также могло бы быть подвергнуто логическому анализу. В нем можно выделить, во-первых, элемент завершенности действия, выражающийся глагольной формой, во-вторых, конечный результат — смерть жертвы и, в-третьих, характерную особенность действия — использование зубов.
Логический анализ языка — чрезвычайно интересное направление исследований, но мы не можем останавливаться на нем более фундаментально. Интересующихся отошлем к книге одного из основоположников этого направления Г.Райхенбаха1.
Итог сравнения естественного языка и языка логики подведем следующим образом. Язык логики обладает простым и полностью формализованным синтаксисом.Текст на естественном языке можно путем синтаксического и семантического анализа перевести на язык логики, т. е. сопоставить ему текст на языке логики, имеющий тот же смысл. Семантический анализ естественного текста при переводе может быть более или менее глубоким, т. е. предикаты и функции, входящие в логический текст, могут быть ближе или дальше от непосредственного чувственного и духовного опыта. Существуют такие предикаты и функции, которые разложимы на более элементарные слагающие и которые поэтому нельзя определить иначе, как сославшись на опыт. Такие предикаты и функции мы будем называть первичными.
1 Reihenbuch H. Elements of symbolic logic. New York, 1960.
Логическое понятие
Мы почти закончили анализ основ логики с той точки зрения, которая рассматривает мозг как черный ящик. Осталось только определить общее понятие «логическое понятие». Определение это просто: понятие — это предикат или логическая связка. Основание таково: предикаты и связки — это те базисные функциональные узлы, которые мы обнаруживаем в языковой деятельности. Понятие функции в том смысле, как мы его определили выше, можно не возводить в ранг основного логического понятия, так как оно, как мы видели, выразимо через предикаты и связки. Но в более широком смысле и логические связки, и предикаты являются функциями, т. е. определенным способом сопоставления значений (истинных в данном случае) аргументам. Поэтому можно сказать, что логическое понятие — это функция, аргументы которой — языковые объекты и ситуации, а значения — языковые объекты. Результатом логического анализа языка является разложение языковой деятельности на однотипные функциональные элементы — связки и предикаты.
Каждое логическое понятие определяется, во-первых, своим материальным носителем — языковым объектом (в большинстве словом или словосочетанием) и, во-вторых, способом использования этого объекта в общественной языковой деятельности. Второй пункт дает возможность уточнить первый: слова «кошка», «кошка», «кошка», «КОШКА» — это разные языковые объекты (первые два отличаются положением в пространстве, третье и четвертое, вдобавок, шрифтом), но мы считаем их носителями одного понятия, ибо в языковой деятельности они выступают как неразличимые. То же с известными ограничениями (но только с ограничениями!) можно сказать о слове «die Katze» немецкого языка, ибо оно используется аналогично (но только аналогично!) слову «кошка» в русском языке.
Понятия языка образуют иерархическую систему. В некоторых специализированных языках (подъязыках), используемых точными науками, эта иерархия определена совершенно явно и строго. Понятия, расположенные выше в иерархии, приобретают смысл логических определений через понятия более низкого уровня, т.
е. указывается, каким образом, умея определять истинностные значения предикатов более низкого уровня, можно определить значение предиката более высокого уровня. В естественных языках строгой иерархии нет, но есть иерархия приблизительная. Это значит, что мы можем оценить «степень удаленности» понятия от непосредственных данных опыта путем логического анализа и расщепления сложных понятий на более простые компоненты; степень удаленности понятия от непосредственного опыта можно отождествить с высотой положения в иерархии. Так как расщепление на компоненты неоднозначно, сам способ расщепления не полностью формализован и, наконец, никто еще не выполнял такой работы для всего языка, оценка положения в иерархии приблизительна. Пожалуй, наиболее твердо установленным фактором является первичность (принадлежность к нижнему уровню иерархии) ряда предикатов, которые никак не поддаются расщеплению.
Между понятиями языка существуют многочисленные перекрестные связи, которые задаются множеством всех истинных высказываний, в которые входят рассматриваемые понятия. Язык — это система, и понятия его имеют смысл только как элементы системы. Значение слова определяется тем, как это слово используется в языковой деятельности. Каждое слово как бы несет на себе отпечаток всех предложений, в которые оно когда-либо входило, оно элемент системы. В традиционной логике, когда говорят о понятиях, указывают на две функции понятия: служить элементом суждения, т. е. способом формирования мысли, и в то же время концентрировать в себе уже имеющиеся мысли, знания о предмете. Эта двойственность является следствием системного характера понятия. Языковый объект (слово), выражающий понятие, используется как элемент для построения модели действительности и ассоциируется функционально, т. е. в языковой действительности (а следовательно, и в нашем воображении), со всеми моделями, в которых он участвует. Поэтому, хотя натренированная собака и отличает квадрат от круга, нельзя сказать, что она владеет понятием «квадрат»: это слово включает в себя множество вещей, о которых собака не имеет ни малейшего представления.Поэтому же наиболее точный перевод с одного языка на другой — это далеко не всегда буквальный перевод: необходимо учесть различие систем. Строго говоря, абсолютно точный перевод вообще невозможен (за исключением, быть может, высказываний, содержащих лишь первичные понятия, доступные собаке).
Магия слов
На стадии первобытного мышления ассоциация имя-значение Li - Ri уже существует, ибо язык прочно вошел в жизнь, но она еще не стала объектом внимания, ибо метасистемный переход на второй уровень языковой деятельности пока не произошел. Поэтому ассоциация Li - Ri воспринимается в точности так же, как любая ассоциация Ri - Rj между элементами действительности, например ассоциация молния-гром. Для первобытного мышления связь между объектом и его именем — абсолютная, физическая, так сказать, реальность, усомниться в которой просто невозможно. Фактически — и это вытекает из фундаментального свойства ассоциации — первобытный человек мыслит себе единый объект Li - Ri, у которого имя Li и материальный облик Ri, суть различные части или стороны. О таком отношении к именам среди первобытных народов свидетельствует множество исследователей.
Индеец рассматривает свое имя не как простой ярлык, но как отдельную часть своей личности, как нечто вроде своих глаз или зубов. Он верит, что от злонамеренного употребления его имени он так же верно будет страдать, как от раны, нанесенной какой-нибудь части его тела. Это верование встречается у разных племен от Атлантического до Тихого океана (Дж.Муни).
Потому у многих народов распространен обычай пользоваться в быту не «настоящим» именем человека, а его прозвищем, которое рассматривается как нечто случайное и произвольное. Исследователь народов Западной Африки А.Б.Эллис утверждает, что среди них
существуют верования в реальную и физическую связь между человеком и его именем: можно ранить человека, пользуясь его именем... Настоящее имя царя является тайным... Может показаться странным, что только имя, дающееся при рождении, а не повседневное имя, считается способным переносить в другое место часть личности... Дело в том, однако, что туземцы, по-видимому, думают, будто повседневное имя не принадлежит реально человеку.
Это разделение имен на «настоящие» и «ненастоящие» является, очевидно, первым шагом на пути к метасистемному переходу.
Отношение между предметом и его изображением воспринимается точно так же, как между предметом и его именем. Вообще никакого существенного различия между изображением и именем первобытное мышление не проводит. Это и неудивительно, ибо изображение связано с оригиналом такой же ассоциацией, как и имя. Изображение — это имя, имя — изображение. Все изображения и имена предмета образуют вместе с самим предметом нечто целое, единое (а именно представление, созданное ассоциацией). Поэтому кажется очевидным, что действуя на часть, мы тем самым действуем и на целое, а значит, и на другие его части. Изображая бизона, пронзенного стрелой, человек верит, что он тем самым способствует успешной охоте на реального бизона. Художник и ученый Дж.Кетлин, живший среди манданов (Северная Америка), рассказывает, что манданы верили, что рисунки (и, в частности, портреты), сделанные им, заимствовали у своих оригиналов какую-то часть жизненного начала. «Я знаю, — говорил один из манданов, — что этот человек уложил в свою книгу много наших бизонов, я знаю это, ибо я был при том, когда он это делал, с тех пор у нас нет больше бизонов для питания». Очевидно, этот индеец понимал, что белый человек не укладывал бизонов в книгу в буквальном смысле, в их, так сказать, материальном виде, но ему было очевидно, что в некотором смысле, а именно по отношению к комплексам «реальный бизон — рисунок бизона», белый человек все-таки уложил бизонов в книгу, поэтому их стало меньше. Слово «уложил» используется при этом в несколько метафорическом смысле, если основной смысл относить к действию над «материальным» бизоном, но это не влияет на верность мысли. Множество терминов во всех языках мира используются метафорически, без этого было бы невозможно развитие языка. Когда мы говорим «эти мысли хорошо уложились у меня в голове», то это не значит, что они уложились точно так, как укладываются в чемодане вещи.
Масштаб метасистемного перехода
Нас больше интересует случай, когда переход на следующую ступеньку является качественным, а именно метасистемным переходом. Чтобы в этом случае мог иметь место эффект лестницы, необходимо, очевидно, чтобы система X, претерпевающая метасистемный переход (рис. 5.2), сама оставалась бы подсистемой какой-то более обширной системы Y, в рамках которой обеспечиваются и поддерживаются условия для многократного перехода «со ступеньки на ступеньку» — метасистемного перехода над подсистемой X. Такую систему Y мы называем ультраметасистемой по отношению к ряду X, X', X'',... и т. д. Рассмотрим подробнее вопрос о связи между метасистемным переходом и отношением система — подсистема.
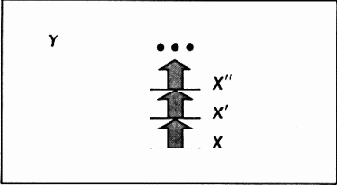
Рис. 5.2. Эффект лестницы в рамках ультраметасистемы Y. Стрелки указывают изменения, происходящие со временем
Мы уже встречались с метасистемными переходами различной масштабности. Метасистемные переходы в структуре мозга совершаются в рамках организма, они не затрагивают организма в целом. Социальная интеграция — это метасистемный переход по отношению к организму в целом, но она не выводит человечество за пределы биогеоценоза — системы взаимодействующих живых существ в масштабе Земного шара. Всегда существует система Y, которая включает данную систему Х в качестве своей подсистемы. Единственным исключением, быть может, является Космос в целом — система Z, которая по определению не входит в состав никакой другой системы. Мы говорим «быть может» потому, что не знаем, можно ли рассматривать Космос как систему в том же смысле, как заведомо конечные системы.
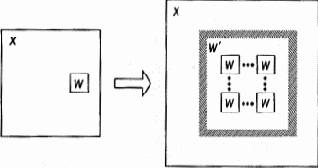
Рис. 5.3. Метасистемный переход W > W' в рамках системы Х
Теперь обратим наш взгляд в противоположном направлении — от большого к малому, от целого к части. Что происходит с системой X, когда она эволюционирует, не претерпевая метасистемного перехода? Допустим, что некая подсистема W системы Х совершает метасистемный переход (рис. 5.3). Это значит, что вместо W появляется система W', которая по отношению к W является метасистемой и содержит целый ряд подсистем типа W, но по отношению к Х является подсистемой, аналогичной W, и выполняет те же функции в Х, которые прежде выполняла W, только, вероятно, лучше.
В зависимости от роли подсистемы W в системе Х
замена W на W' будет иметь для Х большее или меньшее значение. Разбирая этапы эволюции живых существ кибернетического периода, мы на место Х подставляли организм в целом, а на место W — высший этаж управления организмом.
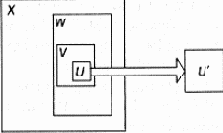
Рис. 5.4. Метасистемный переход на одном из низших уровней организации
Поэтому и метасистемный переход W > W' имел первостепенное значение для X. Однако метасистемный переход может произойти где-то «в провинции», на одном из низших уровней организации (рис. 5.3). Пусть W — одна из подсистем X, V — одна из подсистем W, U — одна из подсистем V. Метасистемный переход U > U' может сильно улучшить функционирование V, а, следовательно, и функционирование W, хотя уже в меньшей степени, и, наконец, еще в меньшей степени > функционирование X. Итак, эволюционные сдвиги в X, даже не очень значительные, могут быть вызваны метасистемным переходом только на одном из низших уровней структуры.
Эти наблюдения дают новый материал для оценки количественных и качественных изменений в процессе развития. Если система Х содержит однородные подсистемы W и число этих подсистем увеличивается, мы называем такое изменение количественным. Метасистемный переход мы, без сомнения, относим к качественным изменениям. Можно предположить, что всякое качественное изменение вызывает метасистемный переход на том или ином уровне структуры системы. Учитывая описанную выше механику эволюции (редупликация системы плюс метод проб и ошибок), это предположение представляется весьма вероятным.
Математическая логика
Решающим фактором в прогрессе логики была ее математизация (конец XIX – начало XX вв.). Математизация логики была порождена потребностями математики и осуществлена математиками. Разрыв между математикой и логикой был, наконец, преодолен. Расширив свой язык и математизировав его, логика стала пригодной для описания и исследования математического доказательства. С другой стороны, для решения логических проблем стали применяться математические методы.
Завоевав плацдарм в области математики, новая логика стала проникать в естественные науки и философию. При этом роль собственно математического элемента (использование математических моделей) упала. Тем не менее всю современную логику часто называют «математической» по причине ее языка и происхождения.
Материальная и духовная культура
Различают культуру «материальную» и «духовную». Мы поместили эти слова в кавычки (для первого раза; дальше они, как и принято, будут щеголять без кавычек), потому что различие между указанными проявлениями культуры условно, а сами термины не слишком удачно отражают это различие. К материальной культуре относят производительные силы общества и все, что с ними связано, а к духовной — искусство, религию, науку, философию. Если пытаться сформулировать принцип, на основании которого делается разграничение, то лучше всего, вероятно, это сделать следующим образом: материальная культура призвана удовлетворять те потребности, которые общи у человека и животных («материальные» потребности), духовная — потребности специфические, как мы думаем, для человека («духовные» потребности). Очевидно, это различие не совпадает с различием между материальным и духовным в философском плане.
Основным предметом настоящей книги является феномен науки, которая есть часть духовной культуры. Однако наука возникает на сравнительно позднем этапе развития общества и мы никак не можем добраться до этого момента, ибо для нашей цели нужно обрисовать все предшествующие этапы. Вот и сейчас мы не можем пройти мимо материальной культуры, не сказав о ней хотя бы несколько слов. Тем более что в развитии материальной культуры мы обнаруживаем один в высшей степени интересный эффект, к которому приводит иногда метасистемный переход.
Метаматематика
Формализация логики была начата (если не считать первых попыток Лейбница) в середине XIX в. работами Дж.Буля (1815-1864) и закончена к началу XX в. главным образом благодаря работам Шредера, К.С.Пирса, Фреге и Пеано. В фундаментальном труде Рассела и Уайтхеда «Principia Mathematica» (вышел в 1910 г.) уже используется формализованный язык, который, если не считать несущественных вариаций, является общепринятым по настоящее время. Этот язык мы описали в главе 6, теперь мы дадим краткий набросок формализации логического вывода.
Существует несколько эквивалентных друг другу формальных систем логического вывода. Мы остановимся на самой компактной. Она использует всего одну логическую связку — импликацию ? и один квантор — квантор общности ?. Зато она включает логическую константу, которая изображается символом 0 и обозначает тождественно ложное высказывание. Используя эту константу, можно описать отрицание высказывания p как p ? 0, а из отрицания и импликации легко построить и остальные логические связки. Квантор существования выражается через отрицание и квантор общности, таким образом, наш сжатый язык эквивалентен полному языку, рассмотренному в главе 6.
Формальная система (языковая машина) содержит пять схем аксиом и два правила вывода. Схемы аксиом таковы:
A1. p ? (q ? p).
A2. [p ? (q ? r)] ? [(p ? q) ? (p ? r)].
A3. [(p ? 0) ? 0] ? p.
A4. (?x)[p ? q(x)] ? [p ? (?x)q(x)].
A5. (?x)q(x) ? q(t).
Здесь р, q, r — произвольные высказывания: в схемах А4 и А5 запись q(x) означает, что выделена одна из свободных переменных, от которых зависит высказывание q; запись q(t) означает, что вместо этой переменной подставлен произвольный терм t; наконец, в схеме А4 предполагается, что переменная х не входит свободно в высказывание р.
Выражение «схема аксиом» означает, что высказывание, имеющее вид одной из формул А1 — А5, рассматривается как логическая аксиома. Легко убедиться, что эти аксиомы соответствуют нашей интуиции. Схемы А1 — A3
затрагивают только исчисление высказываний, и их истинность можно проверить по таблицам истинности логических связок.
Оказывается, что они истинны всегда независимо от того, какие истинностные значения принимают высказывания р, q и r. Схема А4 гласит, что если q(x) следует при любом х из высказывания р, которое от х не зависит, то из р следует справедливость q(x) при любом х. Схема А5
— это фактически определение квантора общности: если q(x) верно для всех х, то оно верно и для любого t.
Правила вывода можно кратко записать следующим образом:
|
МР. |
|
|
GN. |
|
Логическим выводом формулы q из множества формул Х (посылок) называется конечная последовательность формул
D = (d1, d2, ..., dn)
такая, что dn совпадает с q и каждая формула di, есть либо формула из множества посылок X, либо логическая аксиома, либо заключение, полученное по правилам вывода из предыдущих формул dj. Когда мы рассматриваем аксиоматическую теорию, то в качестве множества Х фигурирует совокупность всех аксиом данной теории, а логический вывод некоторой формулы есть ее доказательство.
Итак, доказательство формулы само стало формальным объектом, формулой определенного вида (последовательность логических высказываний), вследствие чего возникла возможность чисто синтаксического исследования доказательств как свойств некоторой языковой машины. На эту возможность указал Д.Гильберт (1862–1943), крупнейший математик XX в., который вместе со своими учениками и заложил основы нового направления. Гильберт ввел понятие метаязыка и назвал новое направление метаматематикой.
Термин метасистема, который мы ввели в начале книги (и который сейчас является общепринятым), возник в результате обобщения терминологии Гильберта. Действительно, переход к исследованию математическими средствами математических доказательств – яркий пример крупномасштабного метасистемного перехода.
Основная цель, которую преследовала программа, намеченная Гильбертом, это доказательство непротиворечивости различных систем аксиом. Система аксиом называется противоречивой, если из нее можно вывести некоторую формулу q и ее отрицание ¬q. Легко показать, что если существует хотя бы одна такая формула, т. е. если теория противоречива, то из нее можно вывести любую формулу. Поэтому для аксиоматической теории вопрос о непротиворечивости системы аксиом, на которых она основана, имеет чрезвычайно большое значение. Этот вопрос допускает чисто синтаксическую трактовку: можно ли из заданных формул (наборов знаков), действуя по заданным формальным правилам, получить заданный формальный результат? Из такой постановки вопроса и исходил Гильберт; затем оказалось, что существуют и другие важные свойства теорий, которые можно исследовать синтаксическими методами. На этом пути было получено много интереснейших и важнейших результатов, главным образом негативного характера; однако мы не можем здесь на них останавливаться.
Метасистемный переход
Как уже было сказано, описание следующих этапов развития нервной системы мы будем проводить в плане более феноменологическом. Для этого нам надо подытожить результаты исследования механизма эволюции на ранних этапах в терминах общих кибернетических понятий. Начав думать в этом направлении, мы легко обнаружим одну общую черту в переходах от низшего этапа к высшему. А именно все эти переходы совершаются следующим образом. На каждом этапе биологическая система имеет подсистему, которая может быть названа высшим управляющим устройством и которая имеет наиболее позднее происхождение и наиболее высокую организацию. Переход на следующий этап происходит путем размножения этих подсистем (путем многократной редупликации) и интеграции их, т. е. объединения в одно целое с образованием (по методу проб и ошибок) системы управления, во главе которой стоит новая подсистема, которая теперь является высшим управляющим устройством нового этапа эволюции. Систему, состоящую из управляющей подсистемы Х и управляемых ею многих однородных подсистем A1, A2, A3,… мы назовем метасистемой по отношению к системам A1, A2, A3,… Переход с этапа на этап мы назовем, следовательно, метасистемным переходом (рис. 3.1).
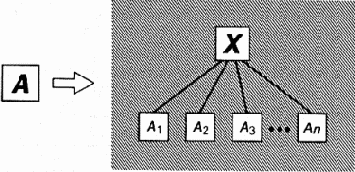
Рис. 3.1. Метасистемный переход
Это понятие будет играть решающую роль в последующем изложении. Метасистемный переход создает высший уровень организации — метауровень по отношению к уровню организации интегрируемых подсистем. С точки зрения функциональной метасистемный переход состоит в том, что деятельность, являющаяся управляющей на низшем этапе, становится управляемой на высшем этапе и появляется качественно новый (высший) вид деятельности, заключающийся в управлении деятельностью. Редупликация и отбор приводят к созданию необходимых структур. Первый метасистемный переход, который мы усматриваем в истории животных, это возникновение движения. Интегрируемыми подсистемами являются части клетки, обеспечивающие обмен веществ и размножение. Положение этих частей в пространстве до поры до времени случайно, неуправляемо.
Но вот появляются органы, соединяющие остальные части клетки и приводящие их в движение: клеточная мембрана, реснички, жгутики. Происходит метасистемный переход, который можно определить формулой
Управление положением = Движение.
На этом этапе движение неуправляемо, никак не коррелировано с движением внешней среды. Сделать его управляемым — следующая задача природы. Управлять движением — значит сделать его определенной функцией состояния среды. Так возникает раздражимость — изменение состояния каких-то участков клетки под действием внешних факторов и распространение этого изменения на другие участки, в частности обеспечивающие движение. Итак, формула метасистемного перехода от второго к третьему этапу такова:
Управление движением = Раздражимость.
Интеграция клетки с образованием многоклеточного организма также является переходом от системы к метасистеме. Однако этот переход касается исключительно структурного аспекта и неописуем в функциональных терминах. С точки зрения функциональной неважно в конце концов, происходят ли размножение и интеграция в какой-то части организма или организмы интегрируются целиком. Это, так сказать, вопрос технический. Раздражимость появляется уже у одноклеточных организмов, но полностью проявляет свои возможности после интеграции клеток.
Здесь необходимо указать на одну важную черту метасистемного перехода. Когда интегрируемые подсистемы объединяются в метасистему, то вследствие разделения функций между ними происходит их специализация, т. е. приспособление к определенной частной деятельности и утрата способности к другим видам деятельности. Специализация особенно отчетливо проявляется при интеграции целых организмов. Каждая интегрируемая подсистема содержит в этом случае много «лишнего» того, что было необходимо ей для самостоятельной жизни, но не нужно в сообществе, ибо соответствующие функции выполняются другими подсистемами. Так, в многоклеточном организме появляются специализированные мышечные и нервные клетки.
Вообще надо отметить, что интеграция подсистем отнюдь не является концом их эволюционирования.
Нельзя представить дело таким образом, что системы A1, A2, A3, … размножаются в больших количествах, после чего «над ними» вдруг возникает управляющее устройство X. Напротив, зачатки системы управления образуются, когда число подсистем Ai
невелико — всего несколько штук. Только при таком условии, как мы видели выше, может работать метод проб и ошибок. Уже после того, как наметилась управляющая подсистема X, происходит массовая редупликация подсистем Ai, в процессе которой совершенствуются как Ai, так и X.
Возникновение структуры управления подсистемами Ai, не завершает, а вызывает бурный рост числа подсистем Ai, и предшествует ему, ибо при этом размножение Ai, становится нужным для организма. Носитель определенного уровня организации разрастается лишь после того, как начинает образовываться новый, более высокий уровень. Эту черту можно назвать законом разрастания предпоследнего уровня. Поэтому и при феноменологическом функциональном описании метасистемный переход проявляется не тотчас же вслед за закладкой нового уровня, а несколько позже, когда предпоследний уровень «войдет в силу». Метасистемный переход всегда затрагивает два уровня организации.
Продолжим наш обзор этапов эволюции. Применим принцип метасистемного перехода к уровню раздражимости. На этом уровне возбуждение каких-то участков одноклеточного организма или специализированной нервной клетки в многоклеточном организме происходит непосредственно внешней средой и это возбуждение непосредственно (один к одному) вызывает возбуждение мышечной активности. Что может означать управление раздражимостью? Очевидно, создание нервной сети, элементы которой, в частности эффекторы, возбуждаются не прямо внешней средой, а через посредство сложной управляющей системы. Это тот этап эволюции, который мы связали с понятием сложного рефлекса. Особенно отчетливо виден факт управления раздражимостью на этом этапе в том, что при наличии цели возбуждение эффекторов зависит не только от состояния внешней среды, но и от этой цели, т.е. от состояния каких-то внутренних нейронов сети. Итак, формула этого метасистемного перехода (от третьего к четвертому этапу):
Управление раздражимостью = Сложный рефлекс.
Что же дальше?
Метасистемный переход к языковой деятельности
Первобытная фаза — это фаза мышления, непосредственно следующая за возникновением языка и характеризующаяся тем, что языковая деятельность еще не стала своим собственным объектом. Переход к фазе современного мышления — это метасистемный переход, состоящий в том, что возникает языковая деятельность, направленная на языковую деятельность. Язык первобытного человека — это язык первого уровня, язык современного человека — язык второго уровня, включающий, в частности, грамматику и логику. Однако переход к современному мышлению не сводится только к метасистемному переходу в языке, если рассматривать язык статически, как некую возможность или способ деятельности. Он включает метасистемный переход в реальной языковой деятельности как общественно значимой норме поведения. При переходе к фазе современного мышления становится общепринятым не только думать что-то о чем-то, но и задавать себе вопросы: а почему я так думаю? Можно ли думать иначе? К каким последствиям приводят те или иные мысли? Коротко говоря, отличие современного мышления от первобытного заключается в том, что оно является мышлением критическим, в то время как первобытное мышление можно назвать докритическим. Критическое мышление так прочно вошло в норму, что воспринимается как нечто само собой разумеющееся, единственно возможное. Правда, нам случается говорить, что то или иное лицо мыслит «некритически», но сам этот термин показывает, что не критическое мышление является не нормой, а отклонением от нормы. Как правило, не критичность мышления рассматривается как недостаток. Тогда стараются чем-то объяснить его: влиянием эмоций, нежеланием прийти к определенным выводам и т. п. Не критичность по отношению к некоторым утверждениям (догматам) может оправдываться особым (священным) происхождением этих утверждений. В основном же потоке наше мышление продолжает оставаться критическим. Это не значит, что оно всегда оригинально и нешаблонно. Но и когда мы мыслим по шаблону, мы, тем не менее, мыслим критически, ибо таков сам шаблон: он включает языковую деятельность, направленную на языковую деятельность, он учит отделять имя от значения и помнить о произвольности связи между ними, он учит думать: «А почему я так говорю и думаю?» И мы не только сами пользуемся этим шаблоном, но пользуемся также результатами использования этого шаблона предшествующими поколениями, внесшими вклад в создание нашей современной культуры.
Иначе обстоит дело в первобытном обществе. Здесь общественной нормой мышления является отношение к словам, представлениям и регламентациям своей культуры, как к чему-то безусловно данному, абсолютному, не отделимому от других элементов реальности, ибо связь между языком и действительностью еще не стала объектом мысли. Это очень существенное отличие от современного образа мышления. Мы рассмотрим первобытное мышление более детально и покажем, что из этой особенности — докритичности — вытекают его основные наблюдаемые черты.
Ниже в этой главе мы пользуемся данными, взятыми из книги Л. Леви-Брюля1. Эта книга интересна тем, что в ней собран большой материал о первобытных культурах, убедительно показывающий отличие первобытного мышления от современного. Что касается концепции Леви-Брюля, то как ее положительную черту следует отметить, что мышление отдельных членов первобытного (в действительности, конечно, не только первобытного, но этого Леви-Брюль почему-то не замечает) общества описывается им как регулируемое коллективными представлениями данной культуры. Заслугой Леви-Брюля является также указание на то, что коллективные представления в первобытном обществе отличаются от наших, поэтому объяснение мышления первобытного человека путем подстановки (часто неосознанной) на его место современного человека совершенно неправомерно. В остальном концепция Леви-Брюля довольно бессодержательна. Он описывает первобытное мышление как «пралогическое», «мистически ориентированное» и «управляемое законом партиципации (сопричастия)». Эти понятия остаются весьма туманными и ничего не прибавляют к собранному материалу. Сочувствие вызывает только сам термин «пралогическое мышление», перекликающийся с нашим определением первобытного мышления как докритического.
Метасистемный переход в языке
Язык возникает в результате кодирования явлений действительности языковыми объектами. Но, возникнув, он сам становится явлением действительности. Языковые объекты становятся важнейшими элементами общественной деятельности, они входят в жизнь человека подобно орудиям труда и домашней утвари. И подобно тому, как для изготовления и усовершенствования орудий труда человек создает новые орудия труда, он создает новые языковые объекты для описания действительности, которая уже содержит языковые объекты. Происходит метасистемный переход в рамках системы «язык». Так как новые языковые объекты в свою очередь являются элементами действительности и могут стать объектом кодирования, метасистемный переход может повторяться неограниченное число раз. Подобно другим кибернетическим системам, которые мы рассматривали в этой книге, язык является частью развивающейся Вселенной и развивается сам. И подобно другим системам язык, а вместе с ним и мышление претерпевают качественные изменения путем метасистемных переходов различного масштаба, т. е. захватывающих более или менее крупные подсистемы системы «язык».
При всем различии в физико-химическом отношении, которое существует между языковой системой и нейронной системой, легко видеть, что функционально метасистемные переходы в языке являются естественным продолжением метасистемных переходов в нейронных структурах, служа для создания более совершенных моделей действительности. Для пояснения этой мысли мы снова вернемся к схеме на рис. 7.4. Будем ее рассматривать как схему устройства обработки информации, поступающей от светящегося экрана, а, следовательно, и как частичную (и грубую) модель устройства мозга. На схеме мы видим классификаторы, соответствующие понятиям «пятно», «контур», «внутри» и «войти в». Эти понятия лежат на различных уровнях иерархии, и число уровней, в принципе, не ограничено. Но поставим вопрос: не возможен ли метасистемный переход более крупного масштаба, который можно изобразить не как добавление нового уровня на рис. 7.4, а вообще как выход из плоскости чертежа, создание новой плоскости?
Если сопоставлять нашу искусственную систему реальным биологическим системам, то она соответствует нервной сети с жестко фиксированной иерархией понятий. Это этап сложного рефлекса. Выйти в новую плоскость значило бы перейти к этапу ассоциирования, когда становится управляемой система связей между классификаторами.
Понятия, фигурирующие на рис. 7.4, взяты из языка. Существуют ли в языке понятия, которые «выходят из плоскости» рис. 7.4? Существуют. О понятии «внутри» мы можем сказать, что оно является примером пространственного отношения между объектами. Другими примерами пространственных отношений являются понятия «соприкасается», «пересекается», «между» и т. п. Схему на рис. 7.4 можно было бы дополнить классификаторами, распознающими эти понятия. Ну а само понятие «пространственное отношение»? Оно-то и является искомым метапонятием по отношению к понятиям «внутри», «между» и т. п., оно относится к ним как имя к значению. Если бы мы задумали воплотить понятие «пространственное отношение» в виде какого-то устройства, дополняющего устройства на рис. 7.4, то оно явно должно было бы образовать метасистему по отношению к классификаторам «внутри», «между» и пр. Задача, которую оно могло бы выполнять, это модификация структуры или работы упомянутых классификаторов, или создание новых классификаторов, распознающих какие-то новые, до тех пор не распознаваемые пространственные отношения. А в самом языке с какой целью появляется понятие «пространственное отношение»? Да с такой же! Для лучшего понимания того, как работает языковая система, для ее модификации и создания новых понятий. Метасистемный переход в развитии языка выполняет ту же роль, что и в развитии нейронных структур.
Мир глазами лягушки
Для исследования иерархии классификаторов и понятий, относящихся к зрительному восприятию у животных, чрезвычайно интересна работа четырех ученых из Массачусетского технологического института (Дж.Летвин и др.) «Что сообщает глаз лягушки мозгу лягушки»3. Лягушка была избрана авторами в качестве подопытного животного потому, что ее зрительный аппарат обладает некоторыми качествами простоты, которые делают его удобным для изучения. Прежде всего, сетчатка глаза лягушки однородна; она не имеет в отличие от глаза человека области с повышенной чувствительностью, на которую нужно проектировать наиболее важную часть изображения. Поэтому и взгляд лягушки неподвижен, она не следит взглядом за двигающимся предметом, как это делаем мы. С другой стороны, если лягушка качается, сидя на листе кувшинки, ее глаза совершают такие движения, которые компенсируют качание, так что изображение внешнего мира на сетчатке остается неподвижным. Информация от сетчатки передается по зрительному нерву к так называемому зрительному бугру мозга. Этим лягушка также отличается от человека в сторону простоты, так как у человека есть два канала передачи информации от сетчатки к мозгу.
Зрение играет большую роль в жизни лягушки: с его помощью она охотится и спасается от врагов. Исследование поведения лягушки показывает, что она отличает добычу от врага по размерам и состоянию движения. Очень интересно, что движение играет здесь решающую роль. Завидев маленький (размеров насекомого или червя) движущийся предмет, лягушка прыгает и схватывает его. Лягушку можно обмануть, раскачивая на ниточке маленький несъедобный предмет. Но на неподвижного червяка или насекомое лягушка не обращает ни малейшего внимания, и она может умереть с голоду среди обилия пищи, если эта пища неподвижна. Большие движущиеся предметы лягушка считает врагами и спасается от них бегством.
Сетчатка глаза лягушки, как и других позвоночных, имеет три слоя нервных клеток. Верхний (самый внешний) слой образуют светочувствительные рецепторы — палочки и колбочки.
Затем идет слой ассоциативных нейронов нескольких типов. Одни из них (так называемые биполярные
клетки) дают преимущественно вертикальные аксоны, по которым возбуждение передается в более глубокие слои. Другие (горизонтальные, или амакринные
клетки) связывают нейроны, расположенные на одном уровне. Последний по глубине залегания — третий слой — образуют так называемые ганглиозные клетки. Их дендриты получают информацию от клеток второго слоя, а аксоны представляют собой длинные волокна, которые сплетаются в жгут — зрительный нерв, соединяющий сетчатку с мозгом. Эти аксоны ветвятся, входя в зрительный бугор мозга, и передают информацию дендритам мозговых нейронов.
Глаз лягушки имеет около миллиона рецепторов, около трех миллионов ассоциативных нейронов второго слоя и полмиллиона ганглиозных клеток. Такая структура сетчатки дает основание предположить, что анализ изображения начинается уже в глазу животного и изображение передается по зрительному нерву в терминах каких-то промежуточных понятий. Сетчатка как бы является вынесенной на периферию частью мозга. Это предположение подтверждается тем, что расположение на поверхности зрительного бугра точек входа нервных волокон (аксонов) совпадает с расположением соответствующих ганглиозных клеток на выходе сетчатки. И это несмотря на то, что на протяжении зрительного нерва волокна многократно переплетаются друг с другом и меняют свое положение на срезе нерва. Наконец, к тому же заключению приводят и данные эмбриологии о развитии сетчатки.
В описываемых опытах в зрительный нерв лягушки вводился тонкий платиновый электрод, что позволяло регистрировать возбуждение отдельных ганглиозных клеток. Лягушка помещалась в центр алюминиевой полусферы, имеющей (изнутри) матово-серый цвет. По внутренней поверхности полусферы могли перемещаться различные темные предметы — прямоугольники, диски и т. п., поддерживаемые с помощью магнита, расположенного с внешней стороны полусферы.
Результаты экспериментов мы можем суммировать следующим образом.
Каждая ганглиозная клетка имеет определенное рецептивное поле, т. е. участок сетчатки (множество рецепторов), с которого она собирает информацию. Состояние рецепторов вне рецептивного поля никак не влияет на состояние ганглиозной клетки. Размеры рецептивных полей у клеток разного типа, если измерять их угловыми размерами соответствующей видимой области, варьируются от 2 до 15° в диаметре.
Ганглиозные клетки делятся на четыре типа в зависимости от того, какой процесс в своем рецептивном поле они регистрируют. Эти типы следующие:
Детекторы длительно сохраняющегося контраста. Эти клетки не реагируют на включение или выключение общего освещения. Но если в рецептивном поле появляется край объекта, более темного или более светлого, чем фон, цвета, то клетка сразу же начинает генерировать импульсы.
Детекторы выпуклых краев. Эти клетки возбуждаются в том случае, если в рецептивном поле появляется маленький (не более 3°) выпуклый объект. Максимальное возбуждение (частота импульсов) достигается, когда диаметр объекта составляет примерно половину диаметра рецептивного поля. На прямой край объекта клетка не реагирует.
Детекторы движущихся краев. Их рецептивное поле обладает шириной примерно 12°. Клетка реагирует на любой различимый край объекта, более темного или более светлого, чем фон, цвета; но только при условии, что он движется. Если через поле плавно перемещается предмет шириной более 5°, то возникают две реакции: на передний и на задний край.
Детекторы затемнения поля. Они посылают серию импульсов, если внезапно уменьшается общая освещенность рецептивного поля.
Чрезвычайно интересно, как расположены окончания зрительных волокон в зрительном бугре мозга. Мы уже говорили, что в плане это расположение совпадает с расположением соответствующих ганглиозных клеток в сетчатке. Но, кроме того, оказывается, что окончания волокон каждого типа находятся в зрительном бугре на определенной глубине, так что в мозгу лягушки имеется четыре слоя нейронов, воспринимающих зрительную информацию, и каждый слой как бы получает оттиск сетчатки, но в определенном аспекте соответственно одному из четырех типов ганглиозных клеток.Эти слои и являются датчиками информации для высших отделов мозга.
Опыты, подобные описанным, довольно сложны, и по поводу их интерпретации иногда возникают споры. Детали описанной системы могут измениться или получить другое толкование. Тем не менее общий характер системы понятий первого уровня установлен, по-видимому, достаточно твердо. Мы видим переход от точечного описания к локальному, учитывающему непрерывную структуру изображения. Ганглиозные клетки служат распознавателями таких первичных понятий, как край, выпуклость, движение, отнесенных к определенной области видимого мира.
Моделирование
До сих пор, говоря об ассоциациях представлений, мы полностью игнорировали их динамический, временной аспект, т. е. рассматривали связываемые представления как статические и не имеющие никакой координаты во времени. Между тем идея времени может активно входить в наши представления. Мы можем представить себе фигуры, движущиеся и меняющиеся с определенной скоростью, можем мысленно продолжить наблюдаемый процесс. По дороге катится колесо. Вы закрываете глаза на пару секунд и представляете движение колеса. Открыв глаза, вы видите его на том самом месте, где и ожидали. Это, конечно, результат ассоциации представлений, но такой ассоциации или, вернее, таких представлений, которые органически связаны с течением времени. Положение x колеса в момент времени t ассоциируется с положением х1 в момент времени t + ?t, а также с положением х2 в момент времени t + 2?t и т. д. Каждое из этих представлений включает в себя представление о времени, к которому оно относится. Каков механизм этого включения, мы не знаем и в соответствии с нашим подходом не будем строить на этот счет никаких гипотез. Заметим только, что ничего особенно удивительного в таком включении нет. Хорошо известно, что в организме есть свой датчик времени — «внутренние часы».
Ассоциация представлений, имеющих временную координату, дает вам возможность предвидеть в своем воображении будущие ситуации. Мы установили наличие таких представлений, опираясь на внутренний, субъективный опыт. Но из того факта, что животные также обнаруживают способность предвидения (посмотрите, как ловит собака кусок сахара), мы заключаем, что их представления могут обладать временной координатой.
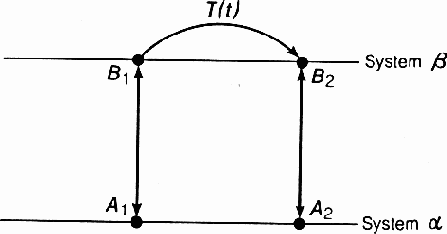
Рис. 3.8. Схема моделирования
Говоря языком кибернетики, связывание представлений, включающих временную координату, и вытекающая отсюда способность предвидеть будущее есть не что иное, как моделирование, построение модели окружающей среды.
Дадим общее понятие модели. Рассмотрим две системы ? и ?. Допустим, что каждому состоянию Ai, системы ? мы можем каким-то образом сопоставить одно определенное состояние Bi, системы ? (рис. 3.8).
Обратное соответствие не обязательно должно быть однозначным, т. е. одному состоянию ? может соответствовать множество состояний ?. Так как обобщенное состояние согласно нашему определению есть множество состояний, можно характеризовать это положение как взаимно однозначное соответствие состоянии системы ? обобщенным состояниям системы ?. Это необходимо, но не достаточно, чтобы считать систему ? моделью системы ?. Должно еще существовать такое преобразование T(t) системы ?, зависящее от времени t, которое моделирует естественное течение времени в системе ?. Это означает следующее. Пусть первоначально система ? находится в обобщенном состоянии A1, которому соответствует состояние Bi, системы ?. Пусть по прошествии времени t состояние системы ? становится A2. Тогда преобразование T(t) должно переводить систему ? в состояние B2, соответствующее обобщенному состоянию A2. Если это условие выполнено, мы называем систему ? моделью системы ?.
Преобразование T(t) может, в частности, заключаться просто в том, что мы предоставляем системе ? самой по себе менять свое состояние со временем. Такие модели называют моделями в естественном масштабе времени.
...Осаждающие сделали подкоп под крепостную стену и заложили в него несколько бочек с порохом. Рядом горит свеча, от основания которой начинается пороховая дорожка к бочкам. Когда свеча догорит, будет взрыв. Точно такая же свеча, зажженная в то же время, горит на столе в палатке предводителя осаждающих. Эта свеча служит для него моделью первой. Зная, сколько времени осталось до взрыва, он отдает последние распоряжения... Свирепые лица склонились над столом, волосатые руки сжимают оружие. Свеча догорает. Страшный взрыв сотрясает воздух. Модель не подвела...
Изображение на экране телевизора, когда идет трансляция футбольного матча, можно тоже формально считать моделью футбольного поля и трибун стадиона. Действительно, все условия соблюдены. Однако чувствуется большое различие между случаем двух свечей и случаем трансляции матча.
В чем оно состоит? В различии информационных связей между системами ? и ?. Любое изображение ? объекта ? является в широком смысле слова его моделью. Но от ? к ? существует непрерывный поток информации, и только благодаря этому потоку сохраняется соответствие между состояниями ? и ?. Имея информационный доступ к ?, мы фактически имеем доступ к ?. Система ? служит лишь фазой передачи информации от ?. Совсем другое дело в случае двух свечей. Свеча ? горит с такой же скоростью, как свеча ?, но независимо от нее. Предводитель осаждающих не имеет доступа к свече ? и не может получить никакой реальной информации о ее состоянии. Путем моделирования он компенсирует этот недостаток получением эквивалентной информации. Система ? играет здесь принципиально другую, более существенную роль. С ее помощью как бы преодолевается пространственный барьер, причем без установления каких-либо новых информационных каналов.
Еще более важен случай, когда модель помогает преодолевать не пространственный, а временной барьер. Информационного канала в будущее, увы, не проложишь. А модель позволяет нам действовать так, как будто такой канал есть. Для этого надо только, чтобы выполнение преобразования T(t) над моделью занимало меньше времени, чем само время t. Можно было бы привести много примеров использования таких моделей в жизни современного человека, однако вряд ли в этом есть необходимость. Вернемся еще раз к ассоциациям представлений.
Мы видели, что ассоциации статических представлений отражают наличие пространственных корреляций, взаимосвязей в окружающей среде. Точно так же ассоциации динамических представлений — модели, создаваемые мозгом — отражают динамические временные корреляции, свойственные внешней среде. Ситуация х через время t вызывает (или может вызвать) ситуацию Y — вот общая формула таких корреляций, и эти корреляции запечатлеваются в мозгу в виде соответствующих ассоциаций.
Мозг как «черный ящик»
Сначала попытаемся элементам языка найти непосредственные корреляты в деятельности мозга.
Первое понятие, которое мы ввели при описании языка логики — это высказывания. Что можно ему сопоставить? Напрашивается ответ: ассоциацию представлений. Действительно, язык, как и мозг, — система, служащая для создания моделей действительности. В случае мозга основной самостоятельной единицей, которая может действовать как модель, является ассоциация представлений, в случае языка — высказывание.
Теперь возникает искушение сопоставить объекту представление. На первый взгляд это создает полную и стройную интерпретацию: объект соответствует представлению, отношение между объектами, т. е. высказывание, соответствует отношению между представлениями — ассоциации. Можно взять пример ассоциации «в лесу — волки», который мы приводили в главе 4, и истолковать его следующим образом: «лес» и «волки» — это объекты и в то же время представления, «в лесу — волки» — это высказывание и в то же время ассоциация.
Однако внимательный анализ показывает, что эта интерпретация — большая натяжка, это искусственное внесение языковой структуры в сферу представлений, которая на самом деле такой структурой не обладает. Начать с того, что ассоциация представлений — это тоже представление. Предложению «в лесу — волки» точно так же можно сопоставить представление, как существительным «лес» и «волки». Напомним, что ассоциация между представлениями S1 и S2
есть новое синтетическое представление U (см. рис. 3.7). Верно, что ассоциация представлений есть модель действительности. Но если понимать термин «модель» в широком смысле как некий коррелят действительности, то и любое представление есть модель. Если же понимать модель в узком смысле как коррелят действительности, позволяющий делать предсказания относительно будущих состояний, то не всякая ассоциация будет моделью, а лишь такая, которая отражает временной аспект действительности. Процесс ассоциирования важен потому, что приводит к созданию новой модели, которой ранее не было.
Этот процесс допускает вполне строгое логическое определение и может быть обнаружен в опыте подобно тому, как процесс образования системы из подсистем легко определим и обнаружим. Но нельзя определить различия между ассоциацией представлений и представлением, как нельзя установить критерий, по которому отличать системы от подсистем.
Итак, высказывание вызывает представление и объект вызывает представление и наша стройная система рассыпается. Представление оказывается слишком широким и неопределенным понятием, чтобы положить его в основу при изучении семантики языка. О представлении мы знаем только, что оно является обобщенным состоянием мозга, а о структуре мозга мы не знаем почти ничего.
В главе 4 мы определили язык как совокупность объектов Li, каждый из которых является еименм некоторого объекта Ri, называемого его значением. Относительно объекта Ri мы сказали только, что это какие-то явления действительности. Теперь пришло время заниматься уточнением вопроса, что это за явления, т. е. какова семантика естественного языка.
В простейших примерах, которые обычно приводятся для иллюстрации Li
— Ri и которые мы приводили выше (слово «лев» — животное лев и т. п.), объект Ri — это представление об определенном предмете. Вообще язык возникает в результате ассоциации между языковыми и прочими представлениями, поэтому естественно попытаться определить семантику языка через те представления, которые возникают в процессе языковой деятельности. Можно сказать, что значение языкового объекта — это то представление, которое оно вызывает, т. е. фактически то изменение состояния мозга, которое происходит, когда в сознании появляется представление о языковом объекте. Это определение вполне верное, но, увы, не продуктивное, ибо состояния мозга как объективная реальность непосредственно нам недоступны и мы судим о них лишь по их проявлению в действиях человека.
Поэтому встанем на другой путь. Будем рассматривать мозг как «черный ящик», т. е., не пытаясь постичь его устройство, исследовать только наблюдаемые проявления его деятельности.
Нас интересует семантика языка, т. е. связь (ассоциации) между языковыми представлениями и всеми прочими представлениями (рис. 7.2). Но, поскольку представления находятся внутри «черного ящика», будем опираться только на соответствующие им входные данные, т. е. языковые объекты, и всю остальную часть действительности, которую мы будем для краткости называть неязыковой. Таков вход «черного ящика». Его выход, очевидно, это наблюдаемые действия человека.
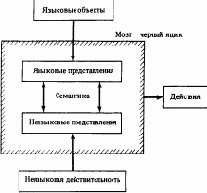
Рис. 7.2. Мозг как «черный ящик»
Так как система действий весьма сложна, мы не сдвинемся с места в попытках изучения семантики, если не выберем какой-то простой тип действия в качестве эталона. Очевидно, должно быть не менее двух вариантов действия, чтобы оно несло какую-то информацию. Пусть их будет ровно два. Назовем их первым и вторым эталонными действиями. Элементарный акт по изучению семантики оформим следующим образом. Человеку, воспринимающему определенную неязыковую действительность, будем предъявлять языковые объекты, а он пусть совершает в качестве реакции на предъявление одно из двух эталонных действий.
Мусорная куча представлений
Как мы уже указывали, не сам факт веры в существование невидимых вещей и влияний отличает первобытное мышление от современного, а содержание представлений и особенно его отношение к данным опыта. Мы верим в существование нейтронов, хотя никто не видел их и никогда не увидит. Но мы знаем, что все слова, которые мы произносим, имеют смысл лишь постольку, поскольку они в своей совокупности успешно описывают наблюдаемые явления и помогают их предсказывать. Как только они перестают выполнять эту роль из-за новых данных опыта или из-за перестройки системы словоупотребления (теории), мы их безжалостно отбрасываем. Так случилось, например, с теплородом или эфиром. Еще раньше исчезли из языка и мышления всевозможные воображаемые существа и предметы, столь типичные для мышления наших предков. В первобытном мышлении нас возмущает не допущение существования духов, а то, что это допущение — конечно, вместе с какими-то допущениями о свойствах и повадках духов — решительно ничего не объясняет, а часто просто противоречит опыту. Приведем несколько типичных свидетельств исследователей. На Никобарских островах
туземцы во всех селениях совершили церемонию, называемую «танангла» (т. е. помощь или защита). Церемония эта была призвана предотвратить болезнь, появлявшуюся с северо-западным муссоном. Бедные никобарцы! Они делают это из года в год и все без результата! (Соломон).
Казалось бы, что тяжелой раны от удара копьем вполне достаточно, чтобы объяснить смерть раненого. Тем не менее, если раненый умирает, абипоны верят, будто не оружие убило раненого, а злодейское искусство какого-то колдуна... Они убеждены, что колдун умрет в свою очередь в наказание за убийство их сородича, если только сейчас же после смерти покойника вырвать у него язык и сердце, зажарить их на огне и отдать на съедение собакам. Хотя уже много сердец и языков было съедено собаками и никто ни разу не видел, чтобы непосредственно после этого умер какой-нибудь колдун, абипоны свято сохраняют привязанность к обычаю своих предков и продолжают вырывать язык и сердце у детей и взрослых обоего пола, как только они испускают дух (М.Добрицгофер).
Так как первобытный человек не умеет делать свои представления объектом анализа, они образуют своего рода мусорную кучу. Пополняется эта куча легко, но вот расчисткой ее никто не занимается. Бессмысленных слов для первобытного человека нет и быть не может. Если он не понимает слова, то оно пугает, как пугает незнакомое животное, или оружие, или природное явление. Мнение, возникшее благодаря случайному стечению обстоятельств, сохраняется из поколения в поколение, не имея под собой никакого реального основания. Объяснение какого-либо явления может быть совершенно произвольным и, тем не менее, полностью удовлетворять первобытного человека. Критическое мышление рассматривает каждое объяснение (языковую модель действительности) наряду с другими, конкурирующими объяснениями (моделями), и оно не удовлетворится, пока не будет показано, чем данное объяснение лучше, чем конкурирующее. Это называют в логике законом достаточного основания. Докритическому мышлению закон достаточного основания абсолютно чужд. Здесь ярче всего виден метасистемный переход, отделяющий современное мышление от первобытного.
Благодаря этой особенности вера первобытного человека в действенность магии, заклинания, колдовство и т. п. непоколебима. Его «теория» дает объяснение (часто даже не одно, а несколько!) всему, что происходит вокруг него. Оценить же критически свою теорию или хотя бы отдельные ее части он еще не может. Один дикарь обзавелся фетишем, который должен был сделать его неуязвимым, рассказывает Т.Боудич. Он решил испытать его и получил пулю в руку, которая сломала ему кость. Колдун объяснил это обстоятельство к всеобщему удовлетворению, заявив, что оскорбленный фетиш только что открыл ему причину того, что произошло: этот молодой человек имел половые сношения со своей женой в запретный день. Раненый признался, что это правда, и его соплеменники только укрепились в своей вере. Подобных примеров можно привести несчетное множество.
Мышление человека и животных
Иногда говорят, что мышление человека отличается от мышления животных тем, что человек может мыслить в абстрактных понятиях, в то время как животным абстрактные понятия недоступны, а доступны лишь некоторые конкретные понятия. Если термин «абстрактное» понимать как отвлеченное от несущественных признаков (а именно такое понимание является нормой и принято, в частности, в настоящей книге), то это утверждение не выдерживает ни малейшей критики. Мы видели, что решающее отличие мышления человека состоит в наличии управления ассоциациями, которое в первую очередь проявляется как способность к воображению. Что же касается различия в понятиях, то оно во всяком случае не сводится к противопоставлению: абстрактное-конкретное. Всякое понятие абстрактно. Понятие кошка для собаки является абстрактным, ибо содержит, например, отвлечение от расцветки кошки (несущественный признак). Если измерять умственные способности степенью абстрактности понятий, то лягушка окажется одним из самых умных животных, ибо она мыслит с помощью всего-навсего двух, но зато чрезвычайно абстрактных понятий: «нечто маленькое и быстро движущееся» и «нечто большое, темное и не очень быстро движущееся». Как видите, в нашем языке даже не оказалось специальных терминов для этих понятий.
Действительно глубокое отличие в понятийном багаже высших животных и человека состоит в том, что животным недоступны понятия-конструкты, ибо эти понятия предполагают способность к языковой деятельности. Не абстрактные понятия, а понятия-конструкты составляют специфику человеческого мышления. В частичное оправдание приведенного выше суждения надо заметить, что «абстрактными понятиями» часто называют именно понятия-конструкты и говорят о степени абстрактности, когда на самом деле надо было бы говорить о степени «конструктности». Правда, понятие числа образуется путем абстракции, отправляясь от конкретных чисел, а понятие пространственного отношения – отправляясь от конкретных отношений. Но специфику здесь составляет не сам процесс абстракции (он, как мы видели, появился на самых ранних этапах кибернетического периода жизни), а то, что в процессе абстракции существеннейшим образом участвуют языковые объекты. Здесь главное — не абстракция, а конструкция, создание иерархической системы понятий, фиксированных материалом языка. Абстракция без конструкции приводит просто к потере содержания, к таким понятиям, как «нечто» и «некоторый».
1 Цит. по кн.: Новое в лингвистике. М., 1960. Вып.1.
2 См. там же статьи Б. Уорфа.
Надежность дискретных систем
Почему же, когда необходимо выполнять сложные функции, дискретные системы оказываются предпочтительнее, чем непрерывные? Потому что они отличаются более высокой надежностью. В кибернетическом устройстве, основанном на принципе дискретных состояний, каждая элементарная подсистема может находиться лишь в небольшом числе возможных состояний, поэтому она, как правило, игнорирует малые отклонения от нормы различных физических параметров системы, восстанавливая «в первозданной чистоте» одно из своих допустимых состояний. В то же время в непрерывной системе малые возмущения непрерывно накапливаются и, если система слишком сложна, она перестает правильно работать. Конечно, и в дискретной системе всегда существует возможность сбоя, ибо небольшие изменения физических параметров все-таки приводят к конечной вероятности перехода подсистемы в «неправильное» состояние. И все-таки преимущество, бесспорно, на стороне дискретных систем. Покажем это на следующем простом примере.
Пусть нам надо передать сообщение с помощью электрического провода на расстояние, скажем, 100 км. И пусть через каждый километр провода мы имеем возможность поставить автоматическую станцию, которая будет усиливать сигнал до той мощности, которую он имеет на предыдущей станции, и — если нужно — как-то преобразовывать его (рис. 1.1).
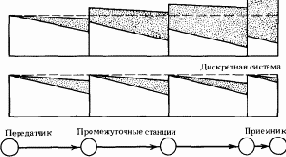
Рис. 1.1. Передача сигнала в непрерывной и дискретной системах. Затенением показана область неопределенности сигнала
Допустим, что максимальная величина сигнала, который позволяет послать наша аппаратура, составляет 1 В и что среднеквадратичное искажение сигнала при передаче от станции к станции (помеха) равно 0,1 В.
Рассмотрим сначала непрерывный способ передачи информации. Тогда содержанием сообщения будет величина напряжения, приложенного к проводу у его начала. Величина напряжения на другом конце провода — принятое сообщение — будет из-за помех отличаться от начального напряжения. Как велико будет это отличие? Считая помехи на различных участках линии независимыми, мы находим, что после прохождения ста станций среднеквадратичная величина помехи составит 1 В (складываются средние квадраты помех).
Таким образом, помеха в среднем равна максимальному сигналу, поэтому ясно, что никакой полезной информации мы фактически не получим. Значение принятого напряжения может совпадать со значением переданного напряжения разве что случайно. Если, например, нас устраивает точность в 0,1 В, то вероятность такого совпадения равна примерно 1/10.
Теперь рассмотрим дискретный способ передачи. Определим два «осмысленных» состояния начального участка провода: когда приложенное напряжение равно нулю и когда оно максимально (1 В). На промежуточных станциях установим автоматические устройства, которые в одном случае, если принято напряжение меньше 0,5 В, передают дальше нулевое напряжение, а если оно больше 0,5 В, посылают нормальный сигнал в 1 В. Следовательно, в данном случае за один раз (одним сигналом) передается информация вида «да» или «нет» (такое количество информации — единица информации — называется 1 бит). Какова вероятность получения правильной информации? Она сильно зависит от закона распределения вероятности для величины помехи. Как правило, помехи подчиняются так называемому нормальному закону. Приняв этот закон, можно найти, что вероятность ошибки при передаче от предыдущей станции к следующей (равная вероятности того, что помеха превысит 0,5 В) равна 0,25×10-6. Следовательно, вероятность ошибки при передаче на всю длину линии есть 0,25×10-4. Чтобы передать то же сообщение, что и в предыдущем случае, т. е. значение с точностью до 0,1 некоторой величины, лежащей в пределах от 0 до 1, нам достаточно послать четыре сигнала вида «да» или «нет». Вероятность того, что хотя бы в одном из сигналов будет допущена ошибка, равна 10-4. Итак, полная вероятность ошибки при дискретном способе составляет 0,01% против 90% при непрерывном способе.
Наглядные и знаковые модели
Итак, у электрона не существует траектории. Самое большое, что можно сказать об электроне, — это указать его волновую функцию, квадрат которой даст нам вероятность обнаружения электрона вблизи той или иной точки пространства. В то же время мы говорим, что электрон — материальная частица определенных (и очень маленьких) размеров. Смешение этих двух представлений, которого потребовали опытные факты, оказалось делом очень нелегким, и до сих пор все еще находятся люди, которые отвергают обычную интерпретацию квантовой механики (принятую вслед за школой Бора подавляющим большинством физиков) и желают во что бы то ни стало вернуть квантовым частицам их траекторию. Откуда же такая настойчивость? Ведь экспроприация у электронов цвета прошла совершенно безболезненно, а с логической точки зрения признание неприменимости к электрону понятия траектории принципиально ничем не отличается от признания неприменимости понятия цвета. Различие здесь в том, что при отказе от понятия цвета мы проявляем известную долю лицемерия. Мы говорим, что у электрона нет цвета, а сами представляем его в виде этакого серенького (или блестящего — это дело вкуса) шарика. Отсутствие цвета мы заменяем на произвольный цвет, и это нисколько не мешает использованию нашей модели. По отношению к положению в пространстве этот фокус не проходит. Представление об электроне, который в каждый момент где-то находится, мешает пониманию квантовой механики и приходит в противоречие с опытными данными. Здесь мы вынуждены полностью отказаться от наглядно-геометрического представления о движении частицы. Это и вызывает болезненную реакцию. Мы настолько привыкли соединять пространственно-временную картину с истинной реальностью, с тем, что существует объективно и независимо от нас, что нам очень трудно поверить в объективную реальность, которая не укладывается в эти рамки. И мы снова и снова спрашиваем себя: но ведь если электрон не «размазан» в пространстве, то на самом деле он где-то должен находиться?
Нужна упорная работа мысли, чтобы признать и прочувствовать бессмысленность этого вопроса.
Прежде всего, надо отдать себе отчет в том, что все наши знания и теории суть вторичные модели действительности, т. е. модели первичных моделей, каковыми являются данные чувственного опыта. Эти данные несут на себе неизгладимый отпечаток устройства нашей нервной системы, а так как пространственно-временные понятия заложены в самых нижних этажах нервной системы, все наши ощущения и представления, все продукты нашего воображения не могут выйти за рамки пространственно-временных картин. Тем не менее, эти рамки можно до известной степени расширить. Но это надо делать не путем иллюзорного движения «вниз» к объективной действительности, «какая она есть независимо от наших органов чувств», а путем движения «вверх», т. е. построения вторичных знаковых моделей действительности.
Разумеется, знаки теории сохраняют непрерывное пространственно-временное бытие, как и первичные данные опыта. Но в отношениях между теми и другими, т. е. в семантике теории, мы можем позволить себе значительную свободу, если будем руководствоваться логикой новых экспериментальных фактов, а не привычной пространственно-временной интуицией. И мы можем построить такую знаковую систему, которая в своем функционировании никак не связана наглядными представлениями, а подчинена единственно условию адекватного описания действительности. Квантовая механика и является такой системой. Квантовая частица в этой системе — не серенький или блестящий шарик и не геометрическая точка, а некоторое понятие, т. е. функциональный узел системы, который вместе с другими узлами обеспечивает описание и предвидение реальных опытных фактов: вспышек на экране, показаний приборов и т. д.
Возвратимся к вопросу о том, как «на самом деле» движется электрон. Мы видели, что из-за соотношения неопределенностей эксперимент в принципе не может дать на него ответа. Значит, в качестве «внешней части» физической модели действительности этот вопрос бессмыслен. Остается приписать ему чисто теоретический смысл. Но тогда он теряет непосредственную связь с наблюдаемыми явлениями и выражение «на самом деле» становится чистым надувательством! Всегда, когда мы выходим за пределы сферы восприятия и объявляем, что «на самом деле» имеет место то-то и то-то, мы движемся не вниз, а вверх — строим пирамиду языковых объектов и только вследствие обмана зрения нам кажется, что мы углубляемся в область, лежащую ниже чувственного опыта.
Выражаясь метафорически, плоскость, отделяющая чувственный опыт от реальности, является абсолютно непроницаемой и, пытаясь разглядеть, что под нею, мы видим лишь перевернутое отражение пирамиды теорий. Это не значит, что истинная реальность непознаваема и наши теории не являются ее моделями; надо помнить только, что все эти модели лежат по сию сторону чувственного опыта и бессмысленно сопоставлять отдельным элементам теорий призрачные «реальности» по ту сторону, как это делал, например, Платон. Представление об электроне как о маленьком шарике, движущемся по траектории, — такая же конструкция, как и сцепление знаков квантовой теории. Оно отличается только тем, что включает пространственно-временную картину, которой мы по привычке приписываем призрачную реальность с помощью бессмысленного в данном случае выражения «на самом деле».
Переход к сознательному построению знаковых моделей действительности, не опирающихся на какие-либо наглядные представления о физических объектах, — большое философское завоевание квантовой механики. Фактически физика стала знаковой моделью со времен Ньютона и именно своей знаковости она была обязана успехами (численные расчеты); однако наглядные представления присутствовали в качестве необходимого элемента. Теперь они стали необязательными, и это расширило класс возможных моделей. Те, кто хотят во что бы то ни стало вернуть наглядность, хотя видят, что теория лучше работает без нее, призывают на деле просто к сужению класса моделей. Вряд ли им это удастся. Их можно сравнить с тем чудаком, который в паровоз запрягал лошадь, ибо хотя он и видел, что повозка движется без лошади, признать такое положение нормальным было выше его сил. Знаковые модели — это паровоз, который вовсе не нуждается в лошади наглядных представлений для каждого из своих понятий.
Научное управление обществом
Социальный аспект управления наукой неотделим от проблемы управления обществом в целом. Наука и производство — повторим это еще раз — срастаются в единую систему. Неразрывно связаны с этой системой также политика и идеология. Наконец, оба аспекта метасистемного перехода, необходимого для развития науки, — метанаучный и социальный, тоже связаны неразрывно, и нет никакой надежды осуществить в полном объеме первый из них, не осуществив второго. Таким образом, мы имеем здесь единую, по существу, проблему — проблему научного управления обществом. И даже с точки зрения «чистой» науки эта проблема является проблемой номер один, не решив которую продвигаться вперед невозможно.
На начальных этапах развития науки у ученых было сравнительно благопристойное оправдание невмешательства в общественные дела. Можно было сказать, что наука сама по себе представляет одну из высших ценностей бытия и в дальнейшем она продемонстрирует свои удивительные возможности, а пока она в зародышевом состоянии и ей надо во что бы то ни стало предоставить покой и тепло для развития. Ученый мог сказать, подобно курице, сидящей на яйцах: «Делайте, что хотите, только оставьте меня в покое! Я высиживаю удивительного цыпленка. Это — главное».
В наше время такого сорта рассуждения представляли бы собой чистое лицемерие. Удивительный цыпленок вылупился из яйца и требует пищи. Теперь изолировать его от окружающей среды — значит уморить голодом.
Научный метод
Понятие эксперимента предполагает наличие теории. Без теории эксперимента нет, есть только наблюдение. С кибернетической (системной) точки зрения эксперимент — это управляемое наблюдение; управляющей системой является научный метод, который, опираясь на теорию, диктует постановку эксперимента. Таким образом, переход от простого наблюдения к эксперименту есть метасистемный переход в сфере опыта, и это первый аспект возникновения научного метода; второй его аспект — осознание научного метода как чего-то, стоящего над теорией, иначе говоря, овладение общим принципом описания действительности с помощью формализованного языка, о чем мы говорили в предыдущей главе. В целом возникновение научного метода — это единый метасистемный переход, который создает новый уровень управления, включающий управление наблюдением (постановка эксперимента) и управление языком (разработка теории). Новая метасистема — это и есть наука в современном смысле слова. В рамках этой метасистемы между экспериментом и теорией устанавливаются тесные связи — прямые и обратные. Бэкон описывает их так:
Наш путь и наш метод... состоят в следующем: мы извлекаем не практику из практики и опыт из опыта (как эмпирики), но причины и аксиомы из практики и опытов, а из причин и аксиом — снова практику и опыт, как истинные Истолкователи Природы2.
Теперь мы можем дать окончательный ответ на вопрос, что же произошло в Европе в начале XVII в.: произошел крупнейший метасистемный переход, захвативший как языковую, так и неязыковую деятельность. В сфере неязыковой деятельности он предстал в виде экспериментального метода. В сфере языковой деятельности он дал начало новой математике, которая развивается путем метасистемных переходов (эффект лестницы) по линии все углубляющегося самоосознания в качестве формализованного языка, служащего для создания моделей действительности. Этот процесс мы описали в предыдущей главе, не выходя за пределы математики. Теперь мы можем завершить его описание указанием на ту систему, в рамках которой этот процесс становится возможным.
Эта система — наука в целом с научным методом в качестве управляющего устройства, т. е. (расшифровывая эту краткую форму выражения) совокупность всех человеческих существ, занимающихся наукой и овладевших научным методом, вместе со всеми используемыми ими предметами. В главе 5, говоря об эффекте лестницы, мы обращали внимание, что он проявляется в том случае, когда существует метасистема Y, которая продолжает оставаться метасистемой по отношению к системам ряда X, X', X'', ..., где каждая следующая система образуется путем метасистемного перехода от предыдущей, и которая, оставаясь метасистемой, как раз и обеспечивает возможность метасистемных переходов меньшего масштаба от Х к X', от X' к X'' и т. д. Такая система Y обладает внутренним потенциалом развития; мы назвали ее ультраметасистемой. При развитии материального производства ультраметасистемой Y является совокупность человеческих существ, обладающих способностью превращать орудие труда в предмет труда. При развитии точных наук ультраметасистемой Y
является совокупность людей, овладевших научным методом, т. е. обладающих способностью создавать модели действительности с помощью формализованного языка.
Мы видели, что у Декарта научный метод, взятый в его языковом аспекте, послужил рычагом для реформы математики. Но Декарт не только реформировал математику; развивая тот же аспект того же научного метода, он создал множество теоретических моделей, или гипотез, для объяснения физических, космических и биологических явлений. Если Галилея можно назвать основоположником экспериментальной физики, а Бэкона — ее идеологом, то Декарт — и основоположник, и идеолог теоретической физики. Правда, модели Декарта были чисто механическими (других моделей тогда и не могло быть) и несовершенными, большая часть вскоре устарела. Однако это не так важно, как важно то, что Декарт утвердил принцип построения теоретических моделей. В XIX в., когда были накоплены первоначальные познания в физике и усовершенствован математический аппарат, этот принцип показал всю свою плодотворность.
Мы не сможем здесь даже в беглом обзоре коснуться эволюции идей физики и ее достижений, так же как идей и достижений других естественных наук. Мы остановимся на двух аспектах научного метода, имеющих универсальное значение, а именно на роли общих принципов в науке и на критериях выбора научных теорий, а затем рассмотрим некоторые следствия достижений новейшей физики ввиду их важного значения для всей системы науки и мировоззрения вообще. В заключение этой главы мы обсудим некоторые перспективы развития научного метода.
Наука и философия
Из формализованности языка науки вовсе не следует, что ученые могут ограничиться чисто формальным мышлением. Применение готовой теории требует действительно формальных операций, не выходящих за рамки определенного языка. Но создание новой теории — это всегда выход за рамки формальной системы, это всегда метасистемный переход большего или меньшего масштаба.
Конечно, никак нельзя сказать, что все те, кто не разрушает старых формализмов, занимаются вещами банальными и нетворческими. Это относится только к тем, кто действует в соответствии с уже имеющимися алгоритмами, выполняя по существу функции языковой машины. Однако достаточно сложные формальные системы не алгоритмизуемы и представляют широкое поле для творческой деятельности. Действие в рамках такой системы можно сравнить с игрой в шахматы. Чтобы хорошо играть в шахматы, надо долго учиться, запомнить много разных вариантов и комбинаций, приобрести специфическую шахматную интуицию. Так и ученый, имеющий дело со сложным формализованным языком (т. е. с математикой — чистой или прикладной), путем многолетнего обучения и тренировки развивает в себе интуицию своего языка, часто весьма узкого, и получает новые теоретические результаты. Это, конечно, деятельность и благородная, и творческая.
И все-таки выход за рамки старого формализма — это еще более серьезный творческий шаг. Если ученых, о которых мы говорили выше, можно назвать учеными-шахматистами, то ученых, создающих новые формализованные языки и теории, можно назвать учеными-философами. Пример сопоставления этих двух типов ученых мы видели в предыдущей главе — это пара Ферма-Декарт. Понятия новых теорий не возникают из пустоты в точном и формализованном виде. Они выкристаллизовываются постепенно в процессе абстрактного, но не формализованного, т. е. философского, мышления. Здесь также требуется интуиция, но интуиция другого рода — философская. «Наука, — писал Декарт в «Рассуждении о методе», — заимствует свои принципы из философии».
Создание фундаментальных научных теорий лежит в пограничной области между философией и наукой.
Пока ученый оперирует с привычными понятиями в рамках привычного формализованного языка, он не нуждается в философии. Он подобен шахматисту, переставляющему одни и те же фигуры на одной и той же доске, но решающему разные задачи. И он получает новые результаты, опираясь на свою шахматную, комбинаторную интуицию. Но при этом никогда не выйдет за пределы того, что заложено в его языке, в его шахматах. Улучшить сам язык, формализовать то, что еще не формализовано, — это, значит, прикоснуться к философии. Если новая теория не содержит этого элемента, то она является только следствием старых теорий. Можно сказать, что в каждой теории ровно столько нового, сколько в ней философии.
Из сказанного ясно, какое значение имеет философия для деятельности ученого. В «Диалектике природы» Ф.Энгельс писал:
Естествоиспытатели воображают, что они освобождаются от философии, когда игнорируют или бранят ее. Но так как они без мышления не могут двинуться ни на шаг, для мышления же необходимы логические категории, а эти категории они некритически заимствуют либо из обыденного общего сознания так называемых образованных людей, над которыми господствуют остатки давно умерших философских систем, либо из крох, прослушанных в обязательном порядке университетских курсов по философии (которые представляют собой не только отрывочные взгляды, но и мешанину из воззрений людей, принадлежащих к самым различным и по большей части к самым скверным школам), либо из некритического и бессистемного чтения всякого рода философских произведений — то в итоге они все-таки оказываются в подчинении у философии, но, к сожалению, по большей части самой скверной, и те, кто больше всех ругает философию, являются рабами как раз наихудших вульгаризованных остатков наихудших философских систем1.
Это звучит удивительно современно!
Наука и нравственность
Итак, наука претендует на роль верховного судьи и распорядителя всей жизни общества. Но справится ли она с этой ролью? Ведь людям нужны не только знание законов природы и умение ими пользоваться, им нужны еще определенные нравственные принципы — ответ на вопросы: что есть добро и что есть зло? К чему должен стремиться человек и чему противиться? Каковы смысл и цель существования каждого человека и всего человечества?
Может ли наука ответить на эти вопросы?
Строго говоря, нет. Без внесения дополнительных факторов наука на вопросы такого рода ответить не может. Идеи добра, цели, долга, входящие в нравственные принципы, лежат за ее пределами. Наука занимается построением моделей действительности, той действительности, которая есть на самом деле, а не той, которая должна быть. Она отвечает на вопросы: «Что есть на самом деле?», «Что будет, если сделать то-то и то-то?». Но просто на вопрос «что надо сделать?» без всяких «если» и «чтобы» она ответить принципиально не может. Как заметил один американский философ, сколько бы вы ни изучали расписание поездов, вы не сможете выбрать поезд, если не знаете, куда ехать. Все попытки построения нравственных принципов на научной основе неизбежно приводят, в конце концов, к вопросу «каково Высшее Благо?» или «какова Высшая Цель?», что в сущности одно и то же. Научные знания и логические умозаключения имеют отношение к нравственным проблемам лишь постольку, поскольку они помогают из ответа на этот общий, конечный вопрос вывести ответы на частные вопросы. Проблема Высшей Цели остается вне науки, и ее решение необходимо требует волевого акта, оно является, в конечном счете, результатом свободного выбора.
Значит ли это, что наука никак не влияет на решение этой проблемы? Отнюдь нет. Верная своему принципу исследовать все на свете, она может взглянуть со стороны на человека и на целые общества, решающие для себя проблему Высшей Цели, она может проанализировать различные аспекты этой ситуации и предсказать результаты, к которым приведет принятие того или иного решения. И этот анализ может существенно повлиять на решение проблемы, хотя и не изменит его природы как свободно производимого выбора.
Наука и производство
Подобно тому, как в эволюции животных был этап, когда формировалась центральная нервная система и, вследствие этого, происходили глубокие изменения в строении, поведении и внешнем облике организма, в развитии общества наступила сейчас эпоха бурных и глубоких перемен, происходящих под непосредственным воздействием науки. В начале первой промышленной революции роль науки была еще относительно небольшой, но затем последовали открытия в физике и химии, которые привели к революционным переменам в технике и условиях общественной жизни. В 50-х годах нашего столетия началась вторая промышленная революция, целиком обязанная достижениям науки. Сейчас она еще только набирает скорость, и даже ее ближайшие последствия трудно предвидеть заранее.
Наука стала непосредственной производительной силой — эта мысль, получившая теперь широкое признание, часто высказывается в печатных трудах и выступлениях. С другой стороны, она не может развиваться без развития промышленного производства и становится делом все более дорогостоящим. Современное производство требует не только использования голых рецептов науки, но и внедрения научного исследования и научного подхода во все свои звенья. Оно все более начинает походить на науку. В то же время наука, втягивая в себя значительную часть человеческих и материальных ресурсов общества, становясь массовой регулируемой деятельностью, приобретает черты производства. Наука и производство срастаются в единую иерархическую систему. Верхушечная почка испускает листья, которые сначала быстро растут, а затем застывают и превращаются в стандартные, устойчивые формы взаимодействия с материальной действительностью: электромоторы, самолеты, машины для производства синтетических тканей, генетические методы селекции. А почка поднимается все выше и плодит все новые и новые листья.
Нейрон
Внешний вид нервной клетки (нейрона) показан схематически на рис. 1.6. Нейрон состоит из довольно крупного (до 0,1 мм) тела, от которого отходят несколько отростков — дендритов, дающих начало все более и более тонким отросткам, подобно ветвям дерева. Кроме дендритов, от тела нервной клетки отходит еще один отросток — аксон, напоминающий длинный тонкий провод. Аксоны бывают очень длинны — до метра — и заканчиваются, подобно дендритам, древовидным разветвлением. На концах веточек, отходящих от аксона, можно видеть маленькие пластинки или луковички. Луковички одного нейрона близко подходят к различным участкам тела или дендритов другого нейрона, почти прикасаясь к ним. Эти контакты носят название синапсов; через них нейроны взаимодействуют друг с другом. Число луковичек, подходящих к дендритам одного нейрона, может исчисляться десятками и даже сотнями. Таким образом, нейроны очень тесно связаны друг с другом; они образуют нервную сеть.
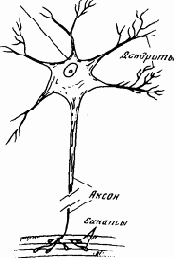
Рис. 1.6. Схема строения нейрона
С точки зрения физико-химических свойств, в первую очередь распределения электрического потенциала по поверхности клетки, нейрон может находиться в одном из двух состояний, которые называют состояниями покоя или возбуждения, и время от времени нейрон под воздействием других нейронов или каких-либо внешних факторов переходит из одного состояния в другое. Этот процесс, конечно, занимает некоторое время, так что исследователь, изучающий, например, динамику электрического состояния нейрона, рассматривает его как систему с непрерывными состояниями. Однако, сведения, которыми мы располагаем в настоящее время, указывают на то, что для работы нервной системы в целом существенным является не характер переходных процессов, а самый факт нахождения тех или иных нейронов в спокойном или возбужденном состоянии. Поэтому можно считать, что нервная сеть — это дискретная система, состоящая из элементарных подсистем — нейронов — с двумя состояниями.
Когда нейрон возбуждается, волна электрического потенциала бежит по аксону и доходит до луковичек на его разветвленных концах.
С луковичек через синапсы возбуждение передается на соответствующие участки клеточной поверхности других нейронов. Поведение нейрона зависит от состояния, в котором находятся его синапсы. Простейшая модель функционирования нервной сети исходит из предположения, что состояние нейрона в каждый момент времени есть однозначная функция состояния его синапсов. Экспериментально установлено, что возбуждение одних синапсов способствует возбуждению клетки, другие синапсы, напротив, будучи возбуждены, препятствуют возбуждению в клетке. Наконец, некоторые синапсы могут вовсе не проводить возбуждение от луковичек и, следовательно, не влиять на состояние нейрона. Установлено также, что проводимость синапса увеличивается после первого прохождения через него возбуждения и нескольких следующих прохождений. Происходит как бы замыкание контакта. Это объясняет, каким образом без изменения положения нейронов друг относительно друга может меняться система связей между нейронами и, следовательно, характер функционирования нервной сети.
Представление о нейроне как о мгновенном переработчике информации, поступающей от синапсов, является, конечно, сильно упрощенным. Нейрон, как и всякая клетка, — сложная машина, работа которой еще мало изучена. Эта машина обладает большой внутренней памятью, поэтому ее реакции на внешнее воздействие могут отличаться большим разнообразием. Однако, чтобы понять общие закономерности работы нервной системы, мы можем отвлечься от этих сложностей (у нас, собственно говоря, нет другого выхода!) и исходить из очерченной выше простой модели.
Неолитическая революция
В отличие от палеолитических культур неолитические культуры (известные как по археологическим, так и по этнографическим данным) отличаются большим разнообразием, специфичностью и локальностью. По технике производства орудий неолит представляет собой развитие качественного скачка (метасистемного перехода), сделанного в позднем палеолите: составные орудия, изготовляемые с помощью других орудий. На этом пути человечество совершает ряд выдающихся достижений, из которых самым замечательным является, по-видимому, изобретение лука. Большие перемены происходят также в одежде и устройстве жилищ.
Хотя в отношении изготовления орудий неолит не может похвастать крупномасштабным метасистемным переходом, в этот период все же происходит метасистемный переход огромной важности. Он затрагивает не орудия как таковые, а способ добывания пищи в целом (а, следовательно, опосредованно и орудия). Это переход от охоты и собирательства к скотоводству и земледелию. Его называют иногда неолитической революцией. Животные и растительный мир, которые до этого служили лишь сугубо внешним, не контролируемым источником пиши, становятся теперь (в определенной своей части, которая непрерывно увеличивается) объектом активного воздействия и управления со стороны человека. Мы имеем дело, таким образом, с типичным метасистемным переходом. Возникновение земледелия и скотоводства археологи относят ко времени около 7 тыс. лет назад (VI–V тысячелетие до н. э.), подчеркивая приблизительность этой даты. Из злаковых культур наиболее древними являются пшеница, просо, ячмень, рис. Позже появились рожь и овес. Первым домашним животным стала собака. Ее одомашнивание относится к раннему неолиту, еще до возникновения земледелия. С переходом к земледелию люди одомашнили свинью, овцу, козу, корову. Позже, уже в век металла, появились домашние лошадь и верблюд.
Нервная сеть
Общая схема нервной системы «кибернетического животного» в его взаимодействии с внешней средой представлена на рис. 1.7. Чувствительные нервные клетки, возбуждающиеся под действием внешних факторов, носят название рецепторов (т. е. получателей), ибо они служат первичным приемником информации о состоянии внешней среды. Эта информация поступает в нервную сеть и перерабатывается ею. В результате возбуждаются некоторые из нервных клеток, называемых эффекторами. Разветвления эффекторных клеток пронизывают те ткани организма, на которые нервная система оказывает непосредственное влияние. Возбуждение эффектора вызывает сокращение соответствующей мышцы или стимулирует деятельность соответствующей железы. Состояние всех рецепторов в некоторый момент времени назовем ситуацией в этот момент. (Точнее было бы говорить «результат воздействия ситуации на органы чувств», но это слишком длинно.) Состояние всех эффекторов назовем действием. Следовательно, роль нервной сети сводится к преобразованию ситуации в действие.
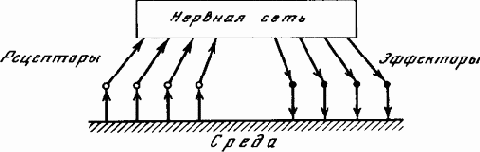
Рис. 1.7. Нервная система «кибернетического животного»
Под «средой» на рис. 1.7 удобно понимать не только предметы, окружающие животное, но также и его костно-мышечную систему и вообще все то, что не входит в состав нервной системы. Это снимает необходимость изображать на схеме отдельно тело животного и «не тело», тем более что никакого принципиального значения для деятельности нервной системы это разграничение не имеет. Важно лишь то, что возбуждение эффекторов приводит к определенным переменам в «среде». При том общем подходе к проблеме, который лежит в основе нашего рассмотрения, нам достаточно квалифицировать эти изменения как «полезные» или «вредные» для животного, не вдаваясь в дальнейшие подробности.
Какова задача нервной системы? Способствовать выживанию и размножению животного. Нервная система работает хорошо, когда возбуждение эффекторов приводит к полезным с этой точки зрения изменениям состояния среды, и плохо — в противном случае. Совершенствуясь в процессе эволюции, нервная система выполняет эту задачу все лучше и лучше. Каким образом это удается? Каким законам подчиняется процесс ее совершенствования?
Мы попытаемся ответить на эти вопросы, выделив в эволюции нервной системы животных несколько этапов, четко отличающихся между собой с кибернетической точки зрения, и показав, что из основного закона эволюции следует неизбежность перехода от каждого предыдущего этапа к каждому последующему. Так как в кибернетическую эру эволюция живых существ — это прежде всего эволюция их нервной системы, периодизация развития нервной системы дает периодизацию развития жизни в целом.
«Несуществующие» объекты
Мы уже говорили о «невозможных» числах: иррациональных, отрицательных, мнимых. С точки зрения платонизма использование таких чисел совершенно недопустимо, а соответствующие знаки бессмысленны. Однако индийские и арабские математики стали их понемногу использовать, а в современной математике они укоренились окончательно и бесповоротно и получили подкрепление в виде новых «несуществующих» объектов таких, как бесконечно удаленная точка плоскости. Но это произошло не сразу и возможность получать правильные результаты, оперируя с «несуществующими» объектами, долгое время представлялась удивительной и таинственной. В 1612 г. математик Клавий по поводу правила «минус на минус дает плюс» писал: «Здесь проявляется слабость человеческого разума, который не в состоянии постигнуть, почему оно может быть верным».
В 1674 г. Гюйгенс по поводу одного соотношения между комплексными числами замечает: «Здесь таится что-то для нас непонятное». «Непостижимые загадки математики» — любимое выражение начала XVIII столетия. Даже Коши в 1821 г. обладал еще весьма неясными представлениями о действиях над комплексными величинами3.
Последние сомнения и неясности, связанные с не интерпретируемыми объектами, исчезли только с введением аксиоматического подхода к математическим теориям и окончательным осознанием «языковости» математики. Сейчас мы считаем, что удивляться или противиться наличию в математике таких объектов не больше оснований, чем оснований удивляться или противиться наличию у автомобиля других деталей, кроме четырех колес, которые непосредственно соприкасаются с землей и приводят автомобиль в движение. Комплексные числа и тому подобные объекты — это внутренние «колесики» математических моделей, которые связаны с другими «колесиками», но не связаны непосредственно с «землей», т. е. элементами неязыковой действительности. Поэтому можно действовать с ними, как с формальными объектами (т. е. со знаками, нарисованными на бумаге), в соответствии с их свойствами, определяемыми' аксиомами. И не следует огорчаться из-за того, что вы не можете пойти в булочную и купить v-15 бубликов.
Нижний палеолит
Сделаем общий рисунок развития материальной культуры. Историю культуры до появления выплавки металлов делят на две эпохи: палеолит (древний каменный век) и неолит (новый каменный век). В каждой эпохе выделяют отдельные культуры, различающиеся географическим районом и временем, когда они существовали. Культурам, обнаруженным благодаря археологическим раскопкам, были присвоены названия, производные от названий тех мест, где они были обнаружены впервые.
Следы палеолитических культур найдены во многих районах Европы, Азии и Африки. Они позволяют уверенно произвести периодизацию развития культуры в палеолите, разбить палеолит на ряд стадий (эпох), имеющих универсальное значение для всех географических районов.
Древнейшая стадия — это так называемая шелльская культура, за ней следует ашельская, а за ней — мустьерская культура. Эти три стадии объединяются под общим названием нижнего (или раннего) палеолита. Начало нижнего палеолита относят ко времени порядка 700 тысяч лет тому назад, конец (поздняя мустьерская культура) — около 40 тысяч лет назад.
Шелльская и ашельская культуры знают лишь один вид каменного орудия — рубило. Шелльское рубило весьма примитивно — это грубо обитый с двух сторон камень, напоминающий по форме современный колун и примерно такого же размера. Типичное ашельское рубило меньше по размерам и гораздо лучше отделано, оно имеет тщательно заостренные края. Кроме того, на ашельских стоянках уже находят следы использования огня.
Орудия мустьерской культуры обнаруживают явную дифференциацию, здесь мы различаем по крайней мере два несомненно отличных типа каменных орудий: остроконечники и скребла. Техника обработки камня в мустьерский период существенно выше, чем в ашельский. Появляются предметы из кости и рога. Огонь употребляется повсеместно. Умели ли мустьерцы добывать огонь, в точности неизвестно, но очевидно, они умели его сохранять.
Человек нижнего палеолита — это еще в биологическом отношении не современный человек. Шелльская и ашельская культуры принадлежат людям (или полулюдям?) типа питекантропа и синантропа.
Мустье — культура неандертальцев. В нижнем палеолите развитие техники изготовления орудий (не только из камня, но также из дерева и других материалов, которые не сохранились до нашего времени) шло параллельно с развитием физических и умственных способностей человека, его эволюцией как вида. Увеличение объема мозга — самое убедительное свидетельство этой эволюции. Следующая табличка показывает вместимость черепной коробки у ископаемых людей, а также у современных человекообразных обезьян и человека (в см3):
|
Горилла |
600 – 685 |
|
Питекантроп |
800 – 900 |
|
Синантроп |
1000 – 1100 |
|
Неандерталец |
1100 – 1600 |
|
Современный человек |
1200 – 1700 |
Об аксиомах арифметики и логики
Первичные положения арифметики принципиально имеют ту же природу, что и первичные положения геометрии, но они, пожалуй, еще проще и очевидней, их отрицание еще более невообразимо, чем отрицание геометрических аксиом. Возьмем, например, аксиому, гласящую, что для любого числа a
a + 0 = a.
Число 0 изображает пустое множество. Можете ли вы представить себе, что от слияния некоторого множества с пустым множеством число элементов в нем изменится? Или вот еще одна арифметическая аксиома: для любых чисел a и b
a + (b + 1) = (a + b) + 1,
т. е. если единицу прибавить к числу b и результат сложить с а, то получим такое же число, как если бы мы сначала сложили a и b, а затем к результату прибавили единицу. Если проанализировать, почему мы не можем вообразить ситуацию, противоречащую этому утверждению, то мы увидим, что дело в тех же соображениях непрерывности, которые проявляются и в геометрических аксиомах. В процессе счета мы как бы проводим непрерывные линии, соединяющие считаемые предметы с элементами стандартного множества и, конечно, линии во времени (вспомним происхождение понятия «предмет»), непрерывность которых обеспечивает тождественность числа самому себе.
Естественный звуковой язык при перенесении его на бумагу порождает линейный язык, т. е. такую систему, все подсистемы которой суть линейные последовательности знаков. Знаки — это предметы, относительно которых предполагается только то, что мы умеем отличать одинаковые (тождественные) знаки от различных. Линейность естественных языков является результатом того, что звуковой язык развертывается во времени, а отношение следования во времени легко моделируется отношением порядка расположения на пространственной прямой. Специализация естественного языка привела к созданию математического линейного знакового языка, который в настоящее время образует основу математики.
Действуя в рамках линейных знаковых языков, мы постоянно пользуемся некоторыми их свойствами, которые представляются нам столь очевидными и само собой разумеющимися, что мы даже не даем себе труда сформулировать их в виде аксиом.
Возьмем для примера такое утверждение: если к символу (знаку) B
приписать слева символ A, а справа — символ C, то получится такое слово (последовательность знаков), как если к A приписать справа В, а затем C. Это и ему подобные утверждения обладают математической достоверностью, ибо мы не можем себе представить, чтобы было иначе. Один из разделов современной математики — теория полугрупп — изучает свойства линейных знаковых систем с аксиоматической точки зрения и простейшие из их свойств объявляет аксиомами.
И геометрические, и арифметические, и линейно-знаковые аксиомы имеют одну и ту же природу и опираются, в сущности, на одни и те же фундаментальные понятия, такие как тождество, движение, непрерывность, порядок. Никакой принципиальной разницы между этими группами аксиом нет. И если выбирать для них какой-то один термин, то их следовало бы назвать геометрическими или геометрически-кинематическими, так как все они отражают свойства нашего пространственно-временного опыта и пространственно-временного воображения. Более или менее значительное различие можно обнаружить лишь в группе «собственно геометрических» аксиом: некоторые аксиомы, касающиеся прямых и плоскостей, отражают более специфический опыт, связанный с существованием твердых тел. То же относится, по-видимому, и к метрическим понятиям. Впрочем, и это различие довольно условное. Можем ли мы говорить что-нибудь всерьез о тех понятиях, которые мы имели бы, если бы в мире не было твердых тел?
До сих пор речь шла лишь об абсолютной достоверности аксиом. А откуда у нас уверенность в достоверности утверждений, полученных из аксиом путем логического вывода?
Из того же источника: наше воображение отказывается допускать ситуацию, когда путем логического вывода мы из верных посылок получаем неверные результаты. Логический вывод состоит из последовательных шагов. На каждом шаге мы, опираясь на предшествующие утверждения, получаем новое утверждение. Из разбора формального логического вывода, который мы отложим до следующей главы, будет видно, что наша уверенность в том, что на каждом шаге мы из истинных утверждений можем получить только истинное утверждение, основывается на логических аксиомах2, которые представляются нам столь же достоверными, как и рассмотренные выше математические аксиомы, и по той же причине - абсолютной невообразимости противоположной ситуации.
Имея эту уверенность, мы приобретаем уверенность, что сколько бы шагов ни содержал бы логический вывод, он все равно будет обладать этим свойством. Здесь мы используем следующую важнейшую аксиому.
Аксиома индукции: Допустим, что функция f(x) оставляет неизменным свойство Р(х), т. е.
(?х){P(x)) ? P[f(x)]}.
Обозначим через fn(x) результат последовательного n-кратного применения функции f(x), т. е.
f1(x) = f(x), fn(x) = f[fn(x)].
Тогда при любом n функция fn(x) также оставляет неизменным свойство P(x), т. е.
(?n)(?х){P(x) ? P[fn(x)]}.
По своему происхождению и характеру логические аксиомы и аксиома индукции (которую относят к арифметике, так как она включает понятие числа) ничем не отличаются от остальных аксиом: все они суть математические аксиомы. Различие существует лишь в характере их использования. Когда математические аксиомы применяются к математическим утверждениям, они становятся элементами метасистемы. в рамках системы математически достоверных утверждений и мы называем их логическими аксиомами. Благодаря этому система математически достоверных утверждений становится способной к развитию. Великое открытие греков состояло в том, что можно прилагать достоверное к достоверному, и получать таким образом новое достоверное.
Объективизация времени
Теперь мы остановимся еще на одном интересном отличии языка хопи от среднеевропейского стандарта. В европейских языках множественное число и количественные числительные применяются в двух случаях: 1) когда они обозначают совокупность предметов, образующих реальную группу в пространстве, и 2) для классификации событий по времени, когда количественное числительное не соответствует никакой реальной совокупности. Мы говорим «ten men — десять человек» и «ten days — десять дней». Десять человек мы можем себе представить как реальную группу, например десять человек на углу улицы. Но десять дней мы не представляем в виде совокупности группы. Если это и группа, то воображаемая и состоящая не из «дней», ибо день не есть предмет, а из каких-либо предметов, которые связаны с днями лишь условно, например из листков календаря или отрезков на чертеже. Таким образом, временная последовательность и пространственная совокупность передаются у нас одним и тем же языковым аппаратом, и нам кажется, что это сходство лежит в самой природе вещей. В действительности же это совсем не так. Отношения «быть позже» и «быть расположенным вблизи» субъективно не имеют между собой ничего общего. Уподобление временной последовательности пространственной совокупности дано нам не в восприятии, а в языке. Это подтверждается существованием языков, в которых такое уподобление отсутствует.
В языке хопи множественное число и количественные числительные употребляются только для обозначения предметов, которые могут образовать реальную группу. Выражение «десять дней» не употребляется. Вместо «they stayed ten days — они пробыли десять дней» хопи скажет: «они уехали после десятого дня». Сказать «десять дней больше, чем девять дней» нельзя, надо сказать «десятый день позже девятого».
Европейское представление о времени Уорф называет объективизированным, ибо субъективное восприятие времени как чего-то «становящегося все более и более поздним» оно мысленно превращает в какие-то объективно (или, лучше сказать, объектно) данные, расположенные во внешнем пространстве предметы.
Это представление диктуется нашей языковой системой, которая для выражения отношения «позже-раньше» пользуется теми же самыми числами, которые измеряют пространственно данные количества, и теми же самыми словами, которые обозначают пространственные отношения. Это и есть объективизация. Такие термины, как «summer — лето», «September — сентябрь», «morning — утро», «sunset — заход солнца» являются у нас существительными, как и слова, обозначающие реальные предметы. Мы говорим «at sunset — на заходе солнца», так же как «at a corner — на углу», a «in September — в сентябре», как «in London — в Лондоне».
В языке хопи все временные термины — лето, утро и т. п. — представляют собой не существительные, а особые формы наречий, если употреблять терминологию среднеевропейского стандарта. Это — особая часть речи, отличающаяся от существительных, глаголов и даже от других наречий в хопи. Они не употребляются ни как подлежащие, ни как дополнения, ни в какой-либо другой функции существительного. Переводить их следует, конечно, как «летом», «утром» и т. д., но они не являются производными от каких-либо существительных. Объективизация времени полностью отсутствует.
Само понятие «время» в европейской культуре есть результат объективизации отношения раньше-позже в сочетании с представлением о веществе, субстанции. Мы создаем в своем воображении несуществующие предметы — год, день, секунда, а вещество, из которого они состоят, называем временем. Мы говорим «мало времени», «много времени» и просим дать час времени, как если бы мы просили литр молока. У хопи нет основы для термина с таким значением.
Трехвременная система глагола в среднеевропейском стандарте языка непосредственно отражает объективизацию времени. Время представляется бесконечной прямой, по которой передвигается (обычно слева направо) точка. Точка — это настоящее, левее ее — прошлое, правее — будущее. В языке хопи, как и можно было предполагать, все обстоит иначе. Глаголы здесь не имеют времен, подобных европейским. Глагольные формы отражают источник информации и ее характер.И это точнее соответствует действительности, чем трехвременная система. Ведь когда мы говорим «я завтра пойду в кино», это отражает не то, что на самом деле будет, а только наше намерение пойти в кино, намерение, которое существует сейчас и может перемениться в любую минуту. То же относится и к прошедшему времени.
Объекты и высказывания
Прежде чем продвигаться дальше в анализе языка и мышления, нам надо дать краткий набросок современной логики. Для наших целей достаточно рассмотреть только язык современной логики и те понятия, которые связаны с языком. Понятия, связанные с логическим выводом (доказательством), мы пока оставим в стороне.
Современная логика делит все сущее на объекты (или предметы) и высказывания (или утверждения). В естественном языке высказывания изображаются предложениями или наборами предложений, а объекты — словами и словосочетаниями, входящими в состав предложения. Примеры объектов: «цапля», «дядя Коля», «председатель колхоза». Примеры высказываний: «цапля сдохла», «дядю Колю выбрали председателем колхоза». Чаще всего объекты выражаются существительными, но это не обязательно. Например, «курить» — объект в высказывании «курить вредно». В приложении к математике объекты обычно называются термами, а высказывания соотношениями.
Примеры термов:
3.14. ax2 + bx + c. a?bf(z)dz.Примеры соотношений:
aх2 + bx + c = 0. 0 < z < 1. Каково бы ни было натуральное число n > 1, найдется простое число р, которое является делителем числа n. Сумма квадратов катетов равна квадрату гипотенузы.Понятия «объект» и «высказывание» считаются в логике первичными, интуитивно ясными и неопределяемыми. Формальное различие между ними состоит в том, что о высказывании имеет смысл говорить, что оно является истинным или ложным. Так, третий и четвертый примеры математических соотношений представляют собой истинные высказывания, а первое и второе соотношения могут быть истинными или ложными в зависимости от значения переменных х и z. К объектам понятия истинности и ложности неприменимы.
Объекты и высказывания, которые считаются элементарными, т. е. не расчлененными на отдельные составные части, обозначаются в логике буквами. Объекты обычно обозначаются малыми латинскими буквами, а высказывания — большими. Мы будем придерживаться этой символики, но дополнительно введем еще одно соглашение.
Для ясности записи и уменьшения словесных пояснений будем иногда обозначать элементарные объекты и высказывания словами и словосочетаниями, взятыми в кавычки. Следовательно, словосочетания в кавычках будут рассматриваться на равных правах с буквами.
Объекты и высказывания, которые не являются элементарными, конструируются, очевидно, из других объектов и высказываний. Мы должны указать теперь способ конструирования.
При наличии двух типов элементов (объекты и высказывания) и предполагая, что элементы, служащие строительным материалом, принадлежат все к одному типу, мы получаем четыре возможных типа конструкций, которые мы сведем в следующую таблицу.
|
Что конструируется |
Из чего конструируется |
Название конструкции |
|
Высказывание |
Высказывания |
Логическая связка |
|
Высказывание |
Объекты |
Предикат |
|
Объект |
Высказывания |
— |
|
Объект |
Объекты |
Функция |
Обломки системы понятий
У человека понятия нижайшего уровня, относящиеся к зрительному восприятию, вероятно, мало отличаются от понятий лягушки. Во всяком случае, структура сетчатки у млекопитающих и человека такая же, как и у земноводных.
Некоторое представление о понятиях следующих уровней иерархии дает явление нарушения восприятия стабилизированного на сетчатке изображения. Это очень интересное явление. Оно состоит в следующем.
Когда человек смотрит на неподвижный объект, «фиксирует» его глазами, глазные яблоки не остаются абсолютно неподвижными, а созерцают небольшие непроизвольные движения. В результате изображение объекта на сетчатке находится в постоянном движении, складывающемся из медленного дрейфа и скачкообразных смещений, возвращающих изображение к точке максимальной чувствительности. Оно «топчется на месте» в окрестности этой точки.
Можно создать на сетчатке стабилизированное, не топчущееся на месте изображение. Для этого надо, очевидно, чтобы объект был жестко связан с глазным яблоком и двигался вместе с ним. Достигается это так (рис. 2.4). На глаз надевают контактную линзу, к которой прикреплен маленький стерженек. Стерженек несет миниатюрный оптический проектор4, в который можно вставлять диапозитивы размером в несколько миллиметров. Испытуемый видит изображение как удаленное в бесконечность. Так как проектор поворачивается вместе с глазом, изображение на сетчатке неподвижно.
При предъявлении испытуемому стабилизированного изображения он в течение первых нескольких секунд воспринимает его как при нормальном зрении, но затем начинаются нарушения. Изображение то исчезает, заменяясь серым или черным фоном, то появляется частями или целиком.
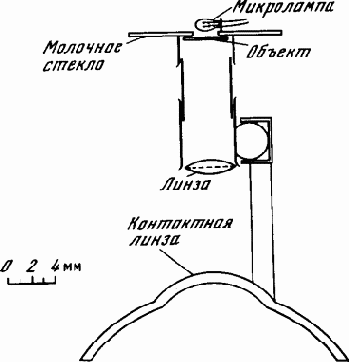
Рис. 2.4. Устройство для стабилизации изображения на сетчатке
Уже сам факт неправильного восприятия стабилизированного изображения весьма примечателен. С логической точки зрения нет никакой необходимости, чтобы изображение неподвижного объекта гуляло по сетчатке. Количество информации от этого не увеличивается, а обрабатывать ее становится труднее.
И действительно, когда аналогичные задачи встают в области техники, например, при передаче изображения по телевизору или при вводе информации с экрана в вычислительную машину, то предпринимаются специальные усилия, чтобы стабилизировать изображение. А человеческий глаз не только приспособлен к прыгающему изображению, но и решительно отказывается принимать изображение, если оно неподвижно. Это свидетельствует о том, что понятия, связанные с движением, подобные, вероятно, тем, которые мы наблюдали у лягушки, глубоко укоренились где-то в нижних этажах иерархии, и если соответствующие классификаторы вывести из игры, то правильная обработка информации нарушится. С точки зрения конструктора сложного аппарата, подобного глазу (плюс обработка информации), такое устройство является странным. Конструктор, наверное, все нижние этажи занял бы статическими понятиями, а описание движения объектов уже проводил бы в терминах более высокого уровня. Но иерархия зрительных понятий возникла в процессе эволюции. Для наших далеких лягушкоподобных предков были чрезвычайно важны понятия, связанные с движением, и им некогда было ждать, пока у них разовьются сложные статические понятия. Поэтому примитивные динамические понятия возникли на самых ранних этапах развития нервной системы, а так как природа использует найденные ею блоки на следующих этапах строительства, эти понятия прочно закрепились в самом низу иерархии понятий. Чтобы они могли работать, глазному яблоку приходится совершать «броуновские» движения.

Рис. 2.5. Фрагментация стабилизированного изображения
Еще интереснее характер распада изображения на части (фрагментация). Простые фигуры, например, одиночный отрезок, исчезают и восстанавливаются целиком. Более сложные фигуры иногда также исчезают целиком, а иногда распадаются на части, которые исчезают и появляются независимо друг от друга (рис. 2.5). Фрагментация происходит не хаотично и не независимо от вида изображения, как бывает, например, когда рисунок на доске стирают тряпкой, а в соответствии с «истинной» структурой изображения.
Слово «истинная» мы берем в кавычки потому, что на самом деле, конечно, фрагментация происходит в соответствии со структурой восприятия изображения системой глаз — мозг. Мы не знаем в точности, какова механика нарушения восприятия при стабилизации, мы знаем только сам факт, что стабилизация выводит из строя какой-то компонент системы восприятия. Но и отсюда можно сделать некоторые выводы. Представьте себе, что в архитектурном сооружении внезапно исчезли, растворившись в воздухе, несколько важных элементов конструкции. Здание развалится, но, вероятно, на части очень различных размеров. Здесь вы видите отдельные кирпичи и куски стекла, там — часть стены и крыши, а там сохранился целый угол дома. Примерно такое зрелище и являет собой восприятие стабилизированного изображения. Оно дает возможность представить характер понятий высшего уровня (или высших уровней), но не оценить их взаимные связи и зависимости. Надо отметить, что в формировании понятий высшего уровня у человека большую роль играет его личный жизненный опыт — обучение, если говорить языком кибернетики. (Это будет следующим этапом эволюции нервной системы, так что здесь мы несколько забегаем вперед. Но для исследования иерархии понятий не имеет большого значения, получена она по наследству или благоприобретена своим трудом.)
Приведем несколько выдержек из упомянутой выше работы.
Контурный человеческий профиль всегда исчезает и восстанавливается отдельными дискретно организованными элементами. Передняя часть лица, задняя сторона головы, комплекс линий вокруг глаз или вокруг уха исчезают и появляются вновь как целые элементы, в отдельности друг от друга или в различных комбинациях. В противоположность этому рисунок, состоящий из многих волнистых линий, расположенных неупорядоченно, при первом же предъявлении воспринимается как чрезвычайно активный объект. Отдельные завитки быстро исчезают и восстанавливаются... Эти изменения происходят так быстро, что испытуемые не могут дать точного отчета о них. После длительного рассматривания небольшие группы завитков начинают исчезать и восстанавливаться как единые элементы.
Эти заново оформленные комбинации сохраняются в течение более долгих промежутков времени...
Важность линейной организации как фактора группировки подчеркивается фрагментацией стабилизированного изображения, состоящего из ряда квадратиков. Видимыми обычно остаются полный горизонтальный, вертикальный или диагональный ряды, которые затем также исчезают, и остается лишь отдельный квадратик во всем поле зрения. Иногда исчезают все одноименные стороны квадратиков... Если предъявляются беспорядочно разбросанные точки, то могут исчезнуть отдельные группы точек, а оставшиеся располагаются приблизительно вдоль одной линии... При рассматривании рисунка, состоящего из прямых линий, эти последние воспринимаются как независимые друг от друга, причем рисунок разбивается на части в местах пересечения. Линии исчезают и появляются вновь как единое целое либо поодиночке, либо вместе с другими; вместе часто появляются параллельные линии. При замене рисунка, состоящего из линий, затушеванной фигурой вместо линий независимыми элементами становятся углы. Исчезновение стабилизированного изображения начинается с центра, а резко очерченные углы исчезают по очереди. При восстановлении изображения оно появляется полностью или частично с резко очерченными углами.
Обратный ход модели
Фаза исследования только что созданной теории включает деятельность по двум направлениям. Первое — это всесторонняя проверка теории, сравнение ее с опытом, поиск изъянов. Но допустим, теория хороша. Тогда на первый план выступает второе направление — попытка дать модели «обратный ход», т. е. по заданному L2 определить те или иные особенности L1. Эта процедура отнюдь не лишена практического смысла. Человек использует модель для планирования целенаправленной деятельности, он хочет знать, что ему надо делать, чтобы получить требуемый результат, какое должно быть L1, чтобы получить данное L2. В нашем примере с земледельцем вопрос может быть поставлен, например, так: при известной ширине поля какова должна быть его длина, чтобы получить заданное количество пшеницы?
Однако не всегда исследование обратного хода модели диктуется сиюминутными потребностями практики. Часто это делается из чистого любопытства, по принципу «интересно, что получится?» Тем не менее, результатом такой деятельности будет лучшее понимание устройства и свойства модели и создание новых конструкций и моделей, т. е., в конечном счете, многократно увеличенная польза для практики. В этом состоит высшая мудрость природы, наделившей человека «чистым» любопытством.
В арифметике обратный ход модели приводит к понятию уравнения. Простейшие уравнения порождают операции вычитания и деления. Пользуясь современным алгебраическим языком, мы определяем разность b - a как решение уравнения a + x = b, т. е. такое число x, что это равенство становится верным. Аналогично определяется частное от деления b на a. Операция деления порождает новую конструкцию — дробь. Повторное умножение числа на самое себя порождает конструкцию степени, а обратный ход при наличии этой конструкции — операцию извлечения корня. Это завершает перечень арифметических конструкций, которые были в употреблении у древних египтян и вавилонян.
Определение сложного рефлекса
Подводя итог описанию четвертого этапа развития, мы можем определить сложный рефлекс как такой процесс, когда возбуждение рецепторов, вызванное взаимодействием с внешней средой, передается по нервной сети, преобразуясь ею, и активизирует определенный план действий, который тут же начинает выполняться. В этой схеме поведения все обратные связи между организмом и средой осуществляются в процессе регулирования действий планом, а в целом взаимодействие между средой и организмом описывается классической формулой стимул — реакция. Только теперь реакция — это активизация того или иного плана.
1 Позже мы дадим несколько более общее определение понятия, а множество ситуаций назовем аристотелевским понятием. Сейчас мы опускаем прилагательное «аристотелевский» для краткости.
2
Согласно терминологии, принятой многими логиками, противопоставление абстрактных понятий конкретным — это совсем не то же самое, что противопоставление общих понятий единичным. В учебнике логики (Логика. М.: Госполитиздат, 1956) читаем: «Понятие, посредством признаков которого предмет мыслится как таковой и как данный предмет, называется конкретным. Понятие, посредством признаков которого мыслится не данный предмет как таковой, а некоторое свойство предмета или отношение предметов, называется абстрактным».
Из этого определения, которое трудно назвать шедевром ясности мысли, можно все-таки заключить, что общие понятия, которые образуются не путем перечисления единичных объектов, входящих в него, а путем указания ряда признаков, объявляемых существенными, и отвлечения от остальных (несущественных) признаков, можно также считать абстрактными. Мы будем рассматривать только такие общие понятия и будем называть их также абстрактными. Например, абстрактный треугольник — это любой треугольник, независимо от величины его сторон и углов и его положения на экране, следовательно, это абстрактное понятие. Такое употребление термина «абстрактный» имеет место в обиходе, а также в математике. В то же время, согласно учебнику логики, «треугольник», «квадрат» и т. п. суть конкретные общие понятия, а вот «треугольность» и «квадратность», которые им свойственны, это понятия абстрактные. По существу, здесь в ранг логического возводится чисто грамматическое различие, ибо даже с точки зрения сторонника последнего варианта терминологии обладание абстрактным понятием равнозначно обладанию соответствующим общим понятием.
3 Pyc. пер. см. в сб.: Электроника и кибернетика в биологии и медицине. М.: Изд-во Иностр. Лит., 1963.
4 См.:Причард Р. Изображение на сетчатке и зрительное восприятие // Проблемы бионики. М.: Мир, 1965. Пер. с англ.: Pritchard R. Stabilized image on the retine // Sci. Amer. 1961. Vol. 204, N 6. P. 72-78.
Орудия для производства орудий
Вернемся к материальной культуре и эффекту лестницы. Предметы и орудия труда являются частями, подсистемами той системы, которую мы назвали выше «сверхсуществом», возникающим благодаря развитию человеческого общества. Теперь мы будем называть это сверхсущество просто культурой, понимая под этим как ее физическое «тело», так и способ функционирования («физиологию») в зависимости от контекста. Итак, предметы и орудия труда > подсистемы культуры. Они могут обладать своей собственной сложной структурой и входить в соответствии со способом их использования в состав наиболее крупных подсистем культуры, также обладающих внутренней структурой.
В частности, само членение материальных подсистем на предметы труда и орудия труда имеет глубокий смысл и отражает структуру производства. Когда к предметам определенного класса A человек применяет орудие B, то это орудие вместе с предметами A образует уже метасистему по отношению к подсистемам A. Действительно, подсистема B непосредственно действует на подсистемы A и для этой цели специально и создается. (Конечно, это воздействие происходит не без участия человеческой руки и мозга, которые входят в состав всякой производственной системы.) Итак, появление орудия для обработки каких-то предметов, которые ранее не обрабатывались, есть метасистемный переход в рамках системы производства. Как мы видели, умение создавать орудия — одно из первых следствий очеловечивания. И, поскольку человек остается постоянной движущей силой производственной системы, метасистемный переход от предмета труда к орудию труда может повторяться сколько угодно раз. Создав орудие B для обработки предметов класса A, человек начинает думать, как бы его усовершенствовать, и изготовляет орудие C для изготовления орудий класса B. На этом он, конечно, не останавливается и изобретает орудие D для улучшения орудий класса C. И так далее. Орудие труда неизменно превращается в предмет труда. Это — эффект лестницы. Важно освоить сам принцип изготовления орудий — научиться залезать на ступеньку. Дальше все пойдет само собой: система производства становится ультраметасистемой, способной к развитию. Плод этого процесса — современная промышленность, сложившаяся многоуровневая система, которая использует природные материалы, и шаг за шагом превращает их в свое «тело» — сооружения, машины, приборы подобно тому, как живой организм усваивает съеденную пищу.
Ошибка природы
Мы уже приводили процесс счета в качестве примера использования модели действительности, которая не содержится в мозгу, а создается на уровне языка. И это очень яркий пример. Счет основан на способности расчленять окружающий мир на отдельные предметы. Эта способность возникла довольно давно в ходе эволюции; высшие позвоночные обладают ею, по-видимому, в такой же мере, как и человек. Ясно, что для успешной борьбы за существование живому существу, умеющему различать отдельные предметы, было бы небесполезно также уметь их считать (это помогло бы, например, ориентации в незнакомой местности). Описание с помощью чисел является естественным интегральным дополнением к дифференциальному описанию с помощью распознавания отдельных предметов. С другой стороны, кибернетический аппарат для распознавания чисел, т. е. для счета, может быть чрезвычайно простым. Эта задача гораздо более легкая, чем различение отдельных предметов. Поэтому можно было бы ожидать, что распознавание чисел в пределах, обусловленных устройством органов зрения, появится в ходе эволюции. Человеческий глаз может различать одновременно десятки и сотни отдельных предметов. Мы могли бы ожидать, что с одного взгляда будем также легко отличать совокупность из двухсот предметов от совокупности из двухсот одного, как два предмета отличаем от трех.
Однако природа не пожелала или не сумела дать нам этой способности. Непосредственно распознаваемые числа смехотворно малы — обычно до четырех — пяти. С помощью тренировки можно немного продвинуться вперед, но делается это путем мысленного разбиения на группы или запоминания картины в целом с последующим счетом в уме. Ограничение на непосредственное распознавание остается. Оно никак не связано с устройством органов зрения и обусловлено, очевидно, какими-то более глубинными особенностями строения мозга. Какими же? Пока не знаем. Одно обстоятельство заставляет задуматься и подсказывает некоторые предположения. Вот оно.
Кроме пространственного распознавания чисел, есть еще временное распознавание.
Двойной стук в дверь мы никогда не спутаем с тройным или одинарным. Но восемь или десять ударов это уже заведомо «много», и различать такие звуки мы можем только по их суммарной продолжительности (это соответствует суммарной площади, занятой однородными предметами при пространственном распознавании). Предел, ограничивающий оба вида распознавания чисел, одинаков. Случайно ли это совпадение? Быть может, непосредственное распознавание чисел всегда имеет временную природу и ограничено емкостью мгновенной (оперативной) памяти — числом ситуаций, которые она вмещает. Ограничение на пространственное распознавание объясняется при этом предположении тем, что зрительное изображение развертывается во времени (при этом происходит быстрое переключение внимания с предмета на предмет, о чем говорилось выше) и подается для анализа на тот же самый аппарат.
Так или иначе, но в нашем мозговом устройстве природа оставила досадную недоделку и свою работу по созданию «продолжения мозга» человек начинает с исправления ее ошибки: он учится считать. Так начинается математика.
Основной закон эволюции
В процессе эволюции жизни, насколько нам известно, всегда происходило и происходит сейчас увеличение общей массы живого вещества и усложнение его организации. Усложняя организацию биологических образований, природа действует по методу проб и ошибок. Существующие образования воспроизводятся во многих экземплярах, которые, однако, не вполне тождественны оригиналу, а отличаются от него наличием небольших случайных вариаций. Эти экземпляры служат затем материалом для естественного отбора. Они могут выступать и как отдельные живые существа — тогда отбор приводит к закреплению полезных вариаций, и как элементы более сложного образования — тогда отбор направлен также и на структуру нового образования (например, при возникновении многоклеточных организмов). И в том и в другом случае отбор является результатом борьбы за существование, в которой более жизнеспособные образования вытесняют менее жизнеспособные.
Этот механизм развития жизни, открытый Чарльзом Дарвином, можно назвать основным законом эволюции. В наши цели не входит обоснование или обсуждение этого закона с точки зрения тех законов природы, которые можно было бы провозгласить более фундаментальными. Будем принимать основной закон эволюции как нечто данное.
Отношение как объект
Тот факт, что греки не создали алгебры, имеет глубокие корни и в философии. У них не было даже арифметической алгебры — это первое и наиболее внешнее, можно даже сказать побочное, следствие их философии. Их мало интересовали арифметические уравнения, ведь уже уравнения второй степени не имеют, вообще говоря, точных числовых решений. А приближенные вычисления и все, что было связано с практическими задачами, их не интересовало. Зато решение могло быть найдено путем геометрического построения! Но, если даже предположить, что греческие математики школы Платона познакомились бы с арифметической буквенной символикой, трудно представить, чтобы они воспроизвели научный подвиг Декарта. Ведь отношение не было для них идеей и не имело, следовательно, реального существования. Кому же придет в голову обозначать буквой то, чего нет? Платоновская идея — это обобщенный образ, форма, свойство: то, что можно представить в воображении как более или менее обобщенный предмет. Все это является первичным и имеет независимое существование, причем существование даже более реальное, чем чувственно воспринимаемые вещи. А что такое отношение отрезков? Попробуйте его представить, и вы сразу увидите, что представляете себе никакое не отношение, а просто два отрезка. Понятие отношения величин отражает процесс измерения одной из них с помощью другой. Но процесс — это не идея в платоновском понимании, это нечто вторичное и не существующее реально: идеи вечны и неизменны и хотя бы уже поэтому не имеют ничего общего с процессами.
Интересно, что понятие отношения величин, отражающее свойства процесса измерения, было в строгой математической форме введено еще Евдоксом и вошло в пятую книгу «Начал» Евклида. Именно это понятие и было использовано Декартом. Однако объектом отношение не было ни у Евдокса, ни у последующих греческих математиков; будучи едва введено, оно немедленно уступило место пропорции, которую легко представить как свойство четырех отрезков, образуемых при пересечении сторон угла двумя параллельными линиями.
Понятие отношения величин — это языковый конструкт, и довольно сложный, а платонизм мешал вводить а математику конструкты, ограничивал ее базисные понятия четко представимыми статическими пространственными образами. В школе Платона даже дроби считались чем-то незаконным с точки зрения настоящей математики. В «Государстве» мы читаем: «Если ты захочешь делить единицу, то ученые математики высмеют тебя и не позволят это сделать; если же ты размениваешь единицу на мелкие деньги, они полагают её обращенной во множество и остерегаются рассматривать единицу не как единое, но состоящее из многих частей». При таком отношении к рациональному числу, что уж говорить об иррациональном!
Кратко подвести итог влиянию платоновского идеализма на греческую математику можно следующим образом. Осознав математические утверждения как объект работы, греки совершили метасистемный переход огромной важности, но они тут же объективизировали базисные элементы математических утверждений, стали рассматривать их как часть неязыковой действительности — «мира идей». Тем самым они закрыли себе путь к дальнейшей эскалации критического мышления — осознанию базисных элементов (понятий) математики как явлений языка и созданию все более и более сложных математических конструктов. Развитие математики в Европе было непрерывным освобождением от оков платонизма.
Память
Путем редупликации может быть получено, в принципе, сколько угодно фиксаторов представлений. Но тут возникает вопрос: а сколько их нужно животному? Сколько нужно дубликатов «осведомленных» классификаторов? Один? Два? Десять?
Из общих соображений следует, что дубликатов нужно много. Ведь фиксаторы представления служат для организации опыта и поведения во времени. Фиксатор цели хранит ситуацию, которая должна, по идее, осуществиться в будущем. Другие фиксаторы могут хранить ситуации, которые реально были в прошлом. Временная организация опыта необходима животному, стремящемуся приспособиться к среде, в которой оно живет, ибо эта среда обнаруживает некоторые закономерности, т. е. корреляции между прошлыми и будущими ситуациями. Можно предсказать, что после какого-то начального увеличения числа рецепторов дальнейшее совершенствование нервной системы потребует создания фиксаторов представлений, причем создания их в большом числе. Ибо нет смысла продолжать наращивать число рецепторов и классификаторов и улучшать тем самым «мгновенные снимки» окружающей среды, если система не умеет обнаруживать корреляции между ними. Но чтобы обнаружить корреляции между «мгновенными снимками», надо их где-то хранить. Так и возникают фиксаторы представлений, иначе говоря память. Хранение цели в процессе регулирования — это простейший случай использования памяти.
Переход к феноменологическому описанию
Итак, формально, действие на функциональной схеме — это множество состояний. Но сказать, что данное действие есть какое-то множество, — это почти ничего не сказать. Надо уметь определить это множество. И если мы не знаем структуры системы и способа ее функционирования, то сделать это строго практически невозможно. Остается довольствоваться неполным, феноменологическим определением, основанным на внешне проявляемых следствиях внутренних состояний. Вот такими-то функциональными схемами с более или менее точно определенными действиями в вершинах графа и описывается поведение сложных, неизвестно как устроенных систем, подобных животным или человеку. Схемы на рис. 2.10 и 2.11 являются, конечно, именно такими схемами. Феноменологический подход к деятельности мозга осуществляется двумя науками: психологией и бихевиористикой (изучение поведения). Первая основана на наблюдениях субъективных (изнутри), вторая — объективных (извне). Они тесно связаны между собой, и часто их объединяют под общим названием психологии.
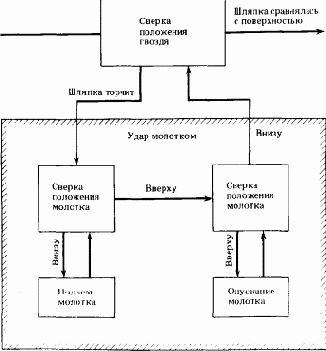
Рис. 2.14. Иерархический план забивания гвоздя
Так как операционный компонент единицы T-O-T-E может быть составным и требовать выполнения нескольких подчиненных планов, единицы T-O-T-E могут иметь иерархическую структуру. Миллер, Галантер и Прибрам приводят следующий пример. Если удар молотком по гвоздю представить как двухфазное действие, слагающееся из подъема и опускания молотка, то функциональная схема на рис. 2.11, изображающая план забивания гвоздя, перейдет в схему на рис. 2.14. Эта схема в свою очередь может входить в качестве элемента в операционный компонент схемы T-O-T-E более высокого уровня.
Мы видели, что элементарной функциональной схеме на рис. 2.10 соответствует элементарная структурная схема на рис. 2.6. Что происходит со структурной схемой, когда планы образуют иерархию? Точнее, наоборот: какие структурные схемы могут обеспечить выполнение иерархически построенного плана?
Можно предположить различные варианты таких схем. Например, можно представить, что блок сравнения всегда один и всегда пользуется одной и той же подсистемой, хранящей цель, но состояние этой последней (т.
е. цели) меняется под действием других частей системы, обеспечивая вытекающую из плана смену целей. Напротив, можно представить, что пара — блок сравнения и цель — размножается многократно, и при выполнении иерархического плана управление переходит от одной пары к другой. Можно предположить комбинацию этих двух способов. И вообще можно придумать множество различно устроенных кибернетических устройств, осуществляющих одну и ту же иерархическую функциональную схему. Ясно только, что они будут иметь иерархическую структуру и что устройства такого типа могли возникнуть эволюционно путем редупликации подсистем и отбора полезных вариантов.
Каковы же структурные схемы, реально возникшие в процессе эволюции? Увы, пока мы этого достоверно не знаем. Поэтому-то нам и пришлось перейти к функциональным схемам. И это только первое из ограничений, которые мы будем вынуждены накладывать на стремление к точному кибернетическому описанию высшей нервной деятельности. Мы очень мало знаем сейчас о кибернетической структуре и работе мозга высших животных и, тем более, человека. Собственно говоря, мы почти ничего не знаем. Есть только отдельные факты и предположения. Поэтому в дальнейшем анализе нам придется опираться главным образом на феноменологию — данные бихевиористики и психологии, где дело обстоит несколько лучше. Что касается кибернетического аспекта, то мы перейдем на уровень чрезвычайно общих понятий. На этом уровне мы обнаружим определенные закономерности, столь общие, что они объясняют этапы развития как нервной системы, так и человеческой культуры и, в частности, науки. Тот относительно конкретный анализ первых этапов эволюции нервной системы, который позволило нам сделать нынешнее состояние знаний, послужит нам разбегом для последующего более абстрактного анализа. Конечно, нашей истинной целью является именно этот абстрактный анализ, но было бы приятнее, если бы, зная кибернетику мозга, мы могли совершить переход от конкретного к абстрактному более плавно и обоснованно.
Пятна и линии
Обратите внимание: мы свели понятие линии к понятию пятна. Мы должны были это сделать потому, что подводили теоретическую базу под существование соответствующих классификаторов. Действительно, из двумерной непрерывности изображения на сетчатке можно сделать вывод, что основным понятием для мозга должно быть понятие пятна, а не линии. Линия может входить либо как пятно экзотической формы, либо как граница между пятнами. Это теоретическое соображение подтверждается многими наблюдениями.
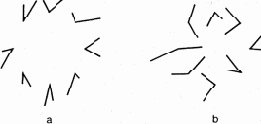
Рис. 3.5. Маскировка круга, образуемого вершинами углов
На рис. 3.5,а отчетливо виден круг, образованный вершинами углов. На соседнем рисунке вершины углов расположены в точности так же, но стороны их направлены хаотически как наружу, так и внутрь круга. В результате круг исчезает. Можно проследить за вершинами, перенося внимание с одной на другую, и убедиться, что они расположены на окружности, но увидеть это подобно тому, как это видно на первом рисунке, не удается. И это несмотря на то, что точки, образующие окружность, все являются вершинами углов и нет ни одной вершины, не лежащей на окружности. Даже самая простая программа машинного распознавания окружностей «увидела» бы на рис. 3.5,б (как и на рис. 3.5,а) окружность. Между тем наш глаз ее не видит. А на рис. 3.5,а, где все лучи направлены наружу, наш глаз размазывает их в некое подобие обода и ясно видит внутренний круг — двумерное образование, пятно. Становится видна и окружность — граница этого пятна.

Рис. 3.6. Иллюзия сближения диагоналей
Есть много зрительных иллюзий, являющихся следствием того, что мы «видим пятна», и дающих поучительные примеры врожденных ассоциаций. Одна из лучших представлена на рис. 3.6. Фигура а — квадрат и его диагонали пересекаются под прямым углом. Фигура б построена из дуг окружностей, но вершины ее образуют в точности такой же квадрат, как и на фигуре а, и, следовательно, диагонали также пересекаются под прямым углом. В это почти невозможно поверить — так велика иллюзия, что диагонали фигуры б приближены к вертикали.
Эту иллюзию можно объяснить тем, что вместе с микрохарактеристиками фигуры, т. е. с деталями ее формы, мы всегда воспринимаем и ее макрохарактеристику — общий облик. Общий облик фигуры б - пятно, вытянутое по вертикали. О степени вытянутости можно судить по фигуре в. Это прямоугольник, площадь которого равна площади фигур а и б, а отношение ширины к высоте равно отношению средней ширины фигуры б к ее средней высоте. Гипотетический классификатор, регистрирующий общую вытянутость фигуры, придет при созерцании фигуры б в такое же состояние, как при созерцании прямоугольника в. Иначе говоря, хотим мы того или нет, но фигура б у нас ассоциируется с прямоугольником в. Проводя мысленно диагонали в фигуре б, мы отождествляем их с диагоналями прямоугольника в, которые образуют острые вертикальные углы. Классификатор, регистрирующий вытянутость пятна — вещь, несомненно полезная, особенно полезен был он для наших далеких предков, которые и не воспринимали мир в более тонких понятиях. Но из-за того, что мы не можем включать и выключать его по желанию, он оказывает нам иногда дурную услугу, вызывая обман зрения.
Платонизм в ретроспективе
Идеализм Платона — результат своеобразной проекции элементов языка в действительность. «Идеи» Платона имеют то же происхождение, что и духи первобытного мышления, — это воображаемые значения реально существующих имен. На первых этапах развития критического мышления еще не существует правильного понимания природы абстрагирования и взаимоотношения между языковыми объектами и неязыковой деятельностью. Первобытный комплекс имя-значение еще навязывает представление о взаимно однозначной связи между именем и значением. Для слов, обозначающих определенный, единственный предмет, взаимная однозначность как будто имеет место, ибо предмет мы представляем себе как что-то одно. А как быть с общими понятиями (универсальными)? В сфере реально существующего для значений вообще не остается места, все расхватано «единичными» понятиями — ведь к каждому предмету можно подкрепить бирку с именем. Образующуюся пустоту и заполняет «идея». Подчеркнем, что идеализм Платона отнюдь не включает утверждения о примате духовного над материальным, т. е. не является спиритуализмом (этот термин, широко используемый в западно-европейской литературе, у нас мало употребителен и часто заменяется термином «идеализм», что приводит к неточностям). Духовный опыт, по Платону, это такая же эмпирия, как чувственный опыт, и никакого отношения к миру идей не имеет. «Идеи» Платона — чистые призраки, причем призраки, порожденные не духовным, а чувственным опытом.
С современной кибернетической точки зрения единичным понятием можно считать только строго определенную, единичную ситуацию, т. е. указание всех рецепторов, образующих вход нервной системы. Нечего и говорить, что субъективно мы совершенно не осознаем единичных, в этом смысле, понятий. Близкие ситуации становятся неразличимыми где-то на самых ранних стадиях обработки информации, и представления, с которыми имеет дело наше сознание, это обобщенные состояния, т. е. общие, или абстрактные понятия (множество ситуаций). Понятия об определенных предметах, которые традиционная логика наивно принимает за первичные элементы чувственного опыта и называет «единичными» понятиями, в действительности, как показано выше, являются весьма сложными конструкциями, требующими анализа киноленты ситуаций и опирающимися на более элементарные абстрактные понятия, такие, как непрерывность, форма, цвет, пространственные отношения и т.
п. Причем чем «конкретнее» понятие с точки зрения логики, тем сложнее оно с точки зрения кибернетики. Так, «конкретная кошка» отличается от «просто кошки» тем, что для придания смысла первому понятию требуется более длинная кинолента ситуаций, чем второму, строго говоря даже бесконечно длинная, ибо, имея в виду конкретную кошку, мы имеем в виду не только ее «личное дело», которое ведется со дня рождения, но и всю ее генеалогию. По своей природе «конкретные» и «абстрактные» понятия ничем принципиально не различаются, и те и другие отражают свойства реального мира. Если различие и есть, то оно противоположно тому, которое усматривает традиционная логика: абстрактные общие понятия чувственного и духовного опыта (не смешивать с конструктами
математики!) проще и ближе к природе, чем конкретные понятия, связанные с определенными предметами. Логиков ввело в заблуждение то обстоятельство, что в языке конкретные понятия появляются раньше, чем абстрактные. Но это как раз свидетельствует об их относительно более высоком положении в иерархии нейронных понятий-положений, благодаря которому они оказались на стыке с языковыми понятиями.
Платоновская теория идей, постулировав вымышленное идеальное бытие обобщенных предметов, поставила одноместные предикаты (свойства) в выделенное положение по сравнению с многоместными предикатами (отношениями), она придала свойствам статус истинного бытия, в котором отказала отношениям. Это со всей наглядностью проявилось в логике Аристотеля. Отсюда предметность и статичность мышления, столь характерная для греков классического периода. В следующей главе мы увидим, как этот образ мышления отразился на развитии математики.
1
Созвучие с русским не случайно, это древний индоевропейский корень (ср. лат. vidi
— увидел).
2
Для знакомых с математической логикой заметим: в широком смысле, включая правила вывода.
Подтверждение и отрицание
Эту схему мы измыслили чисто теоретически как простейший метод определения семантики языка в условиях, когда мозг представляется черным ящиком. И вот оказывается, что эта схема действительно существует в языковой деятельности, возникая стихийно на ранних этапах развития языка! У всех народов, во всех известных нам языках мы находим два эталонных действия, которые называются подтверждением и отрицанием. О глубокой древности этих действий свидетельствует то, что у подавляющего большинства народов (возможно, у всех) они выражаются не только в словах, но и в жестах. Если мы чуть-чуть приоткроем крышку черного ящика — в той степени, как это отражено на рис. 7.2, то сможем определить подтверждение как действие, которое производится, когда языковый объект и действительность находятся в отношении имя — значение (т. е. существует нужная ассоциация между языковыми и неязыковыми представлениями), а отрицание как действие, совершаемое, когда такого отношения нет. Но человек, когда он учится правильно употреблять положительные и отрицательные слова и жесты, разумеется, ничего не знает о представлениях, ассоциациях и т. п. Просто его сначала учат говорить «кошка», «собака» и т. д., указывая на соответствующие предметы, а потом учат совершать подтверждающие действия, когда говорят «это кошка», указывая на кошку, и отрицающее действие, когда говорят «это кошка», указывая на собаку. И на первом и на втором этапе человек обучается правильной языковой деятельности, опираясь на способность своего мозга к распознаванию и ассоциированию, но ничего не зная о механизмах мозга, т. е. используя его как черный ящик.
Последнее замечание объясняет, почему нет ничего удивительного в том, что схема эталонных действий прочно вошла в языковую практику. Мозг человека — черный ящик и для него самого, и для других членов общества. Отсюда потребность в общественно значимом способе уточнения семантики, которая проявляется, едва язык достигает минимального уровня сложности.
Эталонные действия подтверждения и отрицания относятся не к действительности самой по себе, подобно первичным языковым объектам, а к связи между первичными языковыми объектами и действительностью.
Они являются элементами метасистемы, по отношению к системе первичных языковых объектов. Введение в общественную практику действий подтверждения и отрицания — это начало того метасистемного перехода в рамках языковой деятельности, следующими этапами которого является появление языка логики и теории умозаключения. Подтверждения и отрицания появляются в развитии человеческой культуры весьма рано, но все же не столь рано, чтобы можно было найти их прообраз в действиях животных. Для первичных языковых объектов такие прообразы существуют, как мы знаем, в виде сигналов у животных. Среди этих сигналов бывают такие, которые можно описать как утвердительные и отрицательные, но они не имеют ничего общего с семантическими действиями подтверждения и отрицания, которые направлены на сами сигналы, закладывают основы метасистемы. Здесь мы видим еще одно проявление закона разрастания предпоследнего уровня. Огромный рост числа первичных языковых объектов (сигналов), который обнаруживается в человеческом обществе, начинается одновременно с зарождением метауровня.
Понятие понятия
Рассмотрим такую нервную сеть, которая на входе имеет много рецепторов, а на выходе — всего один эффектор, так что нервная сеть делит множество всех ситуаций на два подмножества: ситуации, вызывающие возбуждение эффектора, и ситуации, оставляющие его в покое. Задачу, решаемую в этом случае нервной сетью, называют задачей распознавания (имеется в виду распознавание принадлежности ситуации к тому или иному множеству). Животному в борьбе за существование приходится сплошь и рядом решать задачу распознавания, например: отличить ситуацию, опасную для жизни, от неопасной, отличить съедобные предметы от несъедобных и т. п. Это только наиболее яркие примеры, детальный анализ поведения животного приводит к выводу, что для выполнения сколь-нибудь сложного действия оно должно непрерывно решать множество «мелких» задач распознавания.
Множество ситуаций в кибернетике называют понятием1. Чтобы лучше уяснить, как кибернетическое понимание слова «понятие» связано с его обычным пониманием, допустим, что рецепторы рассматриваемой нами нервной сети — это светочувствительные нервные окончания сетчатки глаза или же вообще какие-то светочувствительные точки на экране, подающем информацию в нервную сеть. Рецепторы возбуждаются тогда, когда соответствующий участок экрана освещен (точнее, когда его освещенность больше некоторой пороговой величины), и остаются в состоянии покоя — в противном случае. Если на месте каждого возбужденного рецептора представить себе светлую точку, а на месте каждого невозбужденного — темную, то получится картина, которая отличается от изображения, падающего на экран, лишь своей дискретностью (т. е. тем, что она распадается на отдельные точки) и отсутствием полутонов. Будем считать, что точек (рецепторов) на экране достаточно много, а изображения, которые могут оказаться на экране, — их мы будем называть «картинками» — предельно контрастны, т. е. состоят лишь из белого и черного цвета. Тогда каждая ситуация соответствует определенной картинке.

Рис 2.1. Картинки, представляющие различные понятия
Согласно традиционной (аристотелевской) логике, когда мы думаем или говорим о какой-то определенной картинке (например, о той, которая находится в левом верхнем углу на рис. 2.1), то мы имеем дело с единичным понятием. Кроме единичных понятий, есть еще общие, или абстрактные, понятия. Например, мы можем думать о пятне вообще — не о каком-либо конкретном пятне (допустим, из числа изображенных в верхнем ряду на рис. 2.1), а о пятне как таковом. Точно так же мы можем обладать абстрактным понятием прямой линии, контура, четырехугольника, квадрата и т. д.2
Однако что значит «обладать абстрактным понятием»? Как можно проверить, обладает ли кто-то данным абстрактным понятием, например понятием «пятно»? Очевидно, только одним способом: предложить испытуемому серию картинок и попросить, чтобы он о каждой из них сказал, пятно это или нет. Если окажется, что он называет пятном только те и все те картинки, на которых «изображено пятно» (это уже с точки зрения испытующего), то, значит, понятием пятна он обладает. Иначе говоря, мы должны проверить его способность распознавать принадлежность любой предъявленной картинки к множеству картинок, которые мы описываем словом «пятно». Итак, абстрактное понятие в обычном смысле слова — во всяком случае когда речь идет о чувственно воспринимаемых образах — совпадает с введенным нами кибернетическим понятием понятия как множества ситуаций. Поэтому задачу распознавания называют также, желая сделать термин более конкретным, задачей распознавания образов (имеется в виду «обобщенных» образов) или задачей распознавания понятий (имеется в виду распознавание частных случаев понятий).
Множеству, состоящему из одной ситуации (картинки), соответствует в традиционной логике конкретное понятие «данная картинка». Отношения между множествами имеют свои непосредственные аналоги в отношениях между понятиями. Если большими буквами обозначить понятия, а маленькими — соответствующие множества, то дополнение множества a, т. е. множество всех мыслимых ситуаций, не входящих в a, соответствует понятию «не A».
Пересечение множеств a и b, т. е. множество ситуаций, которые входят и в a, и в b, соответствует понятию «A и B одновременно». Например, если A — понятие «прямоугольник», а B — понятие «ромб», то «A и B одновременно» — понятие «квадрат». Объединение множеств a и b, т. е. множество ситуаций, которые входят хотя бы в одно из множеств a и b, соответствует понятию «либо A, либо B, либо A и B». Если множество a включает в себя множество b, т. е. каждый элемент множества b входит в множество a, но не наоборот, то понятие B есть частный случай понятия A. При этом говорят, что понятие A более общее (абстрактное), чем понятие B, а понятие B более конкретное, чем A. Например, квадрат есть частный случай прямоугольника. Наконец, если множества a и b совпадают, то понятия A и B по существу тождественны и отличаются, быть может, лишь внешней формой их описания — способом распознавания. Встав на точку зрения кибернетики, т. е. отождествив понятие с множеством ситуаций, мы должны рассматривать перечисленные соответствия не как определение новых терминов, а просто как указание на наличие в нашем языке нескольких пар синонимов.
Понятия-конструкты
Понятия, подобные понятию «пространственное отношение», опираются на действительность не непосредственно, а через посредство промежуточных языковых построений, они становятся возможными в результате определенной языковой конструкции. Поэтому мы их будем называть конструктами. Высказывания, содержащие конструкты, требуют определенной языковой деятельности для установления своей истинности или ложности. Вне языковой системы понятия-конструкты не существуют. Например, понятие «пространственное отношение» не может возникнуть, пока нет слов «внутри», «между» и т. п., хотя соответствующие нейронные понятия уже давно бы и существовали.
Теперь мы можем сделать обзор уровней языка, рассматриваемого как иерархия по управлению. Сигналы животных примем за нулевой уровень языка. Появление эталонных действий подтверждения и отрицания, логических связок и предикатов является, как уже говорилось, метасистемным переходом. Он создает первый уровень языка. Следующий метасистемный переход образует второй уровень языка, понятия которого суть конструкты. Среди них находятся, в частности, понятия грамматики и логики; отличие от первого уровня состоит в том, что на первом уровне грамматика и логика появляются как высшие управляющие системы, которые создают язык, но сами еще не подвергаются управлению, на втором же уровне они становятся объектами изучения и управления (искусственного конструирования). Второй уровень языка можно назвать уровнем конструктов, а также уровнем самоописания.
Уровень развития языка определяет отношение языковой системы к нейронной системе. На нулевом уровне язык передает лишь элементарную управляющую информацию. На первом уровне он приобретает способность фиксировать и передавать некоторые модели действительности, но лишь те модели, которые уже существуют на нейронном уровне. Язык первого уровня можно представить в виде некоего слепка или снимка нейронных моделей (с учетом в качестве поправки обратного влияния языка). Наконец, на уровне конструктов язык получает возможность фиксировать модели действительности, которых не было и не могло быть (имея в виду данный биологический вид человека) на нейронном уровне.
Такие модели называют теориями.
Мы приводили числа и действия над ними в качестве простейшего и нагляднейшего примера моделей, не существующих на нейронном уровне и создаваемых на уровне языка. Арифметика — одна из первых теорий, созданных человеком. Легко видеть, что числа, точнее, большие числа, суть конструкты. Числам два и три соответствуют нейронные понятия: мы с одного взгляда отличаем два предмета от трех и от одного. Но число 137 — конструкт. Оно имеет смысл лишь постольку, поскольку имеет смысл число 136, которое в свою очередь опирается на число 135 и т. д.
Здесь есть один метасистемный переход — возникновение процесса счета, порождающего конкретные числа. В рамках метасистемы счета возникает иерархия по сложности — натуральный ряд чисел. Появление понятия «число» знаменует собой новый метасистемный переход, предполагающий, что счет прочно вошел в быт. Для того чтобы считать, абстрактного понятия числа не нужно, потребность в нем появляется лишь тогда, когда начинают рассуждать о счете. Понятие числа — это конструкт более высокого уровня, чем конкретные числа. На том же уровне находятся понятия арифметических действий.
Мы объединили во второй уровень языка все понятия, не опирающиеся непосредственно на нейронные понятия, а требующие вспомогательных языковых конструкций. При таком определении второй уровень является формально последним, но сам содержит иерархию по управлению, которая образуется путем метасистемных переходов и может в принципе быть сколь угодно высокой. Мы видели это на примере конкретных чисел и понятия «число». Язык второго уровня имеет сложную структуру, которую образно можно представить не в виде равномерных слоев, лежащих друг на друге, а в виде здания или комплекса зданий, имеющих и вертикальную, и горизонтальную структуру. Это следствие того, что метасистемный переход может иметь различный масштаб и происходить по отношению к различным подсистемам языка. Различные иерархии по управлению и порождаемые ими иерархии по сложности образуют, переплетаясь, многообразный архитектурный комплекс.Язык второго уровня — это язык философии и науки. Язык первого уровня называют обычно бытовым или разговорным.
Понятийные сваи
Информационная пропускная способность мозга несравненно больше, чем языка (в процессе речи). Язык не отражает всего богатства ощущений и сознательных представлений. Известно, например, что в древнегреческом языке одно слово обозначало и синий, и зеленый цвет, следовательно, вместо наших двух понятий у них было одно. Значит ли это, что они иначе воспринимали цвета? Конечно, нет. Человеческий глаз различает сотни цветовых оттенков, а слов для их обозначения существует совсем немного.
Первичные логические понятия можно сравнивать с колышками или, лучше, сваями, которые забивают в грунт нейронных понятий. Они проникают на небольшую глубину и занимают лишь небольшую часть площади. На этих сваях воздвигается этаж за этажом, целое здание — иерархия понятий языка. Мы гордимся зданием, потому что оно содержит понятия, которых не было в помине на уровне почвы — среди нейронных понятий. Но хорошо ли забиты сваи? Нельзя ли было забить их в других точках и не поздно ли еще забить дополнительные сваи? Как это повлияет на здание? Иначе говоря, является ли выбор первичных предикатов существенным для развития языка, культуры, мышления? Мы редко задаем себе этот вопрос, потому что не видим чистого грунта: он закрыт зданием языка. Но если спуститься под пол можно прикоснуться к первичному грунту и пошарить в темноте руками. При этом можно еще раз убедиться, как много грунта не затронуто сваями (особенно в сфере духовного опыта) и вспомнить слова Тютчева:
«Мысль изреченная есть ложь».
Из этого сравнения возникает еще один вопрос: сколь хороша архитектура здания? Является ли она единственно возможной, а если нет, то в какой степени выбор того или иного архитектурного проекта влияет на функционирование здания, на возможность его расширения, перестройки и т. п.? Иначе говоря, является ли грамматика языка (по крайней мере, в своих важнейших, принципиальных чертах) чем-то внешним и малозначительным для мышления или же она существенно влияет на мышление и направляет его развитие?
Оба эти вопроса — о влиянии выбора первичных предикатов и грамматики — сформулированы нами в виде, требующем ответа да или нет, лишь в целях ясности изложения. Дело, конечно, не в том, чтобы дать на них утвердительный или отрицательный ответ — он, в конце концов, всегда содержит элемент условности. Факт, что какое-то влияние есть, не вызывает сомнения, — задача в том, чтобы исследовать реальные данные о влиянии языка на мышление.
Позиционная система
Основы позиционной системы заложили вавилоняне. В системе счисления, которую они заимствовали от своих предшественников — шумерийцев, мы с самого начала (т. е. в древнейших дошедших до нас глиняных табличках, относящихся к началу третьего тысячелетия до н. э.), видим две основные «большие единицы» — десять и шестьдесят. Откуда взялось число шестьдесят — об этом можно только догадываться. Известный историк математики О. Нейгебауэр полагает, что источником послужило отношение между основными денежными единицами, имевшими хождение в Двуречье: одна мана (по гречески мина) составляла шестьдесят шекелей. Такое объяснение не удовлетворяет нашего любопытства, ибо тотчас же возникает вопрос: а почему в мане шестьдесят шекелей? Не потому ли как раз, что в ходу была шестидесятиричная система? Ведь не потому мы считаем десятками и сотнями, что в рубле сто копеек! Ассириолог Ф.Тюро-Данжен приводит лингвистические аргументы в пользу того, что система счета была первичным явлением, а система мер — вторичным. Выбор числа шестьдесят был, очевидно, исторической случайностью, однако вряд ли можно усомниться, что этой случайности способствовала важная особенность числа шестьдесят: оно имеет необычайно много делителей: 2, 3, 4, 5, 6, 10, 12, 15, 20, 30. Это свойство очень полезно и для денежной единицы (с тех пор как существуют деньги, существует и деление их поровну), и для основания системы счета, если предположить, что какой-то мудрец ввел ее, руководствуясь соображениями удобства вычислений.
Математическая культура вавилонян известна нам по текстам, относящимся к двум периодам: древневавилонскому (1800–1600 гг. до н. э.) и эпохе Селевкидов (305–64 гг. до н. э.). Сравнение их показывает, что в математике вавилонян каких-либо радикальных перемен за эти полтора тысячелетия не произошло.
Вавилоняне изображали единицу узким вертикальным клинышком



Таким образом, число 60 не только понималось как «большая единица», но и изображалось, в буквальном смысле слова, как большая единица. Соответственно появились «большие десятки» для десятикратно увеличенных больших единиц. Затем различие между большими и маленькими клиньями стерлось, они стали распознаваться по своему положению. Так возникла позиционная система. Число 747 = 12 × 60 + 27 вавилонянин записал бы в виде:


Сравнивая вавилонскую позиционную систему с современной, мы видим, что неопределенность в множителе 60 — результат отсутствия знака нуль, который мы приписали бы нужное число раз в конце целого числа или начале дробного. Другим результатом отсутствия нуля является еще более серьезная неопределенность в интерпретации числовой записи, которая соответствует тому случаю, когда мы ставим нули в промежуточных разрядах. В самом деле, как отличить в вавилонской записи число 3601 = 1 × 602 + 0 × 60 + 1 от числа 61 = 1 × 60 + 1? Оба эти числа изображаются двумя единицами. Иногда неопределенность такого рода устранялась путем отодвижения чисел друг от друга с оставлением свободного места для недостающего разряда. Но этот метод не применялся систематически и во многих случаях большой пробел между числами ничего не означал.
В астрономических таблицах эпохи Селевкидов встречается обозначение отсутствующего разряда с помощью знака, аналогичного нашей точке (разделитель фраз). В древневавилонскую эпоху ничего подобного мы не находим. Как же умудрялись древние вавилоняне избегать путаницы?
Полагают1, что разгадка состоит в следующем.
Ранние математические тексты вавилонян, дошедшие до нас, представляют собой сборники задач и их решений, созданные несомненно как учебные пособия. Их цель — обучить практическим приемам решения задач. Но ни в одном из текстов не описывается, как производить арифметические действия, в частности такие сложные для своего времени, как умножение и деление. Следовательно, предполагалось, что ученики каким-то образом умеют это делать. Так как совершенно невероятно, чтобы вычисления производились в уме, естественно предположить, что вавилоняне пользовались каким-то счетным прибором типа абака. На абаке числа выступают в своем натуральном, стихийно позиционном виде, а специальный знак для нуля не нужен, ибо бороздка, соответствующая пустому разряду, просто остается без камешков. Представление числа на абаке было основной формой задания числа, и в этом представлении не было никакой неопределенности. Числа, которые приводятся в клинописных математических текстах, играют роль поэтапных ответов, призванных контролировать правильность хода решения. Ученик делал выкладки на абаке и сверялся с глиняной табличкой. Ясно, что такому контролю отсутствие знака для пустых разрядов нисколько не препятствовало. Когда распространились объемистые астрономические таблицы, служащие уже не для контроля, а в качестве единственного источника данных, стали употреблять и разделительный знак для обозначения пустых разрядов. Однако свой «нуль» вавилоняне никогда не ставили в конце числа: очевидно, они его воспринимали именно как разделитель, но не как полноправное число.
Познакомившись с египетской и вавилонской системами записи дробей и действий над ними, греки для астрономических вычислений выбрали вавилонскую, ибо она была несравненно лучше.
Но в записи целых чисел они сохранили свою алфавитную систему. Таким образом, греческая система, употреблявшаяся в астрономии, оказалась смешанной: целая часть числа изображалась в десятичной непозиционной системе, дробная часть — шестидесятиричной позиционной.
Не слишком логичное решение для создателей логики! С их легкой руки мы и до сих пор считаем часы и градусы (угловые) десятками и сотнями, а делим их на минуты и секунды.
Зато греки ввели в позиционную систему современный знак 0 — нуль, произведя его, как полагает большинство специалистов, от первой буквы слова ????? — «ничто». При записи целых чисел (кроме числа 0) этот знак, естественно, не находил применения, ибо алфавитная система, которой пользовались греки, не была позиционной.
Современную систему записи чисел изобрели индийцы в начале VI в.н.э. Вавилонский позиционный принцип и греческий знак нуль для обозначения пустоты они применили не к основанию 60, а к основанию 10. Система получилась и последовательной, и экономной, и не противоречащей традиции, и чрезвычайно удобной для вычислений.
Индийцы передали свою систему арабам. В Европе позиционная система счисления появилась в XVI в. с переводом знаменитой арабской арифметики ал-Хорезми (ал-Хваризми). Она вступила в жестокую борьбу с традиционной римской системой и в конце концов одержала победу. Однако еще в XVI в. в Германии был издан и выдержал много изданий учебник арифметики, в котором используются исключительно «немецкие», т. е. римские цифры, или, лучше сказать, числа, так как в то время цифрами называли только знаки индийской системы. В предисловии автор пишет: «Я изложил эту счетную книгу обычными немецкими числами на благо и пользу непосвященному читателю (которому сразу трудно будет выучить цифры)». Десятичные дроби в Европе стали употреблять начиная с Симона Стевина (1548–1620).
Познание мира
Что такое знание? Как можно с кибернетической точки зрения описать ту ситуацию, когда человек или животное знает то-то и то-то?
Допустим, вы знаете, что в соседней комнате находятся два человека. Тот факт, что они там действительно находятся, означает, что если вы войдете в комнату, то увидите там двух людей. Тот факт, что вы знаете об этом, означает, что, не входя в комнату реально, а лишь представив, как вы открываете дверь и входите в комнату, вы представляете себе и двух людей, находящихся в комнате. Следовательно, в вашем мозгу имеет место ассоциация представлений, позволяющая вам предвидеть результаты некоторых действий, т. е. некоторая модель действительности. Так же интерпретируются утверждения, что, видя катящееся колесо, вы знаете, где оно будет через секунду; что собака, на которую замахиваются палкой, знает, что последует удар, и т.п. Знание — это наличие в мозгу какой-то модели действительности. Увеличение знания, т. е. возникновение новых моделей действительности в мозгу, — это процесс познания. Познание мира не есть привилегия человека, оно свойственно уже высшим животным. Пятый этап эволюции можно назвать этапом индивидуального познания мира.
|
|