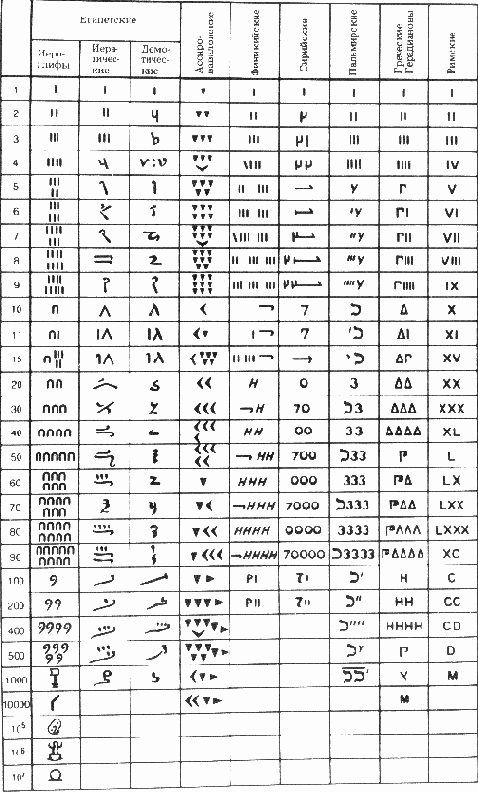
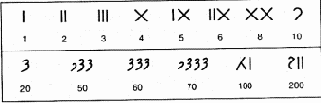
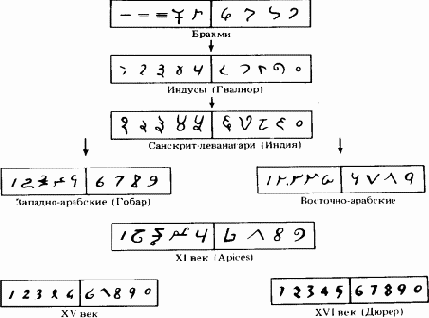
Познания древних в геометрии
Что же знали египтяне из геометрии? — Правильные формулы для площади треугольника, прямоугольника, трапеции. Площадь неправильного четырехугольника, как можно судить по одному сохранившемуся документу, вычислялась так: полусумма двух противолежащих сторон умножалась на полусумму двух других противолежащих сторон. Формула эта грубо неверна (за исключением того случая, когда четырехугольник прямоугольный и когда она не нужна). Ни в каком разумном смысле ее нельзя назвать даже приближенной. Это, по-видимому, первый зафиксированный историей пример утверждения, которое выводится не из сравнения с опытными данными, а из «общих соображений». Площадь круга египтяне вычисляли, возводя в квадрат 8/9 его диаметра. Это соответствует приближенному значению числа ?, отличающемуся примерно на 1% от истинного значения.
Объемы параллелепипедов и цилиндров вычислялись умножением площади основания на высоту. Высшим из известных нам достижений египетской геометрии является правильное вычисление объема усеченной пирамиды с квадратным основанием (Московский папирус). Оно следует формуле
V = (a2 + ab + b2) × h/3,
где h — высота, a и b — стороны верхнего и нижнего основания.
Наши сведения о познаниях древних вавилонян в математике скудны и отрывочны, но общее представление по ним все-таки составить можно.
Совершенно точно известно, что вавилоняне знали «теорему Пифагора», т. е., конечно, не теорему, а самый факт, что сумма квадратов катетов равна квадрату гипотенузы. Как и египтяне, они правильно вычисляли площади треугольников и трапеций. Длину окружности и площадь круга они вычисляли, пользуясь значением ? = 3, что гораздо хуже, чем египетское приближение. Объем усеченной пирамиды или конуса вавилоняне вычисляли, умножая полусумму площадей оснований на высоту (неверная формула).
Предикаты
Конструкция, сопоставляющая нескольким объектам высказывание, называется предикатом. Предикаты делятся на одноместные, двухместные, трехместные и т.д. в соответствии с числом объектов, которого они требуют. Для записи их используют функциональные обозначения. Предикат можно записать в виде функции с незаполненными местами для аргументов, например
P( ), L( , ), I( , , )
или же в виде
P(x), L(z, y), I(x, y, z)
оговорив, что x, y, z — предметные переменные, т. е. символы, которые в конечном счете должны быть заменены на объекты, но какие — пока неизвестно. Впрочем, вторая форма изображает, строго говоря, уже не предикат, а высказывание, содержащее предметные переменные. Вместо больших букв мы будем также использовать словосочетания в кавычках, например,
«красный»(x), «между»(x, у, z)
и специальные математические знаки, например,
<(х, у).
Одноместный предикат выражает свойство объекта, предикат более чем с одним аргументом — отношение между объектами. Если места для аргументов в предикате заполнены, то мы имеем дело с высказыванием, утверждающим наличие данного свойства или отношения. Высказывание
«красный»(«мяч»)
означает, что «мяч» обладает свойством «красный». Конструкция
<(a, b)
равнозначна соотношению (неравенству) a < b.
Соединяя предикатные конструкции логическими связками, мы получаем более сложные высказывания. Например, соотношение |z| > 1, которое мы раньше записывали, не расчленяя высказываний на элементы, мы запишем теперь в виде
>(z, 1) ? <(z, -1).
Русское издание этой книги выходит
Русское издание этой книги выходит через двадцать с лишним лет после ее написания. За это время наука существенно продвинулась вперед. Достаточно вспомнить раскрытие генетического кода, открытия в астрофизике, новую теорию элементарных частиц. Персональные компьютеры вошли чуть ли не в каждый дом. Между тем книга выходит в том виде, в каком она была подготовлена к печати в 1970 г. Если бы я стал что-то добавлять к ней, то это превратилось бы, в конечном счете, в написание новой книги, гораздо большей по объему, и она включала бы в себя старую практически целиком и без перемен. Ибо основная тема книги — Эволюция Вселенной как последовательность метасистемных переходов — не пострадала от времени. Напротив, появились новые указания на плодотворность этого подхода. В настоящее время мы с группой коллег начали работу над проектом PRINCIPIA CYBERNETICA, который включает дальнейшее развитие этих идей. Некоторое представление об этом проекте дает написанная мною совместно с Клиффом Джослиным статья “Кибернетический манифест”. Эта статья также включает краткое изложение основных идей книги и включена в качестве приложения к настоящему изданию.
“Феномен науки” вышел в английском и японском переводах. Я очень рад, что он может, наконец, выйти и в русском оригинале.
Одно место в “Феномене науки” требует комментария в свете последних достижений физики. В разделе “Сумасшедшие теории и метанаука” я высказал мысль, что для того, чтобы разрешить трудности в современной теории элементарных частиц, надо разработать методы “метанауки”, т. е. теории о том, как строить теории. Причину я усматривал в том, что основные понятия физики на ранних стадиях ее развития брались из нашей интуиции макроскопического мира. Но для познания законов микромира (а точнее, для построения математических моделей этого мира) наша “макроскопическая” интуиция неадекватна. Если интуиция не дает нам впрямую тех “колесиков”, из которых можно строить модели микромира, то нам нужны какие-то теории о том, как эти колесики выбирать и как модели строить. Это и будет метанаука.
С тех пор как была написана моя книга, физика элементарных частиц сделала огромный шаг вперед — и без всякой метанауки, а лишь на основе старой идеи, что одни частицы могут как бы состоять из других, более элементарных частиц. Тем не менее я полагаю, что моя логика остается в силе, и если не на данной, то на какой-то последующей стадии развития точных наук метатеоретические методы докажут свою плодовитость.
В.Ф.Турчин
Обнинск, август 1990 г.
популярной литературы совсем немного книг,
Среди огромной массы научной и научно- популярной литературы совсем немного книг, которые можно считать вехами на пути человечества в формировании целостного и оптимистического мировоззрения, т.е. книг философских в истинном смысле этого слова. Книга, которую держит в руках читатель, несомненно, принадлежит к этой редкой категории. И это не случайно, так как ее автор являет собой редкий тип ученого-естественника, который философствует не потому, что это модно, престижно или, скажем, принято. Он философствует для того, чтобы привести в прямое соответствие философские знания и практику собственной жизни.
Автор излагает оригинальную теорию эволюции, базируясь на современных кибернетических концепциях и на одной основной идее, а именно — идее метасистемного перехода как кванта эволюции. Внешне все очень просто. Если у вас есть некоторая исходная кибернетическая система (амеба, человек, общество и т.п.), то метасистемный переход — это переход к некоторой другой системе, включающей в себя множество систем типа исходной. По сути здесь всегда возникает новый уровень управления. Примеры: переход от простейших одноклеточных организмов к многоклеточным, возникновение нервной системы, мозга, речи и т.д.
Но заслуга автора не ограничивается тем, что он высказывает идею метасистемного перехода как кванта эволюции. Он прослеживает с позиции этой идеи эволюцию на Земле от простейших макромолекул до современной науки (математики, философии) и культуры. Делает он это столь ярко и интересно, что не остается никаких сомнений в огромной мощности исходной идеи. По сути своей “Феномен науки” — глубокая научно-философская книга, но написана она как роман и, чтобы прочесть ее, достаточно любопытства и знаний в объеме средней школы.
Читатель, который возьмет на себя труд последовать за автором, узнает массу интереснейших вещей. Он, в частности, узнает, каким видится мир глазами лягушки, чем же все-таки (одним и принципиальным) отличается мышление животного (собаки, обезьяны) от мышления человека, что должно было произойти в мышлении человека, чтобы оно из “примитивного” стало “современным”, что такое юмор и на какой стадии эволюции он возникает, что такое научная теория и чем отличается “хорошая” теория от “плохой”, много ли на самом деле зависит от простого человека (“винтика”) в обществе, что есть Добро, Высшее благо и Высшая цель, и еще многое другое.
Сказанного, думаю, достаточно, чтобы читатель получил представление о предмете и характере книги. Углубляться в детали нет смысла, так как при этом пришлось бы невольно и безнадежно конкурировать с авторским текстом, одновременно паразитируя на нем. Поэтому будем считать своей дальнейшей задачей — рассказать немного об авторе и коротко осветить историю его диссидентства. Ведь когда писалась книга, В.Ф.Турчин был советским гражданином, а с октября 1977 г. он живет в Америке, работает профессором в области компьютерных наук в Нью-Йоркском городском университете и в 1982 г. получил гражданство США.
В.Ф.Турчин родился в 1931 г. в Москве. Окончил физический факультет МГУ и с 1953 по 1964 г. работал под Москвой в Обнинске в Физико-энергетическом институте, где изучал рассеяние медленных нейтронов в жидкостях и твердых телах и защитил докторскую диссертацию. В 33 года он уже был известным физиком-теоретиком с большими перспективами.
И тем не менее в 1964 г. В.Ф.Турчин оставляет физику, переходит в Институт прикладной математики АН СССР (ныне Институт им. М.В.Келдыша) и погружается в информатику. Намек на причину такой рискованной смены среды содержит предпоследний абзац следующего далее авторского предисловия. Он оставил науку ради метанауки.
В информатике, как и в физике, ему сопутствует успех. Он создает новый язык программирования — язык Рефал, на котором удобно описываются алгоритмические языки, трансляторы, символьные математические преобразования и многое другое. Более того, вокруг В.Ф.Турчина складывается неформальная научная школа — научное направление, которое живет и успешно развивается до сих пор, даже после отъезда, а точнее изгнания его лидера из СССР.
Читатель уже мог догадаться, что человек с таким научно-философским диапазоном, как В.Ф.Турчин, обычно имеет четкую точку зрения на социально-политические процессы в мире и тем более в своей стране. К чести В.Ф.Турчина, он не только имел такую точку зрения, но и не боялся ее высказывать.
В 1968 г. он написал статью “Инерция страха” и предложил ее для публикации журналу “Коммунист”. В ней, в частности, доказывалось, что тоталитарное общество обречено, и предлагался вариант перехода от тоталитарного общества к свободному. (Корни перестройки, как видите, можно обнаружить много раньше 80-х годов.) Статья не была напечатана, но естественно имела “последствия” для ее автора. Небольшое количество экземпляров ходило в “самиздате”; в 1976 г. статья была переработана в солидную книгу “Инерция страха. Социализм и тоталитаризм”, которая годом позже была опубликована в США на русском, а затем и на английском языках.
Одним из первых читателей “Инерции страха” был А.Д.Сахаров. С 1968 г. общественная деятельность этих людей протекала совместно. Именно по инициативе В.Ф.Турчина в 1970 г. было написано и направлено в правительство письмо, о котором рассказал А.Д.Сахаров в своих воспоминаниях. В письме обращалось внимание на необходимость либерализации и демократизации общества, поскольку без этого экономике страны угрожает полный крах.
Но вернемся к книге “Феномен науки”. Она была написана в 1970 г. по договору с издательством “Советская Россия”. Хотя она и собрала самые положительные рецензии, три года тянулась волокита с ее набором. В редакции “не понимали”, как можно положить на стол главного редактора книгу с такой последней главой. Слишком очевидным было противоречие духу марксистско-ленинской философии. И все же к 1973 г. книга была набрана и прошла стадию верстки. До выхода в свет оставалось совсем немного, но... началась кампания против А.Д.Сахарова. В центральной прессе публикуется открытое письмо, клеймящее его позором, за подписями 40 членов Академии наук... В.Ф.Турчин выступает на пресс-конференции перед иностранными корреспондентами в защиту А.Д.Сахарова. Вскоре после этого ему звонят и, извиняясь, объясняют, что в типографии то ли рухнула штукатурка с потолка, то ли рухнул весь потолок как раз на набор книги, то ли сам набор рухнул с полки на пол, но восстановить его нет никакой возможности.
Вот некоторые обстоятельства, проливающие свет на то, почему переводы книги на английский и японский языки вышли много раньше русского оригинала.
В начале 1973 г. В.Ф.Турчин переходит в ЦНИПИАС (Центральный научно-исследовательский проектный институт автоматизации в строительстве) на должность заведующего лабораторией. Здесь сыграли роль два соображения. Во-первых, он считал свое новое место работы менее режимным и, следовательно, более совместимым с теми контактами, которые неизбежно возникали в связи с его правозащитной деятельностью. Во-вторых, в ЦНИПИАС были обещаны более широкие возможности для организационного оформления научной школы В.Ф.Турчина.
В апреле 1974 г. В.Ф.Турчин становится председателем московского отделения Amnesty International — группы “Международная амнистия”, выступающей в защиту узников совести во всех странах независимо от их политической системы. В том же 1974 г. ученый совет ЦНИПИАС не переаттестовывает его в должности, после чего его “клеймят позором” на собрании сотрудников и увольняют. Все дальнейшие попытки получить хоть какую-нибудь работу были тщетны. Семья с двумя сыновьями оказалась на зарплате жены Т.И.Турчиной — младшего научного сотрудника института Нефтехимсинтеза им. Губкина.
В декабре 1976 г. В.Ф.Турчин получает “последнее предупреждение” от КГБ: либо он уезжает, либо его ждет арест. Обыск и допросы к тому времени он уже прошел. В 1977 г. начались аресты членов Хельсинкской группы: Ю.Орлова, А.Гинзбурга, А.Щаранского и др. Хотя В.Ф.Турчин и не был формально членом Хельсинкской группы, но готовил материалы для нее и участвовал в пресс-конференции Хельсинкской группы в качестве представителя Международной амнистии. Пришлось делать “выбор”. Кто был близко знаком с В.Ф.Турчиным, знает, как он не хотел уезжать. Вот вкратце те обстоятельства, при которых наша наука потеряла Турчина, а американская — нашла.
Для полноты картины следует еще сказать, что В.Ф.Турчин — веселый, жизнерадостный, остроумный человек, блестящий рассказчик.
Общение с ним — это всегда радость. Он был капитаном команды КВН города Обнинска в 1963 г., когда КВН только начинался. Команда под его водительством победила команду из Дубны! Он же был одним из составителей сборников “Физики шутят” и “Физики продолжают шутить”, доставляющих своим читателям много веселых минут и ставших давно библиографической редкостью.
Читатель! Вас ждет встреча с весьма неординарным автором, ученым и гражданином. Счастливого пути!
В заключение хочу выразить благодарность всем, кто содействовал изданию книги. Особую благодарность я выражаю нескольким людям. А.Б.Ходулев установил на компьютере и настроил систему LATEX, которой я пользовался при подготовке оригинал-макета книги. Он же был моим учителем по системе и безотказным консультантом. Т.Н.Малышева и Н.Б.Дзалаева взяли на себя очень большую работу по первоначальному вводу в компьютер текста книги (в системе LEXICON). Самую разнообразную помощь я получал от Анд.В.Климова, который, в частности, отлично выполнял функции “канала связи” с “удаленным” автором.
Коллега В.Ф.Турчина
по Институту прикладной математики
В.С.Штаркман
февраль 1992 г.
Представления
Редупликация различных подсистем нервной сети может породить множество различных групп классификаторов, «повисающих в воздухе». Среди них могут появиться дубликаты целых этажей иерархии, состояния которых в точности соответствуют состоянию тех «осведомленных» классификаторов, которые получают информацию от рецепторов. Соответствуют, но не совпадают. Это мы видим на примере нейронов A и Z на рис. 2.9,к. В сложных системах неосведомленные дубликаты осведомленных классификаторов могут хранить большое количество информации. Состояния этих дубликатов мы будем называть представлениями, отдавая себе ясный отчет, что тем самым мы даем определенную кибернетическую интерпретацию этому психологическому понятию. Очевидно, имеет место тесная связь между представлениями и ситуациями, которые ведь суть не что иное, как состояния аналогичных классификаторов, но получающих информацию от рецепторов. Цель представляет собой частный случай представления, а точнее тот случай, когда сравнение постоянного представления и меняющейся ситуации используется для выработки действия, сближающего их друг с другом. Описанное выше гипотетическое животное обожает температуру 16?, и «светлый образ» этой блаженной ситуации, которая есть определенная частота импульсов нейрона A, живет в ее памяти в виде точно такой же частоты импульсов нейрона Z.
Это очень примитивное представление. Чем выше организована «осведомленная» часть нервной системы, тем сложнее и ее дубликаты (мы будем их называть фиксаторами представлений) и тем разнообразнее представления. Так как классификаторы могут принадлежать к разным уровням иерархии и ситуация может быть выражена в разных системах понятий, представления также могут различаться своим «понятийным языком», ибо они могут быть состояниями фиксаторов разных уровней. Далее, степень устойчивости состояний фиксаторов представлений также может быть весьма различной. Поэтому представления сильно отличаются по своей конкретности и стабильности. Они могут быть точными и конкретными, почти чувственно воспринимаемыми. Крайним случаем здесь является галлюцинация, которая субъективно воспринимается как реальность и на которую организм реагирует так же, как на соответствующую ситуацию. С другой стороны, представления могут быть очень приблизительными как из-за своей неустойчивости, так и из-за своей абстрактности. Последний случай часто встречается в художественном и научном творчестве, когда представления выступают как цель деятельности. Человек смутно чувствует, что ему надо, и пытается воплотить это в твердой предметной форме. У него долго ничего не получается, потому что его представления не обладают необходимой конкретностью. Однако в один прекрасный момент (и это действительно прекрасный момент!) он вдруг добивается своей цели и ясно осознает, что он сделал именно то, что хотел.
Прикладная арифметика
Магистральный путь к современной науке лежит через культуру древней Греции, которая наследовала достижения египтян и вавилонян. Остальные влияния и связи (в частности, передаточная функция, выполненная арабами) были более или менее существенны, но решающего значения, по-видимому, не имели. Истоки египетской и шумеро-вавилонской цивилизаций теряются во мраке первобытных культур. Поэтому в нашем обзоре истории науки мы ограничимся этими тремя культурами древности.
О записи чисел египтянами и вавилонянами мы уже говорили. Надо только добавить несколько слов о том, как египтяне записывали дроби. Система их была с современной точки зрения чрезвычайно оригинальна и столь же неудобна. Египтяне имели специальную форму записи только для так называемых основных дробей, т. е. полученных делением единицы на целое число, и еще двух простых дробей, имевших с древних времен особые иероглифы, а именно 2/3 и 3/4. Впрочем в позднейших папирусах особое обозначение для 3/4 исчезло. Чтобы записать основную дробь, надо было над обычным числом поставить знак


Остальные дроби египтяне разлагали на сумму нескольких основных дробей. Например, 3/8 записывалось как 1/4 + 1/8, а 2/7 в виде 1/4 + 1/28. Для результата деления 2 на 29 египетская таблица давала разложение 2/29 = 1/24 + 1/58 + 1/174 + 1/232.
На технике счета египтян и вавилонян мы останавливаться не будем. Достаточно сказать, что те и другие умели производить четыре действия арифметики над всеми числами (целыми, дробными или смешанными), которые встречались им на практике. Для действий с дробями они пользовались вспомогательными математическими таблицами; это таблицы обратных чисел у вавилонян и таблицы основных дробей — у египтян. Египтяне записывали промежуточные результаты на папирусе, вавилоняне, по-видимому, выполняли действия на абаке, поэтому детали их техники остались неизвестными.
Что же считали древние математики? Есть один отрывок из египетского папируса времен Нового Царства (1500–500 гг.
до н. э.), в котором очень образно и с большой дозой юмора описывается деятельность царских писцов и который по этой причине неизменно приводится во всех книгах по истории математики. Не избежим и мы этой участи. Вот этот отрывок2:
Я хочу объяснить тебе, что это такое, когда ты говоришь: «Я, писец, дающий приказы армии»... Я ставлю тебя в тупик, когда приношу тебе повеление от твоего господина, тебе — его царскому писцу... мудрому писцу, поставленному во главе этого войска. Надо сделать наклонную насыпь в 730 локтей длины и 55 локтей ширины; она состоит из 120 отдельных ящиков и покрывается перекладинами и тростником. На верхнем конце она имеет высоту в 60 локтей, а в середине — 30 локтей. Уклон ее дважды по 15 локтей, а настил 5 локтей. Спрашивают у военачальников, сколько понадобится кирпичей, и у всех писцов, и ни один ничего не знает. Все они надеются на тебя и говорят: «Ты искусный писец, мой друг, сосчитай это для нас поскорей. Имя твое славится»... Сколько же нужно кирпичей?
Текст этот, несмотря на свою популярность, не слишком вразумителен. Однако, как бы мы его ни толковали, он дает представление о тех задачах, которые приходилось решать египетским писцам. Мы видим, в частности, что они должны были уметь вычислять (сколь верно — это другой вопрос) площади и объемы. И действительно, египтяне обладали некоторыми познаниями в геометрии. Эти познания, по весьма обоснованному мнению древних греков, возникли в самом Египте. Один из философов школы Аристотеля начинает свое сочинение словами3:
Так как нам необходимо здесь обозреть начало наук и искусств, то мы сообщаем, что геометрия, по свидетельству весьма многих, была открыта египтянами и возникла при измерении Земли. Это измерение было необходимо вследствие разлития реки Нила, постоянно смывавшего границы. Нет ничего удивительного, что эта наука, как и другие, возникла из потребностей человека. Всякое возникающее знание из несовершенного переходит в совершенное. Зарождаясь путем чувственного восприятия, оно постоянно становится предметом нашего рассмотрения и, наконец, делается достоянием нашего разума.
Деление знания на несовершенное и совершенное и определенная извинительная интонация по поводу «низкого» происхождения науки — это, конечно, от греческого философа. Египтяне, как и вавилоняне, не знали ничего подобного. Для них знание было чем-то вполне однородным. Они умели делать геометрические построения и знали формулы для площади треугольника и круга, как умели стрелять из лука и знали свойства целебных трав и даты разлива Нила. Геометрии как искусства выводить «истинные» формулы у них не было, она существовала, по выражению Б. Ван дер Вардена, лишь как раздел прикладной арифметики. Очевидно, при получении формул они использовали некоторые наводящие соображения, однако эти соображения мало кого интересовали. На отношение к формуле они не влияли.
Проблема Высшего Блага
Как и когда возникает проблема Высшего Блага и Высшей Цели? Очевидно, у животных ее не было. Не было ее и на ранних этапах развития человеческого общества. До поры до времени для человека, как и для животного, благом является то, что доставляет удовольствие, и иерархии удовольствий соответствует иерархия целей, вершину которой образуют инстинкты сохранения жизни и продолжения рода. Понятие цели и понятие блага вообще неотделимы друг от друга, это два аспекта одного понятия. Человек стремится к благу по определению и называет благом то, к чему он стремится. На стадии, когда благо отождествляется с удовольствием, человек в нравственном отношении ничем не отличается от животного, нравственных проблем для него не существует. И здесь дело не в природе удовольствия, а в его заданности, в том, что критерий удовольствия есть высшая управляющая система, которая меняет цели, сама не испытывая изменений. Уже с чисто биологической точки зрения удовольствия человека отличаются от удовольствий животных — вспомним, например, о чувстве прекрасного, а по мере усложнения социальной структуры человек приобретает новые удовольствия, которые незнакомы животным. Тем не менее, проблемы Высшего Блага это не создает. Она возникает тогда, когда культура начинает решительно влиять на систему удовольствий, когда оказывается, что то, что люди думают, говорят и делают, способно настолько сильно изменить их отношение к миру, что события, вызывающие ранее удовольствие, вызывают теперь неудовольствие, и наоборот. Правда, удовольствия низшего уровня (от непосредственного удовлетворения физических потребностей) практически не меняются с культурой, но удовольствия высшего уровня (например, упоение своим охотничьим искусством, выносливость и т. п.) оказываются способными перевесить неудовольствия низшего уровня. Таким образом, критерий удовольствия сам оказывается подверженным управлению. Происходит метасистемный переход — возникают социальная шкала ценностей и система норм поведения.
Но это еще только введение, пролог к проблеме Высшего Блага.
В первобытном обществе нормы поведения можно сравнить с инстинктами животных; в общественном сверхмозге они и представляют собой точный аналог инстинктов животного индивидуума, заложенных в его мозге. Управление ассоциациями (мышление) разрушает инстинкты или, лучше сказать, понижает их в должности и заменяет их социальными нормами поведения. В первобытном обществе они — такой же абсолют, как для животного — инстинкты. Они хотя и меняются в процессе развития общества, но неосознанно, как и инстинкты в процессе эволюции вида. Каждым индивидуумом они воспринимаются как нечто данное и несомненное. Но вот происходит еще один метасистемный переход — к практическому мышлению — и тогда-то проблема Высшего Блага встает во весь рост.
Теперь люди не только воздействуют своей языковой деятельностью на свои собственные критерии удовольствия, но и осознают это воздействие. Простое и ясное «Я так хочу!» теряет свою первичность, свою данность. Когда человек сознает, что то, чего он хочет, есть результат его воспитания, воздействия со стороны других людей, а теперь зависит и от него самого, может быть изменено путем размышления и самовоспитания, он не может не задавать себе вопроса: а чего же он должен хотеть? Он обнаруживает в своем сознании пустоту, которую надо чем-то заполнить. Существует ли абсолютное Высшее Благо, к которому надо стремиться? — спрашивает он себя. Как жить? Каков смысл жизни?
Но однозначных ответов на эти вопросы он получить не может. Цель можно вывести только из цели. И если человек волен в своих желаниях, то он волен и в желаниях желаний. Круг сомнений и вопросов замыкается, и опереться больше не на что. Система поведения повисает в воздухе. Наивные первобытные верования и традиционные нормы поведения рушатся. Наступает эпоха религиозных и этических учений.
Этих учений много, и во многом они различны, но в то же время, как оказывается, есть у них и много общего — во всяком случае, если говорить об учениях, получивших широкое распространение. Теперь наша задача — уяснить, приводит ли научное мировоззрение к какому-либо определенному этическому учению и если да, то к какому именно.Заодно мы обсудим вопрос о природе общего знаменателя различных этических учений.
Продолжение мозга
Допустим, что в пещеру входят три врага, а выходят два. Тут первобытный человек и без помощи пальцев сообразит, что один враг остался в пещере. Это работает модель, которая есть у него в мозгу. А если входят двадцать пять, а выходят двадцать четыре или двадцать три? Здесь человеческий мозг окажется бессилен: он не содержит нужной модели, нужных понятий. Мы мгновенно и безошибочно различаем множества из одного, двух, трех, четырех предметов и можем отчетливо представить их в своем воображении. Эти понятия даны нам от природы, они распознаются нейронной сетью мозга, подобно понятиям пятна, линии, соприкасания и т. п. С понятиями, которые выражаются числами от пяти до восьми, дело обстоит хуже: здесь многое зависит от индивидуальных особенностей и тренировки. Что же касается понятий «девять», «десять» и т. д., то, за редчайшими исключениями, которые рассматриваются как отклонения от нормы, все они сливаются в одно понятие «много». И тогда человек создает язык, материальный носитель которого (например, пальцы) служит фиксатором новых понятий, выполняя функции тех классификаторов, для которых не нашлось места в мозгу. Если не хватит пальцев, пойдут в ход камешки, палочки, зарубки, а в более развитых языках — цифры и наборы цифр. Какой используется язык — неважно, важно лишь умение кодировать. Процесс счета служит для распознавания новых понятий, выполняя функции нервной сети, работа которой приводит в возбужденное состояние тот или иной классификатор. В результате счета объекту R, например отряду врагов, сопоставляется объект L, например ряд зарубок или цифр. Наконец, правила действий над объектами языка и связи между ними (например, типа 6 + 3 = 9 и т. п.) соответствуют ассоциациям между понятиями в мозгу. Это завершает аналогию между моделями, реализуемыми с помощью языка, и моделями, которые создаются нейронными сетями мозга.
Если орудие — продолжение руки человека, то язык — продолжение его мозга. Он служит для той же цели, для которой служит мозг: увеличению жизнеспособности вида путем создания модели окружающей среды.
Он продолжает дело мозга с помощью материала, лежащего за пределами физического тела человека, основываясь на моделях (понятиях и ассоциациях) доязыкового периода, реализуемых нервными сетями. Человек как бы перешагнул через границу своего мозга. Возможности такого перехода (а именно установления связи между внутренним и внешним материалом) открылись благодаря способности управлять ассоциированном, выразившейся в языкотворчестве.
Две функции языка: коммуникативная и моделирующая — неразрывно связаны друг с другом. Счет на пальцах мы привели в качестве примера модели, которая возникает только благодаря языку и которая не может существовать без языка. При коммуникативном использовании языка он выполняет более скромную задачу: фиксирует модель, которая уже существует в чьем-то мозгу. Такие фразы, как «идет дождь», «в соседнем лесу волки» или более отвлеченные: «гадюка ядовита», «огонь гасит воду», суть модели действительности. Когда один человек сообщает это другому, ассоциации, которые раньше были только в голове первого, утверждаются в голове второго.
Благодаря наличию языка человеческое общество коренным образом отличается от сообщества животных. В животном мире члены сообщества контактируют лишь на уровне функций, связанных с питанием и размножением. Члены человеческого общества контактируют не только на этом уровне, но и на самом высоком уровне их индивидуальной организации — на уровне моделирования внешнего мира с помощью ассоциации представлений. Люди, так сказать, контактируют мозгами. Язык — это не только продолжение каждого индивидуального мозга, но и общее, единое продолжение мозгов всех членов общества. Это коллективная модель действительности, над совершенствованием которой трудятся все члены общества и которая хранит опыт предыдущих поколений.
Промышленные революции
Следующий качественный скачок в системе производства — использование новых источников энергии, кроме мускульной энергии человека и животных. Это, конечно, тоже метасистемный переход, ибо возникает новый уровень системы — уровень двигателей, управляющий перемещением рабочих частей машины. Происходит первая промышленная революция (XVIII в. н. э.), радикально меняющая весь облик производства. Лейтмотивом технического прогресса становится совершенствование двигателей. Сначала это паровая машина, затем двигатель внутреннего сгорания, затем электромотор. Вслед за веком материала наступает век энергии. Наконец, наше время является свидетелем еще одного метасистемного перехода в структуре производства. Возникает новый уровень — уровень управления двигателями. Начинается вторая промышленная революция, которая, очевидно, в еще большей степени, чем первая, повлияет на общий облик системы производства. Век энергии сменяется веком информации. Автоматизация производственных процессов, внедрение в народное хозяйство вычислительных машин приводят к еще более быстрому, чем прежде, росту производительности труда и придают системе производства характер автономной самоуправляющейся системы.
Простой рефлекс (раздражимость)
Простейший вариант нервной сети — это вообще ее отсутствие. В этом случае рецепторы непосредственно связаны с эффекторами и возбуждение с одного или нескольких рецепторов передается на один или несколько эффекторов. Такую прямую связь между возбуждением рецептора и эффектора мы назовем простым рефлексом.
Этот этап — третий по нашей сквозной нумерации этапов эволюции — является пограничным между химической и кибернетической эрами. Тип кишечнополостных представляет животных, застывших на уровне простого рефлекса. Возьмем, например, гидру, которую изучают в школе как типичного представителя кишечнополостных. Тело гидры (рис. 1.8) имеет вид удлиненного мешочка. Его внутренность — кишечная полость — сообщается с внешней средой через ротовое отверстие, окруженное несколькими щупальцами. Стенки мешочка состоят из двух слоев клеток: внутреннего (энтодерма) и внешнего (эктодерма). И в эктодерме, и в энтодерме много мышечных клеток, содержащих волоконца, которые могут сокращаться, приводя тело гидры в движение. Кроме того, в эктодерме есть и нервные клетки, причем клетки, расположенные ближе всего к поверхности, — это рецепторы, а клетки, заложенные глубже, среди мышц, — эффекторы. Если к гидре прикоснуться иглой, она сжимается в комочек. Это простой рефлекс, вызванный передачей возбуждения от рецепторов к эффекторам.
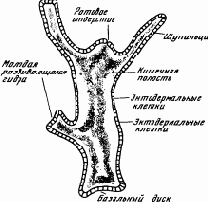
Рис. 1.8. Строение гидры
Но гидра способна и к гораздо более сложному поведению. Захватив добычу, она подтягивает ее щупальцами к ротовому отверстию и заглатывает. Такое поведение тоже можно объяснить совокупным действием простых рефлексов, связывающих эффекторы и рецепторы локально — в пределах большого участка тела. Например, следующая модель щупальца объясняет его способность обвиваться вокруг падающих предметов (рис. 1.9). Представим себе некоторое количество звеньев, соединенных между собой шарнирами (для простоты рассматриваем плоскую картину). Точки A и B, A' и B', B и C, В' и C' и т. д. соединены между собой тяжами, которые могут сокращаться (мышцы). Все эти точки являются чувствительными, возбуждаясь от прикосновения к предмету (рецепторы). Возбуждение каждой точки приводит к сокращению двух соседних с нею тяжей (рефлекс).
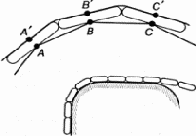
Рис. 1.9. Модель щупальца
Путь к открытию
Ферма был только математиком. Декарт был прежде всего философом. Его размышления выходили далеко за пределы математики и имели дело с проблемами сущности бытия и познания. Декарт — основоположник философии рационализма, утверждающей неограниченную способность человека познавать мир, исходя из некоторого числа интуитивно ясных истин и продвигаясь, шаг за шагом вперед с помощью определенных правил или методов. Эти два слова — ключевые для всей философии Декарта. «Правила для руководства ума» — так называется его первое философское сочинение, «Рассуждение о методе» — второе. «Рассуждение о методе» было издано в 1637 г. в одном переплете с тремя физико-математическими трактатами: «Диоптрика», «Метеоры» и «Геометрия» и предшествовало им как изложение философских принципов, лежащих в основе следующих частей. Декарт выдвигает в этом сочинении следующие четыре принципа исследования:
Не признавать истинным ничего, кроме того, что с очевидностью познается мною таковым, т. е. тщательно избегать поспешности и предубеждений и принимать в свои суждения только то, что представляется моему уму так ясно и отчетливо, что ни в коем случае не возбуждает во мне сомнения. Разделять каждое из рассматриваемых мною затруднений на столько частей, на сколько возможно и сколько требуется для лучшего их разрешения. Мыслить по порядку, начиная с предметов наиболее простых и легко познаваемых, и восходить мало-помалу, как по ступеням, до познания наиболее сложных, допуская существование порядка даже среди тех, которые не следуют естественно друг за другом. Составлять повсюду настолько полные перечни и такие общие обзоры, чтобы быть уверенным, что ничего не пропущено.Руководствуясь этими принципами, Декарт и приходит к своим математическим идеям. Вот как он сам описывает этот путь в «Рассуждении о методе»:
Мне не стоило большого труда отыскание того, с чего следует начинать, так как я уже знал, что начинать надо с самого простого и доступного пониманию; учитывая, что среди всех, кто ранее исследовал истину в науках, только математики смогли найти некоторые доказательства, т.
е. представить доводы несомненные и очевидные, я уже не сомневался, что начинать надо именно с тех, которые исследовали они... Но я не имел намерения изучать на этом основании все отдельные науки, обычно именуемые математикой. Видя, что хотя их предметы различны, но все же они сходны между собой в том, что рассматривают не что иное, как различные встречающиеся в предметах отношения, я подумал, что мне следует лучше исследовать эти отношения вообще, мысля их не только в тех предметах, которые облегчали бы мне их познание, и никоим образом не связывая с этими предметами, чтобы тем лучше применить их потом ко всем другим, к которым они подойдут. Затем, приняв во внимание, что для изучения этих отношений мне придется рассматривать каждое из них в отдельности и лишь иногда запоминать или истолковывать их по несколько вместе, я подумал, что для лучшего рассмотрения их в отдельности я должен представить их себе в виде линий, потому что я не находил ничего более простого, что я мог бы представить себе более отчетливо в своем воображении и ощущении. Но для того, чтобы лучше удержать их в памяти или сосредоточить внимание сразу на нескольких, надо выразить их какими-то возможно более краткими знаками. Благодаря такому способу, я мог заимствовать все лучшее в геометрическом анализе и в алгебре и исправить все недостатки одного при помощи другой.
Из этого чрезвычайно интересного свидетельства видно, что Декарт отчетливо осознает семантическую новизну своего языка, основанного на абстрактном понятии отношения и применимого ко всем явлениям действительности. Линии служат лишь для иллюстрации понятия отношения подобно тому, как набор палочек служит для иллюстрации понятия числа. В математических работах то, что обозначается буквами, Декарт и последующие математики называют по традиции величинами, но по смыслу это не пространственные геометрические величины греков, а их отношения. Понятие величины у Декарта так же абстрактно, как понятие числа. Но оно, конечно, никак не сводится к понятию числа в точном смысле слова, т.
е. рационального числа. В «Геометрии», поясняя свои обозначения, Декарт указывает, что они подобны (а не тождественны) обозначениям арифметической алгебры.
Подобно тому, как вся арифметика состоит только из четырех–пяти действий, а именно: сложения, вычитания, умножения, деления и извлечения корня... так и в геометрии для нахождения искомых отрезков надо только прибавлять или отнимать другие отрезки; или, имея отрезок, который я для более наглядного сопоставления с числами буду называть единицей и который вообще можно выбирать произвольно и, имея, кроме него, два других отрезка, требуется найти четвертый, который так относится к одному из этих двух, как другой к единице, — это равносильно умножению; или же требуется найти четвертый отрезок, который так относится к одному из двух данных, как единица к другому, — это равносильно делению; или, наконец, требуется найти одно, два или несколько средних пропорциональных между единицей и другим отрезком — это равносильно извлечению корня — квадратного, кубического и т. д. И я нисколько не колеблюсь ввести эти арифметические термины в геометрию, чтобы сделать мое изложение более понятным.
Семантика алгебраического языка Декарта много сложнее семантики арифметического и геометрического языков, опирающихся на наглядные образцы. Использование такого языка изменяет взгляд на отношение между языком и действительностью. Обнаруживается, что буквы математического языка могут обозначать не только числа и фигуры, но и нечто гораздо более абстрактное (точнее, конструктное). Отсюда берет начало изобретение новых математических языков и диалектов, введение новых конструктов. Прецедент был создан Декартом. Фактически Декарт заложил основу описания явлений действительности с помощью формализованных символьных языков.
Непосредственное значение реформы Декарта заключалось в том, что она развязала руки математикам для создания в абстрактной символьной форме исчисления бесконечно малых, основные идеи которого в геометрической форме были известны еще древним.
Если к дате выхода в свет «Геометрии» мы прибавим полвека, то очутимся в эпохе Лейбница и Ньютона, а еще через полвека — в эпохе Эйлера.
История науки показывает, что наибольшая слава достается обычно не тем, кто закладывает основы и, конечно, не тем, кто занимается мелкими заключительными доделками, а тем, кто в новом направлении мысли первым получает крупные результаты, поражающие воображение современников или ближайших потомков. Такую роль в европейской физико-математической науке сыграл Ньютон. Между тем известно высказывание Ньютона:
Если я видел дальше, чем Декарт, то потому, что я стоял на плечах Гигантов3.
Это, конечно, свидетельствует о скромности гениального ученого, но является также признанием долга перед первопроходцами со стороны «первополучателей». Яблоко, прославившее Ньютона, выросло на дереве, которое посадил Декарт.
1
Т. е. со сторонами, равными неравным частям.
2 Пробуждающаяся наука. Гл. 8.
3 If I have seen farther than Descartes, it is by standing on shoulders of giants.
Расхождение траекторий
И все же человек чрезвычайно мал по сравнению не только с Вселенной, но и с человечеством в целом, что снова склоняет нас к мысли о незначительности личного волевого акта, и закон больших чисел, казалось бы, должен укрепить нас в этой мысли. Надо заметить, что поверхностно понятые и неправильно приложенные научные истины очень часто способствуют принятию ложных концепций. Так обстоит дело и в данном случае. Опираясь на закон больших чисел, рассуждают следующим образом. На Земле живет три миллиарда человек (вариант: в нашей стране двести пятьдесят миллионов). Судьба человечества есть результат их совместных действий. Поскольку вклад каждого человека в эту сумму равен одной трехмиллиардной, ни один человек не может надеяться существенно повлиять на ход истории — разве что случайно. Играют роль лишь общие факторы, влияющие на поведение многих людей одновременно.
В действительности это рассуждение содержит грубую ошибку, состоящую в том, что закон больших чисел применим лишь к совокупности независимых подсистем. К человечеству его можно было бы применить в том случае, если бы все три миллиарда людей действовали абсолютно независимо и вообще не знали бы ничего друг о друге. Но это далеко не так. Человечество — большая и сильно связанная система; поступки одних людей самым серьезным образом влияют на поступки других. Такие системы обладают, вообще говоря, свойством расхождения траекторий, т. е. небольшие вариации в начальном состоянии системы становятся со временем все больше и больше. Ситуации, в которых закон расхождения траекторий проявляется с несомненной очевидностью, мы называем кризисными. В кризисной ситуации огромные перемены в состоянии системы зависят от ничтожных (в масштабе системы) причин. В такой ситуации действия одного человека, быть может даже одно слово, сказанное им, могут иметь решающее значение. Кризисные ситуации мы склонны рассматривать как редкие, даже исключительные, но мы знаем множество постоянно действующих факторов, приводящих к многократному усилению влияния одного человека.
Это так называемые триггерные механизмы, т. е. механизмы со спусковым крючком. Требуется совершенно незначительное усилие, чтобы нажать на спусковой крючок или кнопку управления, а последствия, вызванные этим действием, могут быть огромны. Вряд ли есть необходимость говорить, как много таких механизмов в человеческом обществе.
И все же идея о маленьком человеке — этот фиговый листок, которым мы прикрываем на людях срам своей трусости, — не сдается без боя. Большинство людей, — говорит «маленький человек», — не участвуют в кризисных ситуациях и не имеют доступа к спусковым крючкам.
Наверное, многие помнят английский стишок, переведенный Маршаком, который заканчивается словами:
Враг вступает в город, пленных не щадя,
Потому что в кузнице не было гвоздя!
В стишке описан триггерный механизм, который от растяпы-кузнеца, у которого не было гвоздя, ведет к поражению армии. Мы относимся к этой истории с большой дозой юмора, не желая принимать ее совсем всерьез. Почему? Не потому ли, что таких многоступенчатых зависимостей не бывает? Отнюдь нет. Вся наша жизнь состоит из них. То же говорит математическое исследование больших связанных систем: траектории расходятся. Первоначально незначительное отклонение — отсутствие в кузнице гвоздя — шаг за шагом увеличивается: подкова пропала, лошадь захромала, командир убит, конница разбита, армия бежит. А скептически мы относимся к подобным длинным цепочкам потому, что в обыденной жизни нам почти никогда не удается с достоверностью проследить их от начала до конца. Во-первых, каждая связь между звеньями цепочки имеет вероятностный характер: захромавшая лошадь вовсе не обязательно губит командира. Во-вторых, прослеживание связи событий постоянно ставит вопросы типа: «А что было бы, если бы не...?» Трудно найти двух людей, дающих одинаковые ответы на серию таких вопросов, а вернуть время назад и посмотреть, невозможно. Наконец, в-третьих, мы практически никогда не обладаем необходимой информацией.
Но тот факт, что мы не можем проследить этих цепочек в обратном направлении, не должен затемнять нам сознание их существования, когда мы думаем о последствиях наших поступков.Кризисные ситуации редки не потому, что малые причины редко вызывают большие последствия — это происходит постоянно, но потому, что это превращение редко предстает перед нами со всей очевидностью. Мы никогда не можем в точности предвидеть результаты наших поступков. Единственное, что нам доступно, — это установить общие принципы, руководствуясь которыми мы увеличиваем вероятность Добра, т. е. вероятность тех последствий, которые считаем желательными. Мы должны действовать в соответствии с этими принципами, рассматривая каждую ситуацию как кризисную, ибо важность каждого акта нашей воли может оказаться огромной. Действуя так всегда, мы, несомненно, внесем свой положительный вклад в дело Добра — вот здесь закон больших чисел действует в полную силу.
Распознаватели и классификаторы
Нервную сеть, решающую задачу распознавания, мы назовем распознавателем, а состояние эффектора на его выходе будем называть просто состоянием распознавателя. Отправляясь от понятия распознавателя, мы введем несколько более общее понятие классификатора. Распознаватель делит множество всех мыслимых ситуаций на два непересекающихся подмножества: A и не A. Можно представить себе деление полного множества ситуаций на произвольное число n пересекающихся подмножеств. Такие подмножества называют обычно классами. Теперь вообразим некую подсистему C, имеющую n возможных состояний и связанную нервной сетью с рецепторами таким образом, что, когда ситуация принадлежит к i-му классу (i-му понятию), подсистема C приходит в i-е состояние. Такую подсистему вместе с нервной сетью мы будем называть классификатором по множеству n понятий (классов), а, говоря о состоянии классификатора, подразумевать состояние подсистемы C (выходной подсистемы). Распознаватель — это, очевидно, классификатор с числом состояний n = 2.
В системе, организованной по двоичному принципу подобно нервной системе, подсистема C с n состояниями будет, конечно, состоять из какого-то числа элементарных подсистем с двумя состояниями, которые можно рассматривать как выходные подсистемы (эффекторы) распознавателей. Состояние классификатора, следовательно, будет описываться указанием состояний ряда распознавателей. Однако эти распознаватели могут быть тесно связаны между собой как по структуре сети, так и по выполняемой функции в нервной системе, и в этом случае их следует рассматривать в совокупности как один классификатор.
Если не накладывать никаких ограничений на число состояний, то понятие «классификатор» фактически теряет смысл. Действительно, всякая нервная сеть сопоставляет каждому входному состоянию одно определенное выходное состояние; следовательно, каждому выходному состоянию соответствует множество входных состояний, и эти множества не пересекаются. Таким образом, всякое кибернетическое устройство с входом и выходом можно формально рассматривать как классификатор. Придавая этому понятию более узкий смысл, мы будем считать, что число выходных состояний классификатора гораздо меньше, чем число входных состояний, так что классификатор действительно «классифицирует» входные состояния (ситуации) по относительно небольшому числу больших классов.
Рефлекс как функциональное понятие
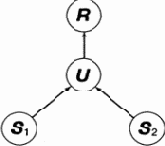
Понятия рефлекса и ассоциации — не структурные, а функциональные понятия. Связь между стимулом S и реакцией R в рефлексе (рис. 3.2) — не передача информации от одной подсистемы к другой, а переход из одного обобщенного состояния в другое. Это разграничение необходимо, чтобы не смешивать рефлекс как определенную функциональную схему, описывающую поведение, с воплощением этой схемы, т. е. с кибернетическим устройством, обнаруживающим эту схему поведения.
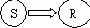
Рис. 3.2. Функциональная схема безусловного рефлекса
Путаница легко может возникнуть, ибо простейшее воплощение рефлекторного поведения имеет структурную схему, совпадающую по внешности со схемой на рис. 3.2, только под S и R надо в ней понимать материальные подсистемы, фиксирующие стимул и реакцию. Такое совпадение не совсем случайно. Как мы уже говорили при определении функциональной схемы, разбиение множества всех состояний системы на подмножества, приписываемые вершинам графа, тесно связано с разбиением системы на подсистемы. В частности, с каждой подсистемой, которая может находиться в двух состояниях («да» и «нет»), можно связать множество всех состояний системы в целом, при которых эта система находится в определенном состоянии, скажем «да». Проще говоря, при определении обобщенного состояния мы учитываем только состояние данной подсистемы, а что делается с остальными подсистемами, нам безразлично. Допустим, что буквы S и R обозначают именно такие подсистемы, т. е. подсистема S есть распознаватель стимула (множества ситуаций) S, а подсистема R - эффектор, вызывающий реакцию R. Тогда утверждение, что «да» в подсистеме S передается по каналу связи (стрелка) в подсистему R, приводя ее также в состояние «да», совпадает с утверждением, что обобщенное состояние S переходит (стрелка) в состояние R. Поэтому структурная и функциональная схемы оказываются очень похожими. Правда, на структурной схеме никак не отражено, что «да» вызывает «да», а не «нет», в то время как в этом вся суть рефлекса. Рефлекс, как уже говорилось, понятие функциональное.
Решение уравнений
С развитием техники счета и вообще с развитием цивилизации стали появляться и решаться все более сложные уравнения. Древние не знали, конечно, современного алгебраического языка, они выражали уравнения на обычном разговорном языке подобно тому, как это делается в наших школьных учебниках арифметики. Но это не меняет сущности задач, которые они решали (и так называемых арифметических школьных задач), как задач на решение уравнений.
Величину, подлежащую определению, египтяне называли «аха», что переводят как «некоторое количество» или «куча». Вот пример формулировки задачи из египетского папируса: «количество и его четвертая часть дают вместе 15». Это задача «на части» по современной арифметической терминологии, а на алгебраическом языке она соответствует уравнению
x + 1/4 x = 15.
Приведем пример более сложной задачи египетских времен.
Квадрат и другой квадрат, сторона которого есть 1/2 + 1/4 стороны первого квадрата, имеют вместе площадь 100. Вычисли мне это.
Решение в современных обозначениях:
x2 + (3/4 x)2 = 100, (1 + 9/16) x2 = 100,
5/4 x = 10, x = 8, 3/4 x = 6,
Описание решения в папирусе:
Возьми квадрат со стороной 1 и возьми 1/2 + 1/4 от 1, т. е. 1/2 + 1/4 в качестве стороны второй площади. Помножь 1/2 + 1/4 на самое себя, это дает 1/2 + 1/16. Поскольку сторона первой площади взята за 1, а второй за 1/2 + 1/4, то сложи обе площади вместе; это дает 1 + 1/2 + 1/16. Возьми корень отсюда: это будет 1 + 1/4. Возьми корень из данных 100: это будет 10. Сколько раз входит 1 + 1/4 в 10? Это входит 8 раз.
Дальше текст не сохранился, но конец очевиден: 8 × 1 = 8 — сторона первого квадрата, 8 × (1/2 + 1/4) = 6 — второго.
Египтяне умели решать только линейные и простейшие квадратные уравнения с одним неизвестным. Вавилоняне продвинулись гораздо дальше. Вот пример задачи из вавилонских текстов.
Площади двух моих квадратов я сложил: 25 25/60. Сторона второго квадрата равна 2/3 стороны первого и еще 5.
Далее следует совершенно правильное ее решение. Эта задача эквивалентна системе уравнений с двумя неизвестными:
x2 + y2 = 25 25/60, y = 2/3 x + 5.
Вавилоняне умели решать полное квадратное уравнение
x2 ± ax = b,
кубические уравнения
x3 = a и x2 (x + 1) = a,
системы уравнений, подобные приведенной выше, а также вида
x2 ± y = a, xy = b.
Кроме того, они пользовались формулами
(a + b)2 = a + 2ab + b2 и (a + b)(a - b) = a2 - b2,
умели суммировать арифметические прогрессии, знали суммы некоторых числовых рядов и числа, которые впоследствии подучили название пифагоровых (такие целые числа x, y, z, что х2 + у2 = z2).
Роль общих принципов
Бэкон выдвинул программу постепенного введения теоретических положений («причин и аксиом») все большей и большей общности, начиная с эмпирических единичных данных. Этот процесс он назвал индукцией (т. е. введением) в отличие от дедукции (выведения) теоретических положений меньшей общности из положений большей общности (принципов). Бэкон был большим противником общих принципов, он говорил, что разум нуждается не в крыльях, которые поднимали бы его ввысь, а в свинце, который притягивал бы его к земле. В период «первоначального накопления» опытных фактов и простейших эмпирических закономерностей, а также в качестве противовеса средневековой схоластике эта концепция еще имела некоторое оправдание, но в дальнейшем оказалось, что крылья разуму все-таки нужнее свинца. Во всяком случае, так обстоит дело в теоретической физике. В подтверждение предоставим слово такому несомненному авторитету в этой области, как Альберт Эйнштейн. В статье «Принципы теоретической физики»3 он пишет:
Для применения своего метода теоретик в качестве фундамента нуждается в некоторых общих предположениях, так называемых принципах, исходя из которых он может вывести следствия. Его деятельность, таким образом, разбивается на два этапа. Во-первых, ему необходимо отыскать принципы, во-вторых, развивать вытекающие из этих принципов следствия. Для выполнения второй задачи он основательно вооружен еще со школы. Следовательно, если для некоторой области, т. е. совокупности взаимозависимостей, первая задача решена, то следствия не заставят себя ждать. Совершенно иного рода первая из названных задач, т. е. установление принципов, могущих служить основой для дедукции. Здесь не существует метода, который можно было бы выучить и систематически применять для достижения цели. Исследователь должен, скорее, выведать у природы четко формулируемые общие принципы, отражающие определенные общие черты множества экспериментально установленных фактов.
В другой статье («Физика и реальность») Эйнштейн высказывается весьма категорически:
Физика представляет собой развивающуюся логическую систему мышления, основы которой можно получить не выделением их какими-либо индуктивными методами из пережитых опытов, а лишь свободным вымыслом.
Слова о «свободном вымысле» означают, конечно, не то, что общие принципы совершенно не зависят от опыта, а то, что они не определяются опытом однозначно. Пример, который Эйнштейн часто приводит, таков. Небесная механика Ньютона и общая теория относительности Эйнштейна построены на одних и тех же опытных фактах. Однако они исходят из совершенно различных, в некотором смысле даже диаметрально противоположных общих принципов, что проявляется и в различном математическом аппарате.
Пока «этажность» здания теоретической физики была невелика, и следствия из общих принципов выводились легко и однозначно, люди не осознавали, что при установлении принципов они имеют определенную свободу. В методе проб и ошибок расстояние между пробой и ошибкой (или успехом) было так невелико, что они не замечали, что пользуются методом проб и ошибок, а полагали, что непосредственно выводят (хотя это и называлось не дедукцией, а индукцией) принципы из опыта. Эйнштейн пишет:
Ньютон, творец первой обширной плодотворной системы теоретической физики, еще думал, что основные понятия и принципы его теории вытекают из опыта. Очевидно, именно в таком смысле нужно понимать его изречение «hypotheses non fingo» (гипотез не сочиняю).
Но со временем теоретическая физика превратилась в многоэтажную конструкцию, и вывод следствий из общих принципов стал делом сложным и не всегда однозначным, ибо часто оказывалось необходимым делать в процессе дедукции дополнительные предположения, чаще всего «непринципиальные» упрощения, без которых невозможно было бы довести расчет до числа. Тогда стало ясно, что между общими принципами теории и фактами, допускающими непосредственную проверку на опыте, существует глубокое различие: первые суть свободные конструкции человеческого разума, вторые — исходный материал, который разум получает от природы.
Правда, переоценивать глубину этого различия все- таки не следует. Если отвлечься от человеческих дел и стремлений, то окажется, что различие между теориями и фактами исчезает, — и те и другие являются некоторыми отражениями или моделями действительности вне человека. Различие заключается в уровне, на котором происходит овеществление модели. Факты, если они полностью «деидеологизированы», определяются воздействием внешнего мира на нервную систему человека, которую мы вынуждены рассматривать (пока) как не допускающую переделки, поэтому мы и относимся к фактам как к первичной реальности. Теории — это модели, овеществленные в языковых объектах, которые целиком в нашей власти, поэтому мы можем отбросить одну теорию и заменить ее другой с такой же легкостью, как заменяем устаревший инструмент на более совершенный.
Возрастание абстрактности (конструктности) общих принципов физических теорий, их отдаление от непосредственных опытных фактов приводит к тому, что в методе проб и ошибок все труднее становится найти пробу, имеющую шансы на успех. Разум начинает просто нуждаться в крыльях для воспарения, о чем и говорит Эйнштейн. С другой стороны, увеличение дистанции от общих принципов до проверяемых следствий делает общие принципы в известных пределах неуязвимыми для опыта, на что также часто указывали классики новейшей физики. Обнаружив расхождение между следствиями теории и экспериментом, исследователь оказывается перед альтернативой: искать причины расхождения в общих принципах теории или же где-то на пути от принципов к конкретным следствиям. Вследствие дороговизны общих принципов и больших затрат, необходимых для перестройки теории в целом, сначала всегда пробуют второй путь. Если удается достаточно изящным способом модифицировать вывод следствий из общих принципов так, что они согласуются с экспериментом, то все успокаиваются и проблема считается решенной. Но иногда модификация выглядит явно, как грубая заплата, а порой заплаты наслаиваются друг на друга и теория начинает трещать по всем швам; тем не менее, ее выводы согласуются с данными опыта и она продолжает сохранять свою предсказательную силу.Тогда возникают вопросы: как следует относиться к общим принципам такой теории? Надо ли стремиться заменить их какими-то другими принципами? При какой степени «залатанности» имеет смысл отбрасывать старую теорию?
Рост науки
Наука растет и растет стремительно — по экспоненциальному закону, т. е. таким образом, что за каждые сколько-то лет ее количественные характеристики возрастают во столько-то раз. Общее число статей в научных журналах всего мира удваивается за 12–15 лет1. Число научных работников удваивается: в Западной Европе — за 15 лет, в США — за 10 лет, в СССР — за 7 лет. При таком бешеном темпе роста современное поколение ученых составляет 9/10 суммарной численности всех ученых, когда-либо живших на Земле.
Вместе с наукой экспоненциально растут и другие количественные характеристики, относящиеся к человечеству: общая численность людей и общий объем производства материальных ценностей. Но по темпам роста наука значительно обгоняет их. Темпы роста населения, производства и науки находятся, грубо говоря, в пропорции 1:2:4. Это — здоровая пропорция, отражающая такую эволюцию организма, когда масса мышц возрастает быстрее, чем общая масса тела, а масса мозга возрастает быстрее, чем масса мышц. Правда, с территориальным распределением прироста дело обстоит неблагополучно: высокий прирост населения приходится в основном на страны с низким приростом производства и практически нулевым вкладом в мировую науку. Однако с этой болезнью роста человечество, будем надеяться, сумеет справиться. В том, что это болезнь роста, вряд ли можно усомниться: ведь и быстрый рост населения в слаборазвитых странах обязан высокому уровню мировой науки (медицинское обслуживание, социальные сдвиги). Человечество уже сейчас представляет собой весьма интегрированную систему, и его общий взлет, передаваемый пропорцией 1:2:4, — результат развития науки — явление совсем недавнее. Если экстраполировать в прошлое современный прирост населения (порядка 2% в год), то окажется, что всего около тысячи лет назад на Земле должно было жить два человека!
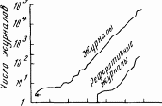
1700 1800 1900 2000
Рис. 14.1. Рост обшей массы научных журналов
Доля людей, занятых непосредственно в сфере науки, пока еще невелика даже в высокоразвитых странах — от 0,5 до 1%.
Сейчас она быстро растет, однако рано или поздно рост ее, очевидно, замедлится, она выйдет на постоянный уровень, величину которого трудно предсказать. Насколько можно судить по литературе, считается маловероятным, чтобы этот уровень превысил 25%. Ведь и мозг человека составляет по весу небольшую долю всего тела.
Абсолютное число людей, занимающихся научной деятельностью, будет, тем не менее, непрерывно возрастать, а вместе с ним будет непрерывно возрастать и количество производимой ими информации. Уже сейчас это количество огромно. Первые научные периодические издания начали выходить во второй половине XVII в. К началу 60-х годов нашего века их суммарное число составило 50 тыс. (рис. 14.1), продолжало выходить из них 30 тыс. изданий. Всего в них было опубликовано 6 млн. статей, и эта цифра увеличивалась на полмиллиона в год2. Общее число зарегистрированных патентов и авторских свидетельств превысило 13 млн.
Этот поток информации, требующий анализа, порождает серьезные трудности. Научная работа уже давно требует крайней степени специализации, однако, в последнее время все чаше возникает такое положение, когда ученый лишается возможности уследить за всеми новыми работами даже в своей узкой области. Перед ним встает дилемма: либо читать статьи, либо работать. Вдобавок вследствие технических трудностей распространения и переработки огромных количеств информации (можно это также назвать несовершенством системы информации в науке и технике) часто приходится затрачивать большие усилия на поиски нужной информации, и они не всегда приводят к успеху. В результате многие работы делаются повторно или не так, как их следовало бы делать. По оценке американских ученых от 10 до 20% научно-исследовательских и проектно-конструкторских работ можно было бы не проводить, если бы имелась информация об уже выполненных работах. Убытки от этого в США составили 1,25 млрд. долларов. Согласно Г.Н.Доброву, в 1946 г. 40% заявок на изобретения в области угольного комбайностроения отвергались как повторные.В 1961 г. эта цифра возросла до 85%.
Самопознание
У животных нет понятия о себе самом, это понятие не нужно для обработки информации, поступающей извне. Мозг животного можно сравнить с зеркалом, которое отражает окружающую действительность, но само ни в чем не отражается. В самом примитивном человеческом обществе каждому человеку присваивается имя, и каждый человек произносит свое имя и предложения, в которых его имя содержится. Таким образом, он сам — в виде предложений, содержащих его имя, — становится предметом своего внимания и изучения. Язык представляет собой как бы второе зеркало, в котором отражается весь мир, и в том числе каждый индивидуум, и в котором каждый индивидуум может увидеть (вернее, не может не увидеть!) самого себя. Так возникает понятие «Я». Если заключительный этап кибернетического периода можно назвать этапом познания, то эра разума — это эра самопознания. Система двух зеркал — мозга и языка создает возможность бесчисленного множества взаимных отражений без необходимости выходить из пространства между зеркалами. Это порождает неразрешимые загадки самопознания и в первую очередь загадку смерти.
Счет и измерение
Факты убедительно свидетельствуют о том, что счет возникает раньше, чем названия чисел. Иначе говоря, первоначально языковыми объектами для построения модели служат не слова, а выделенные однотипные предметы: пальцы, камешки, узелки, черточки. Это и естественно. При возникновении языка слова связываются только с теми понятиями, которые уже существуют, т. е. распознаются. Слова «один», «два» и, возможно, «три» появляются независимо от счета (если понимать под счетом процедуру, протяженную во времени и осознаваемую как таковая), ибо они опираются на соответствующие нейронные понятия. Словам для больших чисел взяться неоткуда. Чтобы передать численность какой-то группы предметов, человек пользуется стандартными предметами, устанавливая между ними — один за другим — взаимно однозначное соответствие. Это и есть счет. Когда счет становится распространенным и привычным делом, для наиболее часто встречающихся (т. е. небольших) групп стандартных предметов возникают и словесные обозначения. На некоторых числительных остались следы их происхождения. Так, русское слово «пять» подозрительно похоже на старославянское «пядь» — рука (пять пальцев).
Есть первобытные народы, у которых всего два или три числительных: один, два, три. Все остальное — много. Но это вовсе не исключает умения считать с помощью стандартных предметов и передавать о численности путем разбиения на двойки и тройки или путем таких, не редуцированных еще выражений, как «столько, сколько пальцев на двух руках, одной ноге и еще один». Просто потребность в счете еще не так велика, чтобы заводить специальные слова. Последовательность «один, два, три, много» отражает не неспособность к счету до четырех и дальше, как иногда думают, а различие, которое проводит человеческий мозг между первыми тремя числами и всеми остальными. Ибо совсем без напряжения и бессознательно мы распознаем только числа до трех. Для распознавания четверки надо уже специально сосредоточиться. Так что не только для дикарей, но и для нас все, что больше трех, много.
Чтобы передать большие числа, люди стали считать «большими единицами» — пятерками, десятками, двадцатками.
Во всех известных нам системах счета большие единицы кратны пяти, что свидетельствует о том, что первым счетным инструментом всегда становились пальцы. Из комбинации больших единиц возникли еще большие единицы. В древнеегипетских папирусах встречаются отдельные иероглифы, изображающие числа до десяти миллионов.
Начало измерения, как и счета, относится к глубокой древности: мы находим его уже у первобытных народов. Измерение предполагает умение считать и требует дополнительно введения единицы измерения — меры измерительной процедуры, состоящей в сравнении измеряемого с единицей. Древнейшие меры связаны с человеческим телом: шаг, локоть, фут (ступня).
С возникновением цивилизации потребность в счете и в умении выполнять арифметические действия резко увеличивается. При развитом общественном производстве регулирование отношений между людьми: обмен, раздел имущества, налогообложение — требует знания арифметики и элементов геометрии. И мы находим эти знания в древнейших из известных нам цивилизаций — вавилонской и египетской.
Синтаксис и семантика
В заключение нашего краткого очерка логики рассмотрим вопрос о связи языка логики и естественного языка. Попутно будут введены важные понятия синтаксис и семантика языка.
Вспомним фразу о рыжем псе, которую мы разложили в набор высказываний, выражаемых с помощью предикатов. Смысл, значение, этого набора совпадает со смыслом исходной фразы, а форма записи, структура текста, существенно отличается. В семиотике (наука, изучающая знаковые системы) совокупность правил построения элементов языка называют его синтаксисом, а связь между элементами языка и их значениями — семантикой. Следовательно, первое, что бросается в глаза при сравнении логического и естественного языков, это то, что язык логики имеет другой синтаксис. Этот синтаксис прост и единообразен. Он основан на стиле обозначений, сложившемся в математике, — конструирование более сложных элементов языка из более простых, изображается по аналогии с математической записью операций и функций. Синтаксис языка логики полностью формализован, т. е. существует набор четко сформулированных правил, с помощью которых можно построить любой языковый элемент. Далее, какой бы правильно построенный элемент языка (объект или высказывание) мы ни взяли, всегда можно восстановить путь, которым этот элемент был построен, его структуру. Этот процесс называется синтаксическим анализом элемента. Легко убедиться, что в языке логики синтаксический анализ чрезвычайно прост и однозначен.
Синтаксис (в смысле семиотики) естественного языка — это его грамматика, т. е. правила конструирования предложений из слов (синтаксис в узком, лингвистическом смысле слова) и правила конструирования слов из букв (морфология). В отличие от языка логики синтаксис естественного языка отнюдь не является полностью формализованным. Он включает в себя множество правил с великим множеством исключений. Это различие вполне понятно: язык логики создавался искусственно, а естественный язык — продукт долгого развития, которым никто не управлял сознательно, никто не пользовался заранее продуманным планом.
Грамматика естественного языка — это не конструирование, а исследование уже готовой системы, попытка вскрыть и по возможности сформулировать те правила, которыми говорящие на этом языке люди пользуются неосознанно.
Синтаксический анализ предложений естественного языка нередко требует обращения к семантике, ибо без учета смысла, значения предложения, он оказывается неоднозначным. Возьмем, например, такую фразу: «Вот списки студентов, которые сдали зачет по физике». Здесь определение «которые сдали зачет по физике» относится к студентам. Если для уточнения синтаксической структуры фразы использовать скобки подобно тому, как это делается при записи алгебраических или логических выражений, то скобки надо поставить так: «Вот списки (студентов, которые... и т. д.)». Теперь возьмем такое предложение: «Вот списки студентов, которые лежали в шкафу у декана». Формально структура этой фразы в точности такая же, как и предыдущей. На самом же деле здесь подразумевается другая расстановка скобок, а именно «Вот (списки студентов), которые... и т. д.». Мысленно расставляя скобки таким образом, мы опираемся исключительно на смысл фразы, ибо не допускаем, что студенты могли лежать в шкафу у декана.
Вообще оборот со словом «который» — весьма коварная вещь. Л.Успенский в книге «Слово о словах» рассказывает, что однажды он увидел такое объявление:
«Граждане, сдавайте утиль дворнику, который накопился!»
Неудивительно, что этот оборот не прижился в математической логике!
Системный аспект культуры
Продолжим наше шествие по этапам эволюции. Из области биологии мы перешли в область истории человечества. В главе 5 был дан набросок истории «материальной» культуры. Теперь предметом нашего анализа будет история развития языка и мышления — важнейшей составной части «духовной» культуры. Как мы уже отмечали, деление культуры на «материальную» и «духовную» весьма условно и, когда мы хотим подчеркнуть это, мы помещаем их в кавычки. Использование орудия и тем более создание нового орудия требуют работы воображения и сопровождаются эмоциями, что дает основания рассматривать эти явления как часть «духовной» культуры. В то же время процесс мышления проявляется как определенная языковая деятельность, направленная на вполне материальные предметы — языковые объекты. Язык и мышление, с одной стороны, и материальная культура, с другой стороны, связаны друг с другом теснейшим образом. Историк, поставивший себе задачу детально исследовать механизм развития культуры, не может рассматривать эти явления иначе, как в их взаимосвязи. Он должен также учесть другие стороны культуры и в первую очередь социальную структуру общества, а также влияние природных условий, исторических случайностей и прочих факторов. Но данное исследование не является историческим и наша задача проще: не вдаваясь в детали исторического развития, описать то, что произошло, с кибернетической, или, как еще говорят, с системной, точки зрения. Как и в вопросе о происхождении человека, нас не будут интересовать хитросплетения исторических обстоятельств, приведших к тому, что тот или иной шаг в развитии культуры был сделан в том или ином месте и в то или иное время. Подход наш остается весьма глобальным и общим. Нас интересует лишь один (но зато самый важный в механизме развития!) аспект культуры — ее структура как иерархии по управлению. Соответственно и развитие культуры мы будем рассматривать как усложнение этой иерархии путем последовательных метасистемных переходов. Мы покажем, что, как и в случае биологического развития, важнейшие этапы развития языка и мышления отделяются друг от друга именно метасистемными переходами.
Сложный рефлекс
Простая рефлекторная связь между возбудимой и мышечной клетками естественно возникает в процессе эволюции по методу проб и ошибок: если оказывается, что корреляция между возбуждением одной клетки и сокращением другой полезна для животного, то эта корреляция устанавливается и закрепляется. При механическом копировании связанных клеток в процессе роста и размножения природа получает систему параллельно действующих простых рефлексов, подобную щупальцу гидры. Но когда в ее (природы) распоряжении оказывается множество рецепторов и эффекторов, связанных попарно или локально, у нее «возникает искушение» усложнить систему связей путем введения промежуточных нейронов. Выгодность этого следует из того, что при наличии системы связей между всеми нейронами становятся возможными такие формы поведения, которые невозможны при ограничении парными или локальными связями. Последнее утверждение можно доказать простым подсчетом всевозможных способов преобразования ситуации в действие при том и другом способах связи. Пусть, например, у нас есть n попарно связанных рецепторов и эффекторов. Связь в каждой паре может быть либо положительная (возбуждение вызывает возбуждение, покой — покой), либо отрицательная (возбуждение вызывает покой, покой — возбуждение). Следовательно, всего возможно 2n вариантов связи, т. е. 2n вариантов поведения. Если же предположить, что система связей может быть произвольная, т. е. состояние возбуждения или покоя каждого эффектора может произвольным образом зависеть от состояния всех рецепторов, то подсчет всевозможных вариантов поведения приводит к числу 2(2n)n, неизмеримо большему, чем 2n. Совершенно такой же расчет приводит к заключению, что объединение любых подсистем, связывающих независимо друг от друга группы рецепторов и эффекторов в единую систему, всегда приводит к огромному возрастанию числа возможных вариантов поведения. Поэтому на протяжении всей истории жизни эволюция нервной системы проходит под знаком увеличения централизации.
Однако централизация централизации рознь.
Если связать все нейроны в один бессмысленно запутанный клубок, то, несмотря на крайнюю «централизованность» такой системы, она вряд ли будет иметь шансы выжить в борьбе за существование. Централизация ставит следующую проблему: как из всех мыслимых способов соединения многих рецепторов с многими эффекторами (с помощью промежуточных нейронов, если потребуется) выбрать такой способ, который будет каждой ситуации сопоставлять правильное, т. е. полезное для выживания и размножения, действие? Ведь подавляющее большинство способов соединения не обладает этим свойством.
Мы знаем, что каждый новый шаг на пути усложнения живых структур природа делает по методу проб и ошибок. Посмотрим, что дает непосредственное применение метода проб и ошибок к нашей проблеме. Рассмотрим для примера небольшую систему из ста рецепторов и ста эффекторов. Допустим, что в нашем распоряжении сколько угодно нейронов для создания промежуточной нервной сети и что мы умеем легко определять, дает ли данный способ соединения нейронов правильную реакцию на каждую ситуацию. Будем перебирать все мыслимые способы, пока не натолкнемся на нужный. При n = 100 число функционально различных нервных сетей между n
рецепторами и n эффекторами есть
2(2n)n
? 10(1032).
Число это невообразимо велико. Перебор такого числа вариантов недоступен не только нам, но и нашей матушке-природе. Если бы каждый атом во всей видимой нами части Вселенной занимался просмотром вариантов и перебирал бы их со скоростью миллиард штук в секунду, то и за миллиард миллиардов лет (а наша Земля существует не более десяти миллиардов лет) не была бы просмотрена и миллиардная доля общего числа вариантов.
Между тем как-то ведь происходит формирование эффективно работающей нервной сети! Причем число рецепторов и эффекторов у высших животных исчисляется не сотнями и не тысячами, а миллионами.
Разгадка кроется в иерархическом строении нервной системы.
Здесь нам снова необходим экскурс в область общекибернетических понятий. Четвертый этап эволюции мы назовем этапом сложного рефлекса, но дать определение этому понятию сможем лишь после того, как познакомимся с некоторыми фактами об иерархически устроенных нервных сетях.
1
Мы следуем в основном докладу С.Э.Шноля «Сущность жизни. Инвариантность общего направления биологической эволюции» (Диалектика и современное естествознание: Матер. семинара. Дубна, 1967)
Смешное и прекрасное
Но качественные отличия все-таки интереснее. Мы уже установили, что наличие специального аппарата управления ассоциированием делает для человека обучение активным процессом, связанным с положительными и отрицательными эмоциями. Это истинно человеческие эмоции, недоступные существам, которые не обладают указанным аппаратом. Из того факта, что целью ассоциирования является построение модели (или моделей) внешней среды, можно сделать вывод, что новая эмоция будет иметь положительный знак в случае установления ассоциации, улучшающей мозговую деятельность мира. Эту эмоцию можно назвать удовольствием от новизны, употребляя термин «новизна» в том смысле, который мы придаем ему выше. Соответствующую отрицательную эмоцию называют скукой. Выше мы перечисляли критерии установления и закрепления ассоциаций и отделяли критерий новизны от критерия наличия эмоционального подкрепления. Мы имели в виду обычные эмоции, общие для человека и животного. Возведя удовольствие от новизны в ранг эмоции, мы можем объявить третий критерий частным случаем первого. Тогда мы можем сказать, что непроизвольное ассоциирование всегда связано с эмоциональным подкреплением, но человек по сравнению с животным обладает принципиально новым классом эмоций.
Да, именно классом. «Удовольствие от новизны» — очень общий термин, покрывающий не одну эмоцию, а целый класс их. Можно сразу указать два явно отличающихся представителя этого класса: чувство смешного и чувство прекрасного. Вряд ли кто-нибудь в настоящее время возьмется утверждать, что он до конца понимает природу этих эмоций и может дать им сколько-нибудь детальную кибернетическую интерпретацию. Однако несомненно, что они неотделимы от познания мира, от создания новых моделей.
Что вызывает у нас смех? Совершенно неожиданное, но в то же время законное и задним числом вполне понятное нарушение «нормального» хода событий. Неожиданная ассоциация, бессмысленная на первый взгляд, но отражающая какие-то глубинные связи между вещами. Все это, конечно, создает новую модель мира и доставляет удовольствие, пропорциональное ее новизне.
Конец новизны — это конец смешного. Когда нас пытаются смешить в соответствии с хорошо знакомой моделью, мы называем такой юмор плоским. Но это понятие чрезвычайно относительно. Кому незнакома ситуация, когда в ответ на рассказанный анекдот один слушатель разражается хохотом, а другой лишь кисло усмехается? Их различает, очевидно, отсутствие или наличие соответствующей модели. Очень важна для уяснения природы юмора и другая ситуация: когда один хохочет, а другой непонимающе хлопает глазами. «Не дошло!» — говорят в таких случаях. Шутка оказалась слишком тонкой для этого человека, она опирается на такие ассоциации, которых у него нет. Смешное всегда лежит на грани между тривиальным и непонятным. Эта грань у каждого своя, и она передвигается в процессе индивидуального развития. Ничто так отчетливо не проявляет культурного уровня человека, как его понимание смешного.
В чувстве прекрасного больше индивидуальных различий между людьми, оно тоньше и загадочнее, чем чувство смешного. Но в нем есть тот же динамизм, связанный с новизной впечатления. Частое повторение понравившегося музыкального произведения не только делает к нему равнодушным, но, в конце концов, внушает к нему отвращение. Острое ощущение прекрасного кратковременно, оно включает элемент откровения, восторженного удивления. Его можно описать также как внезапное усмотрение какого-то глубокого порядка, соответствия, смысла. Если пытаться дать кибернетическую интерпретацию этому явлению, можно предположить, что чувство прекрасного вызывают те впечатления, которые дают пищу для самых сложных и тонких моделей, реализующихся с помощью классификаторов высшего уровня. Эти классификаторы должны, очевидно, в максимальной степени сжимать информацию, распознавать чрезвычайно сложные понятия. А это и есть усмотрение глубокого внутреннего порядка в кажущемся беспорядке.
Все модели иерархичны. Более сложное строится из более простого, высшее опирается на низшее. Человек может быть недостаточно развит эстетически и не видеть красоты там, где ее видят другие.
Неподготовленному слушателю шедевр симфонической музыки покажется бессмысленным нагромождением звуков. С другой стороны, банальная мелодия или примитивный геометрический орнамент не вызовут у нас ощущения прекрасного: здесь порядок слишком очевиден. «У нас» — это у современного цивилизованного человека. Возможно, неандерталец, увидев серию точно вычерченных концентрических окружностей, был бы потрясен до глубины души. Прекрасное тоже всегда на грани между тривиальным и непонятным. Передвижение этой грани — эстетическое воспитание — есть познание мира, построение в мозгу новых моделей.
Мы берем чувство прекрасного в его, если угодно, чистом виде. В действительности оно бывает связано с другими человеческими чувствами, образуя часто неразрывные комплексы и влияя поэтому на многие сферы и аспекты общественной жизни. Это значение эстетических переживаний, которое можно назвать прикладным, признано давно и безусловно. С чистой эстетикой дело обстоит хуже. На протяжении всей истории человечества время от времени раздавались призывы покончить с нею раз и навсегда, как с чем-то не только бесполезным, но и прямо вредным. (Вредность понималась по-разному. Одни объявляли красоту греховной, другие — отвлекающей от классовой борьбы.) И напротив, делались попытки вульгарно-материалистического толка объяснить и «оправдать» прекрасное, сведя его к полезному в самом житейском, бытовом смысле слова. Последнее выглядит так, как если бы кто-то стал расхваливать транзисторный приемник, уверяя, что им можно забивать гвозди и колоть орехи. Это отношение вытекает из непонимания того факта, что чисто эстетическое воспитание есть подготовка мозга к выполнению его самых тонких и высших функций. Мозг един. Модели, созданные в процессе эстетического воспитания, несомненно влияют на восприятие мира человеком, на его творческую деятельность. Как это происходит, в точности неизвестно. Тем ценнее эстетическое воспитание, ибо мы не знаем, чем его можно заменить.
Снова о понятиях
Начнем с фундаментальнейшего понятия логики — понятия «понятие». Выше (в главе 2) мы дали кибернетическое определение этого понятия в его аристотелевском варианте. Мы определили понятие как множество ситуаций на входе кибернетической системы. Владеть понятием — значит уметь его распознавать, т. е. уметь определить, принадлежит ли любая данная ситуация к множеству, характеризующему понятие, или не принадлежит. Это определение в равной степени относится и к сложным кибернетическим системам естественного происхождения, об устройстве которых мы имеем лишь общее представление (например, мозг животного), и к тем относительно простым системам, которые создаем мы сами с прикладными или исследовательскими целями.
В первом случае мы приходим к выводу, что система распознает некое понятие, на основе наблюдения за внешними проявлениями деятельности системы. Например, когда мы видим, что собака приходит в радостное возбуждение, заслышав голос хозяина, и совсем иначе реагирует на все остальные звуки, мы заключаем, что собака имеет понятие «голос хозяина». Это понятие вырабатывается у нее естественным путем, без каких-либо усилий со стороны экспериментатора. Чтобы выявить максимальные возможности мозга собаки, экспериментатор может ставить ее в необычайные условия и следить за ее реакцией. Много опытов такого рода было проведено И.П.Павловым и его школой. Если показать собаке фанерные круги и квадраты разного размера и цвета и после предъявления круга давать пищу, а после предъявления квадрата наказывать, то собака научится различать круг и квадрат и будет по-разному реагировать на предъявление этих фигур. Следовательно, собака способна распознавать некоторые общие (абстрактные) понятия, в данном случае — понятия круга и квадрата, отвлеченные от признаков размера и цвета. Значит, мы должны заключить, что собака владеет абстрактными понятиями «круг» и «квадрат».
Но, едва произнеся эту фразу, мы начинаем чувствовать, что такое заключение, пожалуй, было бы слишком поспешным. Утверждение, что собаке доступно понятие «голос хозяина» (имеется в виду, конечно, голос конкретного человека), можно принять без оговорок, но вот утверждение, что собаке доступно понятие квадрата, представляется в каком-то смысле верным, а в каком-то нет.
Заметим это себе, чтобы вернуться к этому вопросу позже. А пока завершим экскурс в область умственных способностей собаки указанием на простейшие понятия, которые собаке заведомо недоступны. Предположим, что вы показываете собаке ящик, разделенный на две части, в каждой из которых находится несколько биллиардных шаров. Вы хотите заставить ее отличить случай, когда число шаров в обеих частях одинаково, от случая, когда число шаров различно. Можно держать пари, вы не достигнете цели. Понятие равночисленности собаке недоступно.
Кибернетические системы, обладающие способностью распознавания понятий, создаются также искусственно. В связи с кибернетизацией науки и производства их значение непрерывно возрастает. Для понимания общих принципов и конкретных механизмов работы мозга разработка искусственных распознающих устройств играет решающую роль. Эти устройства служат моделями, с помощью которых люди пытаются приподнять завесу над процессом мышления. Создание «искусственного мозга», выполняющего хотя бы частично те же функции, что и естественный мозг, дает указания о том, как подходить к исследованию деятельности естественного мозга. Интересно, что одним из первых результатов сравнения искусственных и естественных распознающих систем был вывод о чрезвычайно узкой целенаправленности, специализации естественных систем. В рамках своей специализации они достигают высокого совершенства, но зато оказываются совершенно бессильными, когда задача выходит за эти рамки. Распознавание человека по голосу — чрезвычайно трудная задача для искусственных кибернетических устройств, а мозг собаки решает ее без труда. В то же время простейшая для искусственной системы задача сравнения числа биллиардных шаров непосильна для собаки.
В главе 2 мы рассматривали распознающее кибернетическое устройство, на вход которого подавались сигналы от светочувствительных рецепторов, расположенных на экране. Ситуацию, т. е. совокупность значений всех сигналов от рецепторов, мы называли «картинкой»; с точностью до полутонов она совпадает с изображением на экране.Это устройство (распознаватель картинок) послужит нам для иллюстраций и в настоящей главе.
Социальная интеграция
Метасистемный переход в системе мозга — управление ассоциированием — породил новый процесс — социальную интеграцию, т. е. объединение человеческих индивидуумов в некую целостность нового типа: человеческое общество. Вся история человечества проходит под знаком социальной интеграции, связи между людьми возрастают в количественном и качественном отношении. Этот процесс протекает и в настоящее время, причем весьма интенсивно, и вряд ли кто-либо может уверенно ответить на вопрос, как далеко он пойдет.
Социальная интеграция — это метасистемный переход, она приводит к новому уровню возникновения материи — социальной сфере. Сообщества животных можно рассматривать как первые (и безуспешные) попытки осуществить этот переход. Мы знаем сообщества животных, например муравьев, в которых отдельные особи настолько приспособлены к жизни в сообществе, что не могут жить вне его. Муравейник с полным правом можно назвать единым организмом, так далеко зашли в нем взаимодействие между особями и их специализация. Но это взаимодействие остается на уровне низших функций. «Контакта мозгов» нет. Создания новых моделей действительности нет. Никаких принципиально новых возможностей из-за объединения муравьев в общество не открывается, оно застывает в своем развитии. Муравейник, конечно, является метасистемой по отношению к отдельному муравью. Интеграция индивидуумов имеет место. Но это не новый этап эволюции, а боковое ответвление, тупик. В русской литературе сложилась традиция: слово' «социальное», которое буквально означает «общественное», относить только к человеческому обществу, подчеркивая этим его принципиальное отличие от общества животных. В этом смысле надо понимать термины «социальная сфера» и «социальная интеграция».
Итак, попытки природы образовать новый этап организации материи путем интеграции многоклеточных организмов долгое время не приводили к значительным результатам: не было подходящего материала. Понадобился метасистемный переход в структуре мозга, чтобы индивидуумы приобрели способность образовывать необходимые связи.
И еще одно следствие управления ассоциациями имеет важнейшее значение для развития социальной сферы — это способность человека выйти за рамки инстинкта, строить планы действий, никак с ним не связанные, а порой даже ему противоречащие. Эти два свойства делают человека социальным существом, т. е. материалом, пригодным для построения человеческого общества — социума. Слово «материал», сказанное о человеке, коробит; оно звучит как-то унизительно. В самом деле, разве есть какое-то высшее существо, которое строит общество, пользуясь человеком как материалом? Нет, конечно. Человек сам — творец. Причем не какой-то абстрактный Человек (с большой буквы), а конкретный человек, человеческая личность, индивидуум. Все, чем обладает общество, создано творчеством человеческих индивидуумов. А в то же время — такова диалектика отношения между личностью и обществом — человек значителен лишь постольку, поскольку он значителен для общества. Это, конечно, не надо понимать так, что кто не признан, тот не гений. Человек может выступать против всего общества, т. е. против всех живущих в данный момент людей, и руководствоваться в то же время интересами общества, логикой развития общества. Есть два уровня организации материи: уровень животного, для которого высшие законы — это инстинкты самосохранения и размножения, и уровень человека, т. е. человеческого общества. Все, что в человеке мы называем собственно человеческим, — продукт развития общества. Человек как чисто биологическое (в смысле досоциальное) существо — это лишь «возможность» человека в полном смысле слова, и не более. Если в действиях человека есть хоть какая-то логика, то это либо логика животных инстинктов, либо логика развития общества, быть может завуалированная и не осознаваемая в качестве таковой. Другой логике просто неоткуда взяться. Поэтому человек, выступая как творец, все-таки подчиняется хотя и не существу, но какому-то высшему закону эволюции Вселенной и, можно сказать, является материалом для его действия.
Соотношение неопределенностей
Квантовая механика разрушила это представление. Она была вынуждена это сделать под напором новых экспериментальных данных. Оказалось, что элементарные частицы ведут себя при определенных условиях не как частицы, а как волны, но при этом они не «размазываются» по большой области пространства, а сохраняют свои малые размеры и свою дискретность, размазывается же лишь вероятность их обнаружения в той или иной точке пространства.
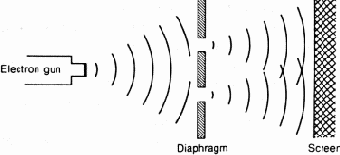
Рис. 13.1. Дифракция электронов
Рассмотрим в качестве иллюстрации рис. 13.1. На нем изображена электронная пушка, посылающая электроны определенного импульса на диафрагму, за которой расположен экран. Диафрагма сделана из непрозрачного для электронов материала, но имеет два отверстия, через которые электроны и попадают на экран. Экран покрыт веществом, которое светится под действием электронов, так что в том месте, куда попал электрон, происходит вспышка. Поток электронов из пушки достаточно редкий, так что каждый электрон проходит через диафрагму и фиксируется на экране независимо от других. Расстояние между отверстиями в диафрагме во много раз больше размеров электронов, полученных любыми оценками, но сравнимо по порядку с величиной h/p, где h — константа Планка, а p — импульс электрона, т. е. произведение его скорости на массу.
Таковы условия эксперимента. Результатом его является распределение вспышек на экране. Первый вывод из анализа результатов эксперимента таков: электроны попадают в различные точки экрана, и предсказать, в какую точку попадет каждый электрон, невозможно, можно только предсказать вероятность попадания в ту или иную точку, т. е. среднюю плотность вспышек после попадания в экран очень большого числа электронов.
Но это еще полбеды. Можно представить себе, что различные электроны пролетают в разных местах отверстий в диафрагме, испытывают различной силы влияния со стороны краев отверстий и поэтому отклоняются по-разному. Настоящие неприятности возникают тогда, когда мы начинаем исследовать среднюю плотность вспышек на экране и сравнивать ее с теми результатами, которые получаются, когда мы закрываем одно из отверстий в диафрагме.
Если электрон — это маленькая частица материи, то, попадая в район диафрагмы, он либо поглощается, либо проходит через одно из двух отверстий. Так как отверстия диафрагмы расположены симметрично относительно электронной пушки, в среднем половина электронов проходит через каждое отверстие. Значит, если мы закроем одно из отверстий и пропустим через диафрагму миллион электронов, а затем закроем второе отверстие, но откроем первое и пропустим еще миллион электронов, то мы должны получить такую же среднюю плотность вспышек, как если бы мы пропустили через диафрагму с двумя отверстиями два миллиона электронов. Но оказывается, что это не так! При двух отверстиях распределение получается иным, оно содержит максимумы и минимумы, как при дифракции волн.
Рассчитать среднюю плотность вспышек можно с помощью квантовой механики, связав с электронами так называемую волновую функцию, представляющую собой некое воображаемое поле, интенсивность которого пропорциональна вероятности наблюдаемых событий.
У нас отняло бы слишком много места описание всех попыток согласовать представление об электроне как об «обычной» частице (такие частицы стали называть классическими в отличие от квантовых) с экспериментальными данными об их поведении. Этому вопросу посвящена обширная литература, как специальная, так и популярная. Все такие попытки оказались безуспешными. Выяснились следующие две вещи.
Во-первых, если одновременно измеряется координата квантовой частицы (любой, не обязательно электронов) по некоторой оси х и импульс в этом направлении р, то ошибки измерения, которые мы обозначим через x; и p соответственно, подчиняются соотношению неопределенностей Гейзенберга:
?x × ?p
? h.
Никакими ухищрениями обойти это соотношение нельзя. Чем точнее мы пытаемся измерить координаты, тем больше оказывается разброс по величине импульса р, и наоборот. Соотношение неопределенностей есть универсальный закон природы, но, так как постоянная Планка h весьма мала, при измерениях с телами макроскопического размера оно роли не играет.
Во-вторых, представление о том, что на самом деле квантовые частицы движутся по каким-то вполне определенным траекториям, т. е. в каждый момент времени на самом деле имеют вполне определенные координату и скорость (а значит, и импульс), которые мы просто не можем точно измерить, наталкивается на непреодолимые логические трудности. Напротив, принципиальный отказ от приписывания квантовой частице реальной траектории и принятие положения, что самое полное описание состояния частиц — это задание ее волновой функции, приводят к логически безупречной, а математически простой и изящной теории, которая блестяще согласуется с экспериментальными фактами; в частности, из нее немедленно вытекает соотношение неопределенностей. Эта теория — квантовая механика. В уяснении физических и логических основ квантовой механики и в ее философском осмыслении главную роль сыграла деятельность крупнейшего ученого-философа нашего времени Нильса Бора (1885–1962).
Структурные и функциональные схемы
На структурной схеме кибернетической системы указывается, из каких подсистем состоит данная система. Часто указывается также, как направлены потоки информации между подсистемами. Тогда структурная схема превращается в граф. В математике называют графом систему точек (вершин графа), некоторые из которых соединены линиями (дугами). Граф называется ориентированным, если на каждой дуге указано определенное направление. Структурная схема с указанием потоков информации есть ориентированный граф, вершины которого изображают подсистемы, а дуги — потоки информации.
Такое описание кибернетической системы не является единственно возможным. Часто нас интересует не столько структура системы, сколько ее функционирование, действие. Еще чаще мы просто ничего не можем сказать толком о структуре, но кое-что можем сказать о функционировании. В таких случаях можно построить функциональную схему. Это тоже ориентированный граф, но вершины здесь изображают различные множества состояний системы, а дуги — возможные переходы между состояниями. Дуга соединяет две вершины в направлении от первой ко второй в том случае, если хотя бы из одного состояния, относящегося к первой вершине, возможен переход в какое-либо состояние, относящееся ко второй вершине. Множества состояний мы будем называть обобщенными состояниями. Следовательно, дуга на схеме указывает возможность перехода из одного обобщенного состояния в другое. Если структурная схема отражает главным образом пространственный аспект, то функциональная — главным образом временной. Формально в соответствии с данным выше определением функциональная схема вообще никак не отражает пространственного аспекта — разделения системы на подсистемы. Однако, как правило, разделение на подсистемы находит отражение в способе определения обобщенных состояний, т. е. разделения множества всех состояний системы на подмножества, «приписанные» к различным вершинам графа. Разберем это на примере системы, структурная схема которой представлена на рис. 2.12.
Это схема управления.
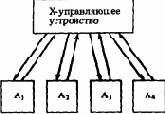
Рис. 2.12. Структурная схема управления
Одна из подсистем, называемая управляющим устройством, получает информацию от «рабочих» подсистем A1, A2, A3, …, перерабатывает ее и посылает подсистемам A1, A2, A3, … приказы (управляющую информацию), вследствие чего эти подсистемы меняют свое состояние. Надо отметить, что, строго говоря, любая информация меняет состояние системы, которая ее получает. Информацию называют управляющей в том случае, когда она меняет некоторые выделенные параметры системы, описываемые как «основные», «внешние», «наблюдаемые» и т. п. Часто бывает, что управляющее устройство по своей информационной емкости и пропускной способности невелико и служит лишь для переключения информационных потоков, а реальная обработка данных и выработка приказов производятся одной из подсистем A1, A2, A3, … или в соответствии с хранящейся в ней информацией. Тогда говорят, что управление переходит в эту подсистему. Так, в частности, обстоит дело в вычислительной машине, где A1, A2, A3, … — это ячейки оперативной памяти. Одни из ячеек содержат пассивную информацию (например, числа), другие — приказы (команды). Когда управление находится в ячейке, содержащей команду, управляющее устройство выполняет эту команду. Затем оно передает управление в другую ячейку и т. д.
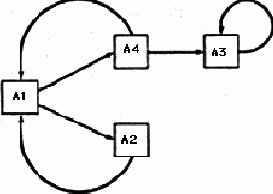
Рис. 2.13. Функциональная схема передачи управления
Для систем с передачей управления функциональную схему строят следующим образом. Каждой вершине графа сопоставляют одну из подсистем A, и множество всех состояний системы, при которых управление находится в данной подсистеме. Тогда дуги (стрелки) означают передачу управления от одной подсистемы к другой (рис. 2.13). На такой схеме даже при полной детерминированности каждого следующего состояния предыдущим могут быть разветвления благодаря тому, что каждая вершина соответствует обширному множеству состояний и передача управления может зависеть от состояния управляющего устройства или подсистемы, в которой находится управление.
Функциональные схемы часто рисуют обобщенно, пропуская какие-то несущественные детали и шаги. Тогда может оказаться, что то, по какому пути в разветвлении перейдет управление, зависит от состояния нескольких различных подсистем. Условие, при котором осуществляется данный переход, обычно выписывают рядом со стрелкой. Схему на рис. 2.10 можно понимать в таком именно смысле. Тогда в ней подразумевается, что система имеет две подсистемы: блок проверки и блок выполнения операции, и управление переходит из одной в другую в соответствии со стрелками. У системы могут быть и другие подсистемы (в данном случае — среда), но они никогда не получают управления и поэтому не изображаются на схеме (точнее, те моменты, когда среда меняет состояние системы или меняет свое состояние под действием системы, включаются в процесс действия одного из блоков).
Можно отойти еще дальше от структурной схемы. Передача управления в некоторую подсистему означает ее активацию, т. е. выполнение того действия, для которого подсистема предназначена. Но мы можем и не знать, какая подсистема отвечает за данное наблюдаемое действие. Тогда вершины графа мы будем отождествлять с действиями как таковыми, а другие будут означать переход от одного действия к другому. Понятие «действие как таковое», если определять его строго, надо отождествлять с понятием «обобщенное состояние» («множество состояний»), и это возвращает нас к первому — самому абстрактному — определению функциональной схемы. В самом деле, когда мы говорим, что собака «бежит», «лает» или «вертит хвостом», то под каждое из этих определений подходит множество конкретных состояний собаки. Правда, здесь бросается в глаза одна несообразность: «состояние» есть нечто статическое, в то время как «действие» — нечто явно динамическое, скорее изменение состояния, чем само состояние. Если на мгновенной фотографии хвост собаки не выходит из плоскости симметрии, то еще неизвестно, вертит она им или он застыл в неподвижности. Это противоречие снимается тем замечанием, что в понятие состояния входят не только величины типа «положение», но и величины типа «скорость», «ускорение» и т.д. В частности, указание состояния собаки включает указание напряженности мышц ее хвоста и возбужденности всех нейронов, регулирующих состояние мышц.
Структурный подход
Логическое понятие мы определяем как элемент функционирования языковой системы. Теперь мы попытаемся дать общее определение кибернетического понятия «понятие», опираясь не на функциональный, а на структурный подход.
Рассмотрим снова понятие «внутри» в приложении к распознавателю картинок. Как мы стали бы строить систему, имеющую понятие «внутри»? Очевидно, сначала мы должны были бы сконструировать классификаторы для понятий «пятно» и «контур». Напомним, что классификатор — это кибернетическая система, которая распознает принадлежность входного состояния (ситуации) к определенному множеству (аристотелевскому понятию) и перерабатывает его в выходное состояние, отражающее важнейшие характеристики ситуации. Например, классификатор пятна распознает наличие пятна и фиксирует координаты точек, ограничивающие его. На рис. 7.4 мы обозначили П1, П2,... и K1, K2,... классификаторы пятен и контуров соответственно. Эти классификаторы образуют первый уровень иерархии, ибо их вход — состояние рецепторов. Они переводят ситуации с языка светящихся точек на язык пятен и контуров.
Построив первый уровень, мы принимаемся за второй. Мы конструируем классификатор В (см. рис. 7.4), на вход которого подается выход одного классификатора пятна, пусть это будет Пi, и одного классификатора контура Кj. Выходных состояний у классификатора В должно быть всего два: одно («да») наступает, когда пятно, фиксируемое классификатором Пi, лежит внутри контура, фиксируемого классификатором Кj, а второе («нет») — в противном случае. Нам хотелось бы, чтобы классификатор В можно было бы применить к любой паре (Пi, Кj). Но было бы безумием делать столько экземпляров В, сколько есть пар (Пi, Кj)! Поэтому нам необходим какой-то переключатель, с помощью которого на одно-единственное устройство В можно было бы подать информацию из разных точек системы. Так как бессмысленно подавать на классификатор информацию непосредственно от рецепторов или из каких-либо других неподходящих точек, переключатель следует сконструировать таким образом, чтобы он мог подать информацию от любой из пар (Пi, Кj) и никак иначе.
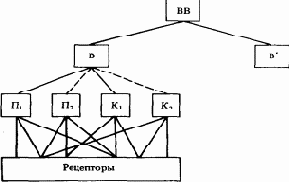
П — пятно, К — контур, В — внутри, ВВ — войти внутри.
Рис. 7.4. Иерархия классификаторов
Классификатор В расположен на втором уровне системы в целом. Возможно, что он будет использован в качестве входа для третьего уровня. Допустим, например, что от системы требуется распознать понятие «войти в...» Это понятие динамическое, оно связано с временем. В качестве входа здесь надо рассматривать не одну ситуацию, а их последовательность, то, что было выше названо кинолентой ситуаций. При наличии такой киноленты мы говорим, что пятно «вошло в» контур, если сначала оно было вне контура, а потом стало внутри него. Очевидно, распознаватель понятия «войти в» (на рис. 7.4 он обозначен ВВ ) будет на своем входе требовать выхода от распознавателя В или нескольких распознавателей В, относящихся к различным кадрам киноленты (в первом случае он должен иметь устройство для хранения последовательности ответов «да» или «нет»).
Получилась иерархия классификаторов. Это для нас не ново, мы уже рассматривали иерархию классификаторов в главе 2. Но в главе 2 мы ограничивались аристотелевскими понятиями, при этом иерархия классификаторов выступала только как средство распознавания понятий и не входила в определение понятия «понятие». Понятие «понятие» (аристотелевское) мы определили независимо от устройства иерархии классификаторов как некоторое множество ситуаций, иначе говоря, как функцию, принимающую истинное значение «верно» на данном множестве ситуаций.
Теперь же, ища кибернетическое истолкование таких понятий, как «внутри», мы видим, что не можем определить общее понятие «понятие», опираясь только на уровень рецепторов, а можем определить его лишь как элемент системы понятий. Понятию «внутри» соответствует на рис. 7.4 классификатор В не только как устройство, перерабатывающее данный вход в данный выход, но и как подсистема всей системы распознавания, т. е. как элемент, связанный определенным образом с другими элементами системы (в данном случае получивший входную информацию от одного классификатора типа П и одного классификатора типа К).
Мы построили кибернетическую модель понятия «внутри». Но как связана эта модель с действительностью? Какое отношение она имеет к настоящему понятию «внутри», которое проявляется в языке и представляется нам одним из элементов нашего мышления? Можно ли утверждать, что в мозгу есть классификатор, в точности соответствующий этому понятию? Хотя общий вид схемы на рис. 7.4 — наличие рецепторов и классификаторов — отражает нейрофизиологические данные, конкретные функции классификаторов и взаимосвязь между ними отражают данные логики. Поэтому наша схема — не модель устройства, мозга, а модель функционирования языковой системы, точнее структурная схема устройства, которое могло бы выполнять функции, обнаруживаемые в языковой деятельности. В этом устройстве классификаторы выполняют функции, описываемые логическими понятиями, а переключатели (на схеме не показаны, но в тексте упоминались) фиксируют область определения понятий.
Схему на рис. 7.4 можно воплотить в реальном кибернетическом устройстве, для которого источником информации будут светящиеся точки экрана. Но, если такое устройство будет работать даже очень хорошо, это еще не дает нам, строго говоря, права считать его моделью устройства мозга. Быть может, то расчленение нервных сетей на классификаторы, которое подсказывает рис. 7.4, или аналогичные схемы, взятые из функционирования языка, совершенно не отражают истинного устройства мозга!
Субстанция
Среднеевропейский стандарт имеет два вида существительных, обозначающих материальные части окружающего нас мира. Существительные первой группы: «a tree — дерево», «a stick — палка», «a man — мужчина» и т. п. — относятся к отдельным предметам, имеющим определенную форму. Существительные второй группы: «water — вода», «milk — молоко», «meat — мясо» — обозначают однородную массу, не имеющую определенных границ. Между этими группами существует весьма четкое грамматическое различие: у существительных, обозначающих вещества, нет множественного числа; в английском языке перед ними опускается артикль, во французском языке ставится партитивный артикль. Однако если вдуматься в смысл различия между этими двумя видами предметов, то станет ясно, что в действительности они не отличаются друг от друга так четко, как в языке, а пожалуй, и вообще ничем не отличаются. И вода, и молоко, и мясо встречаются в природе только в виде больших или малых тел определенной формы. Различие между двумя группами существительных навязывается нам языком и часто оказывается столь неудобным, что приходится пользоваться такими конструкциями, как «кусок мяса» или «стакан воды», хотя слово «кусок» не указывает никакой определенной формы, а слово «стакан» хотя и предполагает определенную форму, но тем самым вносит только путаницу, ибо, говоря «стакан воды», мы имеем в виду лишь количество воды, но не форму ее в сосуде. Наш язык нисколько не потерял бы в изобразительной силе, если бы слово «мясо» обозначало кусок мяса, слово «вода» — некоторое количество воды.
Именно так обстоит дело в языке хопи. Все существительные обозначают у них отдельные предметы и имеют единственное и множественное число. Существительные, которые мы переводим как существительные второй группы (вещества) относятся к телам, у которых форма и размеры не отсутствуют, а просто не указываются, игнорируются в процессе абстракции подобно тому, как в понятии « камень» отсутствует указание на форму, в понятии «шар» — на размер.
Поэтому понятие субстанции как чего-то, имеющего материальное бытие и в то же время принципиально не имеющего никакой формы, не могло бы, по-видимому, возникнуть у хопи и быть понятым человеком, говорящим только на языке хопи. В европейской культуре понятие субстанции возникает как обобщение понятий, выражаемых существительными второй группы, в то время как обобщение понятий, выражаемых существительными первой группы, приводит к понятию предмета. Для хопи, в языке которого деления существительных на две группы нет, возможно только одно обобщение и оно, конечно, приводит к понятию предмета (или тела), ибо можно отвлечься от формы наблюдаемого материального объекта, но нельзя сказать, что она не существует. Мысленно расчленение всего сущего на некую нематериальную форму и материальное, но бесформенное содержание (субстанцию), столь характерное для традиционной европейской философии, покажется, вероятно, хопи надуманным и ненужным. И он будет прав! (Это уже замечание не Уорфа, а автора настоящей книги.) Понятие субстанции, игравшее такую важную роль в спорах средневековых схоластов, совершенно исчезло из современной науки.
о которых мы говорили выше,
Успехи квантовой механики, о которых мы говорили выше, относятся главным образом к описанию нерелятивистских частиц, т. е. частиц, движущихся со скоростями, много меньшими, чем скорость света, так что эффектами, связанными с теорией относительности (релятивистскими эффектами), можно пренебречь. Именно нерелятивистскую квантовую механику мы имели в виду, когда говорили о ее полноте и логической стройности. Нерелятивистская квантовая механика достаточна для описания явлений атомного уровня, но физика элементарных частиц высоких энергий требует создания теории, совмещающей идеи квантовой механики и теории относительности. До сих пор на этом пути достигнуты лишь частичные успехи; единой и последовательной теории элементарных частиц, объясняющей огромный материал, накопленный экспериментаторами, не существует. Попытки построить новую теорию путем непринципиальных исправлений старой теории не приводят к значительным результатам. Создание удовлетворительной теории элементарных частиц упирается в чрезвычайную своеобразность этой области явлений, происходящих как бы в совсем ином мире и требующих для своего описания совершенно необычных понятий, в самой основе расходящихся с привычной нам понятной схемой.
В конце 50-х годов Гейзенберг предложил новую теорию элементарных частиц, ознакомившись с которой Бор сказал, что она вряд ли окажется верной, потому что она «недостаточно сумасшедшая». Теория действительно не получила признания, а меткое замечание Бора стало известно всем физикам и даже попало в популярную литературу. Словечко «сумасшедшая» естественным образом ассоциировалось с эпитетом «странный», применяемым к миру элементарных частиц. Но означает ли «сумасшедшая» только «странная», «необычная»? Пожалуй, если бы Бор сказал «недостаточно необычная», афоризма не получилось бы. Слово «сумасшедшая» вносит оттенок «шальная», «взявшаяся неизвестно откуда» и блестяще характеризует нынешнюю ситуацию в теории элементарных частиц, когда всеми признается необходимость глубокой перестройки теории, но, как к ней приступить, неизвестно.
Возникает вопрос: неужели «странность» мира элементарных частиц, неприменимость к нему нашей интуиции, выработанной в макромире, обрекает нас отныне и навечно на блуждание в темноте?
Вдумаемся в природу возникших трудностей. Принцип создания формализованных языковых моделей действительности не пострадал при переходе к изучению микромира. Но если колесики этих моделей — физические понятия — брались в своей основе из нашего повседневного макроскопического опыта и лишь уточнялись путем формализации, то для нового «странного» мира нужны новые «странные» понятия, которые взять неоткуда и которые придется, следовательно, изготовлять заново, да еще и соединить их должным образом в целостную схему. На первом этапе исследования микромира одно из таких колесиков — волновая функция нерелятивистской квантовой механики — было изготовлено сравнительно легко, опираясь на уже существовавший математический аппарат, служивший для описания макроскопических явлений (механика материальной точки, механика сплошных сред, теория матриц). Физикам просто повезло: они нашли прообразы необходимого им колесика в двух (совершенно различных) колесиках макроскопической физики и составили из них «кентавра» — квантовое понятие волны-частицы.
Однако нельзя все время рассчитывать на везение. Чем глубже мы проникаем в микромир, тем сильнее отличаются необходимые понятия-конструкты от привычных понятий макроскопического опыта и тем меньше вероятность соорудить их с ходу, без всяких инструментов, без всякой теории. Следовательно, мы должны подвергнуть научному анализу саму задачу построения научных понятий и теорий, т. е. совершить очередной метасистемный переход. Чтобы квалифицированно построить определенную физическую теорию, нам нужна общая теория построения физических теорий (метатеория), в свете которой прояснится путь решения нашей конкретной задачи. Сравнение наглядных моделей старой физики с лошадью, а абстрактных знаковых моделей с паровозом, можно развить следующим образом. Лошади предоставлены в наше распоряжение природой.
Они растут и размножаются сами по себе, и чтобы использовать их, не нужно знать их внутреннее устройство. Но паровоз мы должны построить сами. Для этого мы должны понять принципы его устройства и физические законы, лежащие в их основе, а также иметь какие-то инструменты для работы. Пытаясь построить теорию «странного» мира, не имея метатеории физических теорий, мы уподобляемся человеку, который задумал построить паровоз голыми руками или построить самолет, не имея представления о законах аэродинамики.
Итак, созрел очередной метасистемный переход. Физика требует... хочется сказать «метафизики», но, к счастью для нашей терминологии, нужная нам метатеория является таковой по отношению к любой естественнонаучной теории, имеющей высокую степень формализации, поэтому ее правильнее назвать метанаукой. Этот термин обладает тем недостатком, что создает впечатление, будто метанаука есть нечто, принципиально лежащее вне науки, в то время как в действительности новый уровень иерархии, создаваемый этим метасистемным переходом, надо, конечно, включить и в общее тело науки, расширяя тем самым это тело. Ситуация здесь такая же, как с термином метаматематика; ведь метаматематика — это тоже часть математики. Но поскольку термин «метаматематика» был все-таки принят, можно считать приемлемым и термин «метанаука». Впрочем, поскольку важнейшая часть метанаучного исследования — исследование понятий теории, можно предложить также термин концептология.
Основную задачу метанауки можно сформулировать так. Дана некая совокупность или некий генератор фактов. Каким образом построить теорию, эффективно описывающую эти факты и делающую правильные предсказания?
Если мы хотим, чтобы метанаука вышла за рамки общих рассуждений, то надо строить ее как полноценную математическую теорию, а для этого ее объект — естественнонаучная теория — должен предстать в формализованном (пускай упрощенном — такова цена формализации) виде, подвластном математике. Представленная в таком виде научная теория есть формализованная языковая модель, механизм которой составляет иерархическая система понятий — точка зрения, которую мы приводили на протяжении всей книги.
С этой точки зрения создание математической метанауки представляется очередным и естественным метасистемным переходом, совершая который мы делаем предметом изучения формализованные языки в целом, причем не только в отношении их синтаксиса, но также — и главным образом — с точки зрения семантики, с точки зрения их приложения к описанию действительности. К этому шагу нас подводит весь путь развития физико-математической науки.
Впрочем, до сих пор мы в своих рассуждениях исходили из потребностей физики. А как обстоит дело с точки зрения чистой математики?
Если физики-теоретики знают, что им нужно, но сделать могут немного, то «чистых» математиков можно, скорее, упрекнуть в том, что они сделать могут много, но не знают, что им нужно. Нет спору, многие чисто математические работы нужны для придания связности и стройности всему зданию математики, и смешно было бы требовать от каждой работы немедленных «практических» приложений. Но все-таки математика создается для познания действительности, а не с эстетическими или спортивными целями, подобно шахматам, и даже самые высокие ее этажи нужны, в конечном счете, лишь постольку, поскольку они способствуют достижению этой цели.
Вероятно, рост здания математики ввысь нужен всегда и представляет собой безусловную ценность. Но математика разрастается также и вширь, и все труднее становится определить, что не нужно, а что нужно, и если нужно, то в какой степени. Математическая техника развита сейчас настолько, что сконструировать в рамках аксиоматического метода несколько новых математических объектов и исследовать их свойства стало чуть ли не таким же обыкновенным, хотя и не всегда легким делом, как для древнеегипетских писцов произвести вычисления над дробями. Но, кто знает, понадобятся ли эти объекты? Возникает потребность в теории приложения математики, а это по существу и есть метанаука. Следовательно, развитие метанауки — это направляющая и организующая задача по отношению к более конкретным математическим задачам.
До создания эффективной метанауки пока еще далеко.
Сейчас трудно представить даже ее общие контуры. Чтобы они прояснились, необходимо выполнить еще много подготовительных работ. Физики должны овладеть «бурбакизмом», прочувствовать игру математических структур, которая приводит к возникновению богатых аксиоматических теорий, пригодных для детального описания реальности. Они должны вместе с математиками научиться раскладывать знаковые модели на отдельные кирпичики, чтобы складывать из них нужные им блоки. И, конечно, необходимо развитие техники проведения формальных выкладок над произвольными символьными выражениями (а не только числами) с помощью электронных вычислительных машин. Подобно тому, как переход от арифметики к алгебре происходит только после полного освоения техники арифметических вычислений, так и переход к теории создания произвольных символьных систем требует высокой техники действий над символьными выражениями, требует практического снятия проблемы выполнения громоздких формальных выкладок. Внесут ли новые методы вклад в разрешение тех конкретных трудностей, которые стоят сейчас перед теорией элементарных частиц, или же они будут раньше разрешены ручными, «дедовскими» методами, неизвестно, да это, в конце концов, и не важно, ибо, несомненно, появятся новые трудности. Так или иначе, вопрос о создании метанауки стоит на повестке дня. Рано или поздно он должен быть решен, и тогда люди получат новое оружие для покорения самых странных фантастических миров.
1 Bacon F. Novum Organum, Great books of the western world. Encyclopedia Britannica, 1955. Aphorism 95. P. 126.
2 Bacon F. Ор. cit. Aphorism 117. Р. 131.
3 Cм. сборник: Эйнштейн А. Физика и реальность. М.: Наука, 1965. Следующие ниже цитаты взяты также из этого сборника.
4 Frank P. Philosophy of science. Englewood Cliffs (New Jersey): Prentice-Hall, 1957.
5 Лаплас П. Опыт философии теории вероятностей. М., 1908. С. 9.
6 Этот раздел написан по мотивам статьи автора под таким же названием, опубликованной в журнале «Вопросы философии», 1968. N5.
Сваи, уходящие вглубь
Описание математических аксиом как моделей действительности, которые истинны не только в сфере реального опыта, но и в сфере воображения, опирается на их субъективное восприятие. Можно ли дать им более объективную характеристику. Воображение возникает на определенном этапе развития нервной системы как произвольное ассоциирование представлений. Предыдущим этапом был этап непроизвольного ассоциирования (уровень собаки). Естественно предположить, что переход от непроизвольного ассоциирования к произвольному не произвел существенной перемены в том материале, который имеется в распоряжении ассоциирующей системы, т. е. в представлениях, образующих ассоциации,— это следует из иерархического принципа устройства и развития нервной системы, при котором надстройка верхних этажей слабо влияет на нижние. Из того же принципа следует, что в процессе предыдущего перехода — от фиксированных понятий к непроизвольному ассоциированию — самые нижние уровни системы понятий остались неизменными и обусловили те всеобщие глубокие свойства представлений, которые были в наличии и до ассоциирования и которые ассоциирование изменить не может. Не может изменить их и воображение. Эти свойства инвариантны относительно преобразований, осуществляемых воображением. На них-то и опираются математические аксиомы. Если представить себе деятельность воображения как перетасовку и склейку каких-то элементов, «кусков» чувственного восприятия, то аксиомы — это модели, которые истинны для каждого куска и поэтому — для любой их комбинации. Способность воображения разрезать чувственный опыт на куски не безгранична, ибо, возникая на некотором этапе развития, оно принимает уже существующую систему понятий как некий фон, как основу, не подлежащую переделке. Такие глубокие понятия, как движение, тождество, непрерывность, заложены были в этом фоне, поэтому и модели, опирающиеся на эти понятия, оказываются универсально истинными не только для реального опыта, но и для любых конструкций, которые способно создать воображение.
Математика образует каркас здания естественных наук. Ее аксиомы — это сваи, уходящие в самую глубь нейронных понятий, ниже того уровня, где начинает хозяйничать воображение. Отсюда та прочность основы, которая отличает математику от эмпирического знания. Она пренебрегает поверхностными ассоциациями, составляющими каждодневный жизненный опыт, предпочитая продолжать строительство костяка системы понятий, начатого природой и заложенного в нижние уровни иерархии. И уже на этом костяке будут образовываться «необязательные» модели, которые мы относим к естественным наукам, как на базе врожденных и «обязательных» понятий низшего уровня образуются «необязательные» ассоциации представлений, составляющие содержание жизненного опыта. Требования, диктуемые математикой, обязательны; строя модели действительности, мы не можем обойти их, если бы даже захотели. Поэтому возможную неистинность теории мы всегда выносим за пределы сферы действия математики. Если обнаруживается расхождение между теорией и экспериментом, изменяют внешнюю, «необязательную» часть теории, но никому не приходит в голову высказать предположение, что в данном случае оказалось неверным равенство 2 + 2 = 4.
«Обязательность» классических математических моделей не противоречит появлению математических и физических теорий, которые, на первый взгляд, вступают в конфликт с нашей пространственно-временной интуицией (например, неевклидова геометрия или квантовая механика). Эти теории суть языковые модели действительности, полезность которых проявляется не в сфере повседневного опыта, а в весьма специальных ситуациях. Они не разрушают и не заменяют классических моделей, а продолжают их. Так, квантовая механика опирается на классическую. А какая теория может обойтись без арифметики? Парадоксы и противоречия возникают тогда, когда мы забываем, что понятия-конструкты, входящие в новую теорию, это — новые понятия, если даже их обозначают старыми именами. Мы говорим о «прямой» в неевклидовой геометрии и называем электрон «частицей», хотя языковая деятельность, связанная с этими словами, — доказательство теорем и квантово-механические выкладки — совсем не такая, как в прежних теориях, из которых были заимствованы термины.
Если дважды два не равно четырем, то либо два — не два, либо «жды» — не «жды», либо четыре — не четыре.
Особую роль математики в процессе познания можно выразить в виде утверждения, что математические понятия и аксиомы представляют собой не результат, а условие и форму познания действительности. Эта мысль была развита Кантом, и с ней можно согласиться, если рассматривать человека как полностью данное существо и не задавать себе вопроса: а почему человеку свойственны эти условия и формы познания? Но, задав этот вопрос, мы должны прийти к выводу, что они сами являются моделями действительности, выработанными в процессе эволюции (который в одном из важных своих аспектов есть не что иное, как процесс познания мира живыми структурами). С точки зрения законов природы принципиальной разницы между математическими и эмпирическими моделями нет; это разграничение отражает лишь наличие в устройстве человеческого мозга черты, отделяющей врожденные модели от благоприобретенных. Положение этой черты, надо полагать, содержит элемент исторической случайности. Проходи она в другом уровне, мы, возможно, были бы не в силах вообразить, что солнце может не взойти или что человек может парить над землей, как будто силы тяжести не существует.
Сверхсущество
Возникновение человеческого общества — крупномасштабный метасистемный переход, при котором интегрируемые подсистемы — это целые организмы. В этом плане его можно сравнить с возникновением многоклеточных организмов из одноклеточных. Однако его значение, его революционность неизмеримо больше. И если с чем-то сравнить его, то только с самим актом возникновения жизни. Ибо появление человека означает появление нового механизма усложнения организации материи, нового механизма эволюции Вселенной. До человека развитие и усовершенствование высшего уровня организации — устройства мозга — происходили лишь в результате борьбы за существование и естественного отбора. Это медленный процесс, требующий смены многих поколений. В человеческом обществе развитие языка и культуры является результатом творческих усилий всех его членов. Отбор вариантов, необходимый для усложнения организации материи по методу проб и ошибок, происходит теперь в голове человека. Он может происходить на уровне интуиции, представляясь результатом внезапного озарения, вдохновения, а может и распадаться на отдельные, отчетливо осознаваемые шаги; но так или иначе он становится неотделимым от волевого акта человеческой личности. Этот процесс существенно отличается от процесса естественного отбора и протекает несравненно более быстро, но по своей функции — построение и использование моделей окружающей среды — и по своим результатам — возрастание обшей массы живого вещества и его влияние на неживое — он полностью аналогичен первому процессу, он является его естественным продолжением. Человек становится сосредоточием Космического Творчества. Темп эволюции многократно возрастает.
Можно рассматривать общество как единое сверхсущество. Его «тело» — это тела всех людей плюс предметы, созданные и создаваемые людьми: одежда, жилища, машины, книги и т. д. Его «физиология» — это физиология всех людей плюс культура общества, т. е. определенный способ управлять предметным компонентом общественного тела и образом мышления людей.
Возникновение и развитие человеческого общества знаменуют начало нового (седьмого по нашему счету) этапа эволюции жизни (рис. 4.2). Функциональная формула метасистемного перехода от шестого к седьмому этапу такова:
Управление мышлением = Культура.
Язык входит в культуру в качестве важнейшей составной части, выполняя функции нервной системы. Как и у нервной системы многоклеточного организма, его первая, исторически и логически, функция — коммуникативная — обмен информацией между подсистемами, координация их деятельности. В процессе выполнения этой функции язык — опять-таки в точности так же, как и нервная система «этажом ниже», — получает вторую функцию — моделирование окружающей среды. И подобно тому, как в развитии мозга можно выделить этапы, связанные с метасистемными переходами, развитие языковых моделей происходит (как мы увидим дальше) путем последовательных метасистемных переходов в структуре языка.
|
Химическая эра |
1. Химические основы жизни |
|
2. Движение |
|
|
3. Раздражимость (простой рефлекс) |
|
|
Кибернетическая эра |
|
|
4. Нервная сеть (сложный рефлекс) |
|
|
5. Ассоциирование (условный рефлекс) |
|
|
Эра разума |
6. Мышление |
|
7. Социальная интеграция, культура |
Параллели между обществом и многоклеточным организмом были подмечены давно. Но вот вопрос: как относиться к этим параллелям? Можно считать их если и не случайными, то, во всяком случае, поверхностными и малозначительными, что-то вроде сходства стрелы подъемного крана с руками человека. Однако кибернетический подход приводит нас к другой точке зрения, согласно которой аналогия между обществом и организмом имеет глубокий смысл, свидетельствуя о наличии чрезвычайно общих законов эволюции, действующих на всех уровнях организации материи, и указывая нам направление развития общества. Эта точка зрения таит в себе ту угрозу, что, будучи вульгаризована, она легко может привести к концепции тоталитарного государства фашистского типа. В главе 14, рассматривая проблему творческой свободы личности, мы более подробно рассмотрим и этот вопрос. А пока отметим, что возможность вульгаризации теории никак не может быть аргументом против ее истинности. Раздел современной науки, именуемый кибернетикой, дает нам понятия, описывающие эволюционный процесс как на уровне внутриклеточных структур, так и на уровне социальных явлений. Фундаментальное единство эволюционного процесса на всех уровнях организации превращается из философского воззрения в научно обоснованный факт. С ним нельзя не считаться, размышляя о судьбах человечества и его роли во Вселенной.
Подчеркивая космическое значение разума, французские ученые Леруа и Тейяр де Шарден ввели термин ноосфера (т. е. сфера разума) для обозначения той части биосферы, где господствует разум. Эти идеи были подхвачены нашим соотечественником В.П.Вернадским (см. его статью «Несколько слов о ноосфере»). В предисловии к своему главному сочинению «Феномен человека» Тейяр де Шарден пишет:
Я думаю, вряд ли у мыслящего существа бывает более великая минута, чем та, когда с глаз его спадает пелена и открывается, что он не затерянная в космическом безмолвии частица, а пункт сосредоточения и гоминизации универсального стремления к жизни. Человек — не статический центр мира, как он долго полагал, а ось и вершина эволюции, что много прекраснее1.
1 Тейяр де Шарден П. Феномен человека. М.: Наука, 1987.