Строим икосаэдр

Для иллюстрации работы с массивами вершин создадим более сложный объект — икосаэдр. Это такой дссятистенный дом с острой пятиугольной крышей и таким же полом, но углы пола смещены (повернуты) на л/5 относительно углов потолка.

Икосаэдр имеет 20 треугольных граней и 12 вершин (1 + 5 на потолке и 1 + 5 на полу). Благодаря своей правильности он может быть задан с помощью всего лишь двух чисел, которые лучше вычислить один раз и запомнить. Этими числами является косинус и синус угла в три пятых окружности, то есть

static double

//======

atan(l.) - это пи/4

angle = 3. * atan(1.)/2.5, //====== 2 характерные точки

V = cos(angle), W = sin(angle);

Этот код мы вставим внутрь функции рисования, чтобы не плодить глобальные переменные и не нарываться на конфликты имен. Вот новая версия функции DrawScene:

void DrawScene() { static double

//====== 2 характерные точки

angle = 3. * atan(l.)/2.5, V = cos(angle), W = sin(angle),

//=== 20 граней икосаэдра, заданные индексами вершин

static GLuint id[20][3] =

//====== Начинаем формировать список команд

glNewList (1,GL_COMPILE) ;

//====== Выбираем текущий цвет рисования

glColor3d (1., 0.4, 1 . ) ;

glBegin (GLJTRIANGLES) ;

for (int i = 0; i < 20; i++)

{

//====== Грубый подход к вычислению нормалей

glNorma!3dv(v[id[i] [0] ] ) ;

glVertex3dv(v[id[i] [0] ] ) ;

glNorma!3dv(v[id[i] [1] ] ) ;

glVertex3dv(v[id[i] [1] ] ) ;

glNorma!3dv(v[id[i] [2] ] ) ;

glVertex3dv(v[id[i] [2] ] ) ;

}

glEnd() ;

//====== Конец списка команд

glEndList ();

}

Точное вычисление нормалей

Проверьте результат и обсудите качество. В данном варианте нормали в вершинах заданы так, как будто изображаемой фигурой является сфера, а не икосаэдр. Это достаточно грубое приближение. Если поверхность произвольного вида составлена из треугольников, то вектор нормали к поверхности каждого из них можно вычислить точно, опираясь на данные о координатах вершин треугольника. Из $ курса векторной алгебры вы, вероятно, помните, что векторное произведение двух векторов а и b определяется как вектор п, перпендикулярный к плоскости, в которой лежат исходные векторы. Величина его равна площади параллелограмма, построенного на векторах а и b как на сторонах, а направление определяется так, что векторы a, b и п образуют правую тройку. Последнее означает, что если представить наблюдателя на конце вектора п, то он видит поворот вектора а к вектору b, совершаемый по кратчайшему пути против часовой стрелки. На рис. 6.4. изображена нормаль п (правая тройка) при различной ориентации перемножаемых векторов а и b.

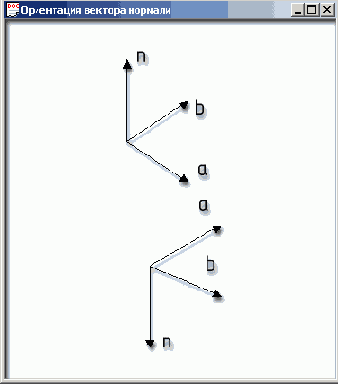
Рис. 6.2. Ориентация вектора нормали

Если координаты векторов а и b известны, то координаты нормали вычисляю по следующим формулам. Длина вектора нормали п зависит от длин вектор сомножителей и величины угла между ними:

Nx=AxBz-AzBy

Ny=AzBx-AxBz

Nz=AxBy-AyBx

Примечание

Можно потерять много времени на осознание того факта, что не только правление нормали, но и ее модуль влияют на величину освещенности (и та) вершины, так как сопровождающая документация (Help) не содер; явных указаний на это. Отметьте также, что цвета вершин полигона влияю цвета точек заполнения полигона, так как цвета вновь генерируемых то интерполируются, то есть принимают промежуточные значения между з чениями цвета вершин.

Чтобы нивелировать зависимость цвета вершины от амплитуды нормали, обыч вектор нормали масштабируют (или нормируют), то есть делают его длину р; ной единице, оставляя неизменным направление. С учетом сказанного создал две вспомогательные функции. Первая масштабирует, а вторая вычисляет н< маль к плоскости треугольника. Алгоритм вычисления использует координа двух сторон, прилегающих к текущей вершине треугольника:

//====Нормирование вектора нормали (или любого другого)

void Scale(double v[3])

{

double d = sqrt(v[0]*v[0]+v[l]*v[l]+v[2]*v[2]);

if (d == 0.)

{

MessageBox(0,"Zero length vector","Error",MB_OK);

return;

}

void getNorm(double vl[3], double v2[3], double out[3])

{

//===== Вычисляем координаты вектора нормали

//====== по формулам векторного произведения

out[0] = vl[l]*v2[2] - vl[2]*v2[l];

out[l] = vl[2]*v2(0] - vl[0]*v2[2] ;

out[2] =vl[0]*v2[l] - vl[l]*v2[0];

Scale(out);

}

Замените функцию DrawScene. В новом варианте мы аккуратно вычисляем и масштабируем нормали в каждом из двадцати треугольников поверхности икосаэдра:

void DrawScene()

{

static double

angle - 3. * atanfl.)/2.5, V = cos(angle), W = sin(angle),

v[12] [3] = {

{-V,0.,W}, {V,0.,W}, {-V,0.,-W},

{V,0.,-W}, {0.,W,V}, {0.,W,-V},

{0.,-W,V}, {0. ,-W,-V}, {W,V, 0.},

{-W,V,0.}, {W,-V,0.}, {-W,-V,0.}

};

static GLuint id[20][3] = {

(0,1, 4), {0,4, 9}, (9,4, 5), (4,8, 5}, (4,1,8),

(8,1,10), (8,10,3), (5,8, 3), (5,3, 2), (2,3,7),

(7,3,10), (7,10,6), (7,6,11), (11,6,0), (0,6,1),

(6,10,1), (9,11,0), (9,2,11), (9,5, 2), (7,11,2) 1;

glNewList(l,GL_COMPILE); glColorSd (1., 0.4, 1.) ;

glBegin(GLJTRIANGLES);

for (int i = 0; i < 20; i++)

{

double dl[3], d2[3], norm[3];

for (int j = 0; j < 3; j++)

{

dl[j] =v[id[i][0]] [j] -v[id[i][l]J [j];

d2[j] =v[id[i][l]] [j] -v[id[i][2J] [j];

}

//====== Вычисление и масштабирование нормали

getNorm(dl, d2, norm);

glNormal3dv(norm);

glVertexSdv(v [ id[i] [1]]);

glVertex3dv(v[id[i] [1] ] glVertex3dv(v[id[i] [2] ]

glEnd() ;

}

glEndList () ;

}

Примечание

Функцию нормировки всех нормалей можно возложить на автомат OpenGL, если включить состояние GL_NORMALIZE, но обычно это ведет к замедлению перерисовки и, как следствие, выполнения приложения, если изображение достаточно сложное. В нашем случае оно просто, и поэтому вы можете проверить действие настройки, если вставите вызов glEnable (GL_NORMALIZE); в функцию Init (до вызова OrawScene) и временно выключите вызов Scale(out); производимый в функции getNorm. Затем вернитесь к исходному состоянию.

Содержание раздела