|
|
Как
создать сферу
Для того чтобы
из существующей заготовки — икосаэдра из двадцати граней — создать сферу, круглую,
блестящую и без изъянов, нужно осуществить предельный переход, как в матанализе,
бесконечно увеличивая число треугольников при бесконечном уменьшении их размеров.
В дискретном мире нет места предельным переходам, поэтому вместо бесконечного
деления надо ограничиться каким-то конечным числом и начать делить каждый из
двадцати треугольников икосаэдра на все более мелкие правильные треугольники.
Вычисление нормали при этом упрощается, так как при приближении к шару нормаль
в каждой вершине треугольника приближается к нормали поверхности шара. А последняя
равна нормированному вектору радиуса текущей точки. Алгоритм деления проиллюстрируем
рисунком (рис. 6.3).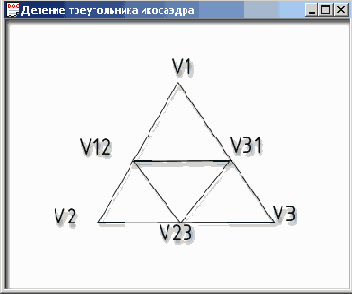
Рис.
6.3. Деление треугольника икосаэдра
Треугольник
с вершинами VI, V2 и V3 разбивается на четыре треугольника: (V1,V12,V31), (V2,V23,V12),
(V3,V32,V23) и (V12.V23.V31). После этого промежуточные точки деления надо посадить
на поверхность шара, то есть изменить их координаты так, чтобы концы векторов
(V12, V23 и V31) дотянулись до поверхности шара. Для этого достаточно нормировать
векторы с помощью уже существующей процедуры Scale. Она впоследствии будет использована
как для масштабирования нормали, так и для нормировки координат вершин новых
треугольников. Но сейчас мы будем вычислять нормаль приближенно. Введем еще
две вспомогательные функции:
//===
Команды OpenGL для изображения одного треугольника
void
setTria(double *vl, double *v2, double *v3)
{
//======
Нормаль и вершина задаются одним вектором
glNormal3dv(vl);
glVertex3dv(vl);
glNormalSdv
(v2);
glVertex3dv(v2);
glNormal3dv(v3);
glVertex3dv(v3);
glEnd()
;
}
//======
Генерация внутренних треугольников
void
Split(double *vl, double *v2, double *v3)
{
//======
Промежуточные вершины
double
v!2[3], v23[3], v31[3);
for
(int l=0; l< 3; i++) {
//======
Можно не делить пополам,
//======
так как будем нормировать
v12[i]
= vl[i]+v2[i];
v23[i]
= v2[i]+v3[i];
v31
[i] = v3[i]+vl [i];
}
//======
Нормируем три новые вершины
Scale(v!2);
Scale(v23);
Scale(v31);
//====== и рисуем четыре треугольника
setTria(vl,
v!2, v31);
setTria
(v2, v23, v!2);
setTria(v3,
v31, v23);
setTria(v!2,v23,
v31);
}
Вставьте эти
глобальные функции в файл и дайте следующую версию функцию DrawScene, в которой
отсутствует вызов функции getNorm для точного вычисления нормали, но есть вызов
функции Split для каждой из 20 граней икосаэдра. В результате мы получаем фигуру
из 80 треугольных граней, которая значительно ближе к сфере, чем икосаэдр:
void
DrawScene()
{
static
double
angle
= 3. * atan(l.)/2.5, V = cos (angle), W = sin (angle),
v[12]
[3] =
{-V,0.,W},
{V,0.,W}, {-V,.0.,-W},
(V,0.,-W),
{0.,W,V}, {0.,W,-V},
(0.,-W,V),
(0.,-W,-V), {W,V,0.},
{-W,V,0.},
{W,-V,0.}, {-W,-V,0.}
};
static
GLuint id[20][3] =
{
(0,1,
4), (0,4, 9), {9,4, 5}, (4,8, 5), (4,1,8),
(8,1,10),
(8,10,3), (5,8, 3), (5,3, 2), (2,3,7),
(7,3,10),
(7,10,6), (7,6,11), (11,6,0), (0,6,1),
(6,10,1),
(9,11,0), (9,2,11), (9,5, 2), (7,11,2)
};
glNewList(l,GL_COMPILE);
glColor3d
(1., 0.4, 1.) ;
glBegin(GLJTRIANGLES);
for
(int i = 0; i < 20; i++)
Split
(v[id[i][0]], v[id[i][l]], v[id[i] [2] ]) ;
glEnd()
;
glEndList
() ;
}
На этой стадии
я рекомендую посмотреть, какие интересные и неожиданные результаты могут быть
получены вследствие ошибок. Все мы ошибаемся, вот и я так долго возился с направлением
обхода и со знаком нормали, что в промежуточных вариантах получал чудовищные
комбинации. Многие из них «канули в Лету», но один любопытный вариант легко
смоделировать. Если ошибки происходят в условиях симметричного отражения, то
возникают ситуации, сходные со случайными изменениями узоров в калейдоскопе.
Замените на обратные знаки компонентов вектора в функции Scale. Это действие
в предыдущих версиях программы было эквивалентно изменению знака нормали. Найдите
строку, похожую на ту, что приведена ниже, и замените знаки так, как показано,
на минусы.
v[0]
/= -d; v[l] /= -d; v[2] /= -d;
|
|